← Ana Rapor / Süreyya Emir MENTEŞ / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 05:15
Bitiş
Devam ediyor
Süre
9 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
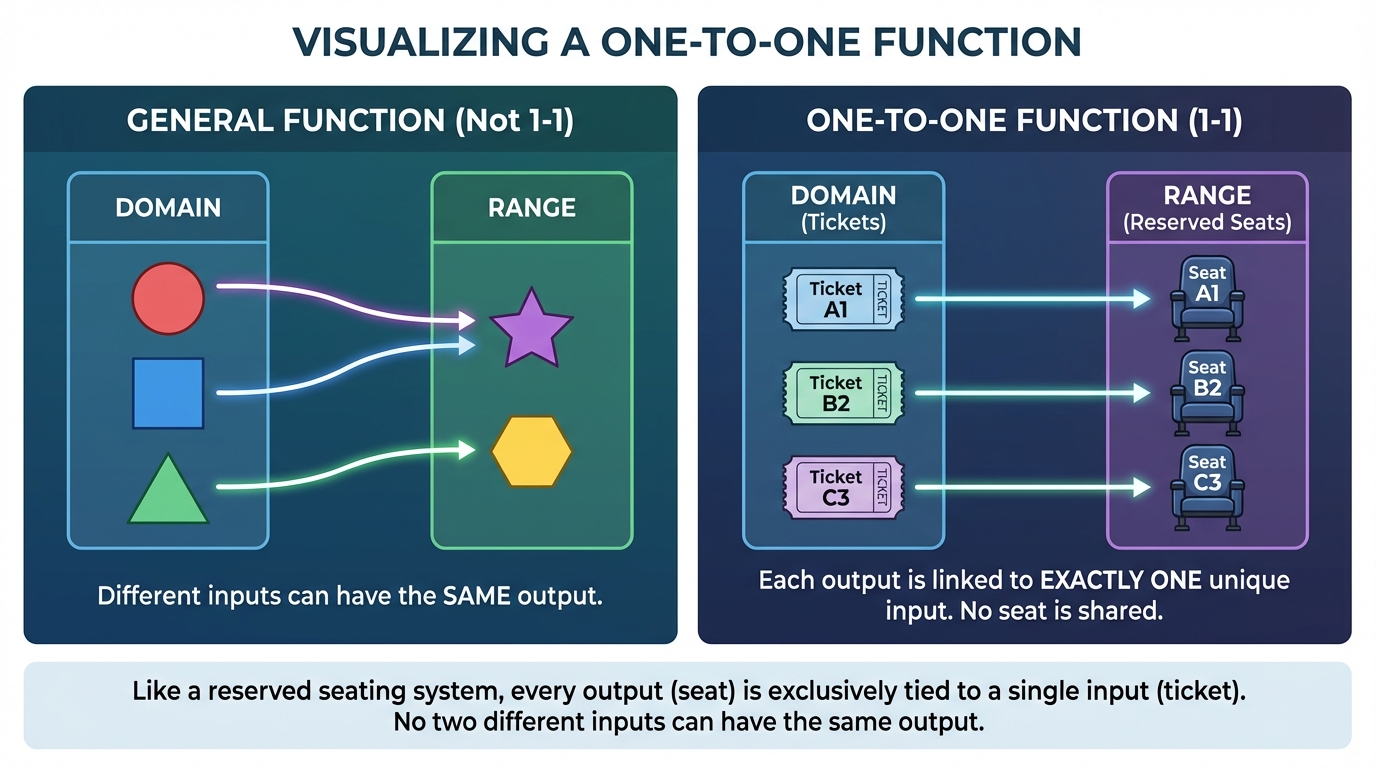
  • 2.1.d. One to One Function

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, "Bire Bir Fonksiyon" (One to One Function) konusunu anlamakta zorluk yaşamıştır. Dersin başında konuyu anladığını belirtmesine rağmen, sorulan ilk soruda bir fonksiyonun "bire bir" olup olmadığını tespit edememiştir. Öğrencinin cevabı, sadece ifadenin bir fonksiyon olduğunu belirtmekle sınırlı kalmış, bire bir olma koşulunu (farklı girdilerin farklı çıktılara sahip olması gerektiği) göz ardı etmiştir. Bu durum, öğrencinin "fonksiyon" tanımı ile "bire bir fonksiyon" tanımını karıştırdığını göstermektedir.

İkinci soruda ise öğrenci, denklemi verilen bir fonksiyonun bire bir olup olmadığını belirlemek için doğrudan bir ipucu istemiştir. Bu, öğrencinin teorik bilgiyi pratik uygulamaya dökme konusunda da eksiklikleri olduğunu ve kendine güveninin düşük olduğunu göstermektedir.

# Güçlü Yönler
Bu derste öğrencinin konuyu tam olarak anladığına dair bir kanıt bulunmamaktadır.

# Geliştirilmesi Gereken Yönler
Öğrencinin "bire bir fonksiyon" tanımını ve bu tanımın nasıl uygulanacağını tekrar etmesi gerekmektedir. Özellikle, farklı girdilerin aynı çıktıya sahip olmasının bire bir olma durumunu nasıl bozduğunu somut örneklerle pekiştirmesi faydalı olacaktır. Hem tanım kümesi-değer kümesi şeklinde verilen fonksiyonlarda hem de cebirsel olarak ifade edilen fonksiyonlarda bire birliği test etme alıştırmaları yapmalıdır.

📜 Oturum Detayları

05:15:15
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
05:15:15
💭 AI Öğretmen
Certainly, preparing explanation now
05:15:15
Görsel
Görsel
05:15:20
AI Öğretmen
A one-to-one function, also called a 1-1 function, is a special kind of function that matches each output value with exactly one input value.
05:15:21
AI Öğretmen
In regular functions, it is possible for two different input values to give the same output value.
05:15:23
AI Öğretmen
But in a one-to-one function, this is not allowed, because each output must come from only one input.
05:15:25
AI Öğretmen
You can think of it like a reserved seating system in a movie theater.
05:15:27
AI Öğretmen
Each ticket is for one specific seat, and you can't have two tickets that both claim the same seat.
05:15:29
AI Öğretmen
In the world of functions, this means that every output is linked to just one input, and no output is shared between inputs.
05:15:31
AI Öğretmen
So, every element in the range (which are the output values a function gives) can only be matched to at most one thing from the domain (the input values you start with).
05:15:32
AI Öğretmen
Did you understand how a one-to-one function ensures each output corresponds to a unique input?
05:20:06
Öğrenci
I got it
05:20:08
💭 AI Öğretmen
Let us proceed then
05:20:08
❓ Soru basic
Determine whether the following function is one-to-one: ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_185ba90c-a01e-449e-9b2f-98a502915e79.png)
05:20:39
Öğrenci
My answer is: This is a function
05:20:39
💭 AI Öğretmen
Noted your response
05:20:43
AI Öğretmen
Your answer was not correct, let me explain why. The question asks if the function is one-to-one, but you only said it is a function without checking if it meets the one-to-one condition.
05:20:46
AI Öğretmen
A one-to-one function means that each input in the domain connects to a unique output in the codomain, so no two different inputs share the same output.
05:20:47
AI Öğretmen
In the given function, both inputs "b" and "c" point to the same output "y," which means two different inputs give the same output. This shows the function is not one-to-one.
05:20:49
AI Öğretmen
A common misconception is thinking that just being a function means it is one-to-one, but the key is to check if outputs repeat for different inputs.
05:20:51
AI Öğretmen
For example, if "a" maps to "x" and "b" maps to "x" as well, the function would not be one-to-one because "x" has two arrows pointing to it.
05:20:52
AI Öğretmen
Therefore, the correct answer should be: The function is not one-to-one.
05:20:52
AI Öğretmen
Should we continue with the lecture?
05:21:37
Öğrenci
Alright, let's continue
05:21:38
💭 AI Öğretmen
Continuing shortly
05:21:44
🎥 Video
05:21:45
AI Öğretmen
Did you understand how a one-to-one function works?
05:22:12
Öğrenci
I got it
05:22:15
💭 AI Öğretmen
Let us review this point.
05:22:15
❓ Soru basic
**Example:** Determine whether the function $f: \mathbb{R} \to \mathbb{R}, f(x) = 5x - 9$ is one to one or not. Explain your reasoning.
05:24:19
Öğrenci
Can you give me a hint, teacher?
05:24:20
💭 AI Öğretmen
Let me consider that
05:24:29
AI Öğretmen
What do you think would happen if you took two different input values and plugged them into the function? Would their outputs be the same or different?
05:24:30
AI Öğretmen
How could you use the equation \( f(x) = 5x - 9 \) to test whether different inputs can produce the same output?
05:24:33
AI Öğretmen
If you set \( f(x_1) = f(x_2) \) for two inputs \( x_1 \) and \( x_2 \), what would that tell you about the relationship between \( x_1 \) and \( x_2 \)?

Voltran Okul Analiz Sistemi