← Ana Rapor / Ayşe TATLI / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:28
Bitiş
02 December 2025, 06:51
Süre
23 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
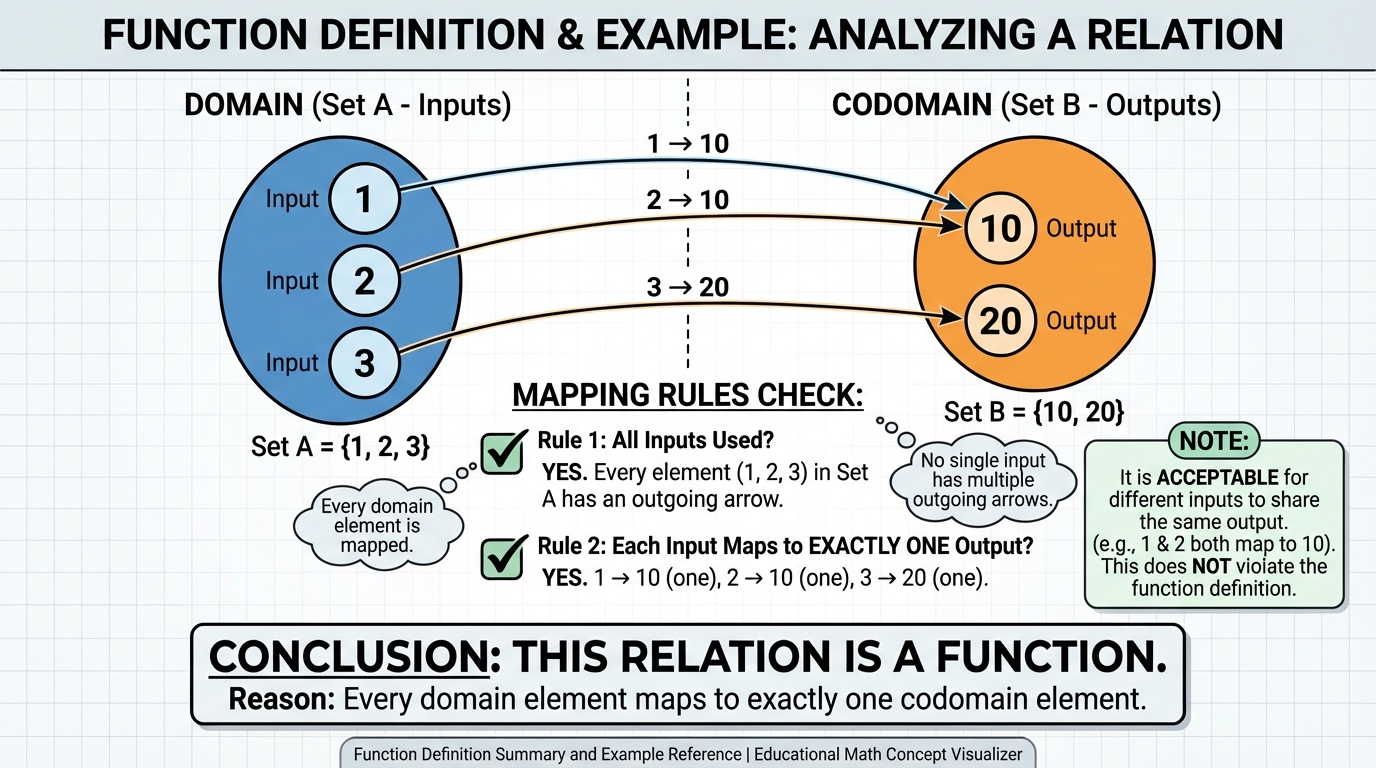
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, fonksiyonların pratik uygulamalarında (tanım kümesi bulma, değer hesaplama) başarılı bir performans sergilemiştir. Özellikle rasyonel bir fonksiyonun en geniş tanım kümesini doğru bir şekilde belirlemiş ve karmaşık bir fonksiyon ifadesinin değerini doğru hesaplamıştır. Bu, öğrencinin işlem becerisinin ve temel fonksiyon mekaniklerini anladığının bir göstergesidir.

Ancak, bir bağıntının "fonksiyon" olup olmadığını belirleyen temel kural konusunda ciddi bir kavramsal eksikliği bulunmaktadır. Özellikle, tanım ve değer kümelerinin (doğal sayılar gibi) kısıtlayıcı olduğu durumlarda, bir bağıntının fonksiyon olma şartlarını uygulamakta zorlanmıştır. Bu konudaki soruya önce ipucu istemiş, ardından verdiği ilgisiz cevapla konunun özünü (her tanım kümesi elemanının görüntüsünün değer kümesinde olması gerektiği) anlamadığını göstermiştir.

Öğrencinin İyi Olduğu Konular

Öğrenci, aşağıdaki konularda başarılı olmuştur:
* Bir fonksiyonun tanım, değer ve görüntü kümelerini verilen bir şemadan doğru bir şekilde belirleme.
* Rasyonel bir ifadenin paydasını sıfır yapan değeri bularak fonksiyonun en geniş tanım kümesini doğru bir şekilde tespit etme.
* Verilen bir `f(x-1)` gibi bir ifadede, istenen `f(3)` değerini bulmak için doğru `x` değerini hesaplayıp yerine koyma.

Geliştirilmesi Gereken Konular

Öğrencinin en belirgin eksiği, bir bağıntının fonksiyon olup olmadığını belirleyen kuralları anlama ve uygulama noktasındadır.
* Fonksiyon Olma Şartları: Öğrenci, bir fonksiyonda tanım kümesindeki her elemanın çıktısının mutlaka değer kümesi içinde yer alması gerektiği kuralını gözden kaçırmıştır. `f(x) = x - 3` fonksiyonunun N'den N'ye bir fonksiyon olmadığını, çünkü `x=1` için çıktının `-2` olup doğal sayılar kümesinde yer almadığını kavrayamamıştır. Bu, fonksiyonun temel tanımında bir eksiklik olduğunu göstermektedir.

Ders Dışı Yorumlar

Ders sırasında konu dışı herhangi bir soru veya yorum kaydedilmemiştir.

📜 Oturum Detayları

06:28:15
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:28:15
💭 AI Öğretmen
Preparing the detailed explanation
06:28:15
🎥 Video
06:28:16
AI Öğretmen
Did you understand how a function maps each element from Set A to exactly one element in Set B?
06:28:52
Öğrenci
I got it
06:28:54
💭 AI Öğretmen
Alright, moving forward
06:28:55
🎥 Video
06:28:56
AI Öğretmen
Did you understand how the domain, codomain, and range relate to each other in a function?
06:29:35
Öğrenci
I got it
06:29:37
💭 AI Öğretmen
Let us review this question next
06:29:38
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:31:42
Öğrenci
My answer is: Domain: -1,0,1,2 Codomain: 0,1,2,3,4,5 Range: 0,1,4
06:31:43
💭 AI Öğretmen
Reviewing your answer now
06:31:49
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range of the function.
06:31:52
AI Öğretmen
You clearly understand that the domain is all possible inputs, the codomain is all possible outputs, and the range is the set of actual outputs that the function produces.
06:31:52
AI Öğretmen
This shows a great grasp of fundamental function concepts! Keep up the excellent work!
06:31:53
AI Öğretmen
Should we continue with the lecture?
06:32:14
Öğrenci
Alright, let's continue
06:32:15
💭 AI Öğretmen
Moving forward now
06:32:20
Görsel
Görsel
06:32:23
AI Öğretmen
A relation can be considered a function if it follows an important rule.
06:32:25
AI Öğretmen
This rule is that every input, which is an element from the domain or Set A, must be paired with some output in the codomain, also called Set B.
06:32:28
AI Öğretmen
It’s also good to remember that not every element in Set B has to be used, so some elements in the codomain might not be matched to any input.
06:32:30
AI Öğretmen
It’s okay if different inputs in Set A lead to the same output in Set B; this is called a many-to-one relationship.
06:32:32
AI Öğretmen
However, one input cannot be matched to more than one output in the codomain, so one-to-many relationships are not allowed in functions.
06:32:34
AI Öğretmen
So, a function always assigns exactly one output in the codomain to each input from the domain.
06:32:34
AI Öğretmen
Did you understand how a relation qualifies as a function based on the input-output rules?
06:33:15
Öğrenci
I got it
06:33:17
💭 AI Öğretmen
Let us review this concept
06:33:18
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:34:04
Öğrenci
Can you give me a hint, teacher?
06:34:06
💭 AI Öğretmen
Let me consider that
06:34:07
AI Öğretmen
What values does the function produce when you input the smallest numbers in the domain, like 0, 1, or 2?
06:34:08
AI Öğretmen
How do these output values compare to the codomain, which is the set of natural numbers?
06:34:10
AI Öğretmen
Can a function from natural numbers to natural numbers produce outputs outside the natural numbers? What does this mean for the function's definition?
06:38:08
Öğrenci
My answer is: R: all real numbers except -3
06:38:09
💭 AI Öğretmen
Let me review that answer
06:38:14
AI Öğretmen
Your answer was not correct, let me explain why the relation \( f(x) = x - 3 \) from \(\mathbb{N}\) to \(\mathbb{N}\) is not a function.
06:38:17
AI Öğretmen
A function from \(\mathbb{N}\) to \(\mathbb{N}\) must assign a natural number output for every natural number input in the domain. Here, when you plug in \(x=1\), you get \(f(1) = 1 - 3 = -2\), which is not a natural number.
06:38:19
AI Öğretmen
This means that \(f\) does not produce outputs in the codomain \(\mathbb{N}\) for all inputs, so it fails the definition of a function on this domain and codomain.
06:38:21
AI Öğretmen
A common misconception is mixing the domain or codomain with real numbers or misunderstanding the set \(\mathbb{N}\) (natural numbers include only positive integers like 1, 2, 3, ...).
06:38:23
AI Öğretmen
For example, if \(f(x) = x + 1\), then for any natural number input, the output is also a natural number, so that would be a function from \(\mathbb{N}\) to \(\mathbb{N}\).
06:38:24
AI Öğretmen
Therefore, the correct answer should be: No, it is not a function.
06:38:25
AI Öğretmen
Should we continue with the lecture?
06:39:30
Öğrenci
Alright, let's continue
06:39:31
💭 AI Öğretmen
Moving forward now
06:39:39
Görsel
Görsel
06:39:43
AI Öğretmen
A relation shows how elements from one set (called the domain or input set) are connected to elements in another set (called the codomain or output set).
06:39:44
AI Öğretmen
To check if a relation is a function, we need to make sure that each element from the input set is paired with only one element from the output set.
06:39:46
AI Öğretmen
Let’s look at two sets: Set A is the input set with elements $\{1, 2, 3\}$, and Set B is the output set with elements $\{10, 20\}$.
06:39:48
AI Öğretmen
The pairs for the relation are: $1 \to 10$, $2 \to 10$, $3 \to 20$.
06:39:49
AI Öğretmen
Every input ($1$, $2$, and $3$) from Set A is used, and each is matched with just one value in Set B.
06:39:50
AI Öğretmen
It is okay that both $1$ and $2$ map to $10$, because each input still goes to only one output.
06:39:51
AI Öğretmen
Because each item from the input set has one matching output, this relation is a function.
06:39:52
AI Öğretmen
Did you understand why this relation qualifies as a function?
06:40:41
Öğrenci
I got it
06:40:44
💭 AI Öğretmen
Let us reinforce this concept.
06:40:44
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:45:15
Öğrenci
My answer is: all real numbers subtracted by -2
06:45:16
💭 AI Öğretmen
Let me consider that answer
06:45:25
AI Öğretmen
Fantastic job! You've absolutely nailed it!
06:45:27
AI Öğretmen
You correctly identified that the denominator of a fraction cannot be zero, which is the key restriction for rational functions like this one.
06:45:27
AI Öğretmen
This shows a great understanding of how to find the domain by ensuring the function is always defined. Keep up the excellent work!
06:45:28
AI Öğretmen
Therefore, the correct answer is all real numbers except -2.
06:45:29
AI Öğretmen
Should we continue with the lecture?
06:45:59
Öğrenci
Alright, let's continue
06:46:00
💭 AI Öğretmen
Moving to next section
06:46:07
AI Öğretmen
A relation can be called a function only when every input from the domain has exactly one output in the codomain.
06:46:09
AI Öğretmen
This means that each starting value, or input, links to only one ending value, or output.
06:46:10
AI Öğretmen
It's okay if more than one input has the same output, but one input cannot have two or more different outputs.
06:46:12
AI Öğretmen
As long as every input matches with only one output, the rule is a function, even if some outputs are shared.
06:46:13
AI Öğretmen
Does the idea that each input must have exactly one output make sense to you?
06:46:40
Öğrenci
Can one output be linked to multiple inputs in a function?
06:46:42
💭 AI Öğretmen
Let me consider that
06:46:46
AI Öğretmen
Yes, in a function, one output can be linked to multiple inputs. This is called a many-to-one relationship and it is allowed because the rule only requires that each input has exactly one output, not that outputs must be unique.
06:46:47
AI Öğretmen
Did that answer your question clearly?
06:47:06
Öğrenci
I got it
06:47:08
💭 AI Öğretmen
Let's reinforce this concept
06:47:09
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:49:42
Öğrenci
My answer is: x-1=3, x=4 4x4 +2= 18
06:49:44
💭 AI Öğretmen
Let me verify that now
06:49:49
AI Öğretmen
That's absolutely right! Fantastic job!
06:49:50
AI Öğretmen
You correctly set $x-1$ equal to 3 to find the value of $x$ that makes the argument 3.
06:49:51
AI Öğretmen
Then you perfectly substituted that $x$ value into the function's expression to get the correct result.
06:49:52
AI Öğretmen
This shows a great understanding of how to evaluate functions by finding the correct input value!
06:49:53
AI Öğretmen
Therefore the correct answer is 18.
06:49:53
AI Öğretmen
Should we continue with the lecture?
06:50:20
Öğrenci
Alright, let's continue
06:50:21
💭 AI Öğretmen
Preparing the next explanation
06:50:31
AI Öğretmen
In this lesson, we learned that a function is a special type of relation where every input from the domain is paired with exactly one output in the codomain. We discussed the concepts of domain, codomain, and range, and clarified that while multiple inputs can share the same output, one input cannot have multiple outputs. We also looked at examples to identify whether relations are functions based on these rules. Do you have any questions about these concepts? If not, we can wrap up the lesson here.
06:51:18
Öğrenci
Anladım hocam.
06:51:25
AI Öğretmen
See you in the next lesson!

Voltran Okul Analiz Sistemi