← Ana Rapor / Ali Raşit ÖZKAN / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:28
Bitiş
02 December 2025, 06:45
Süre
18 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
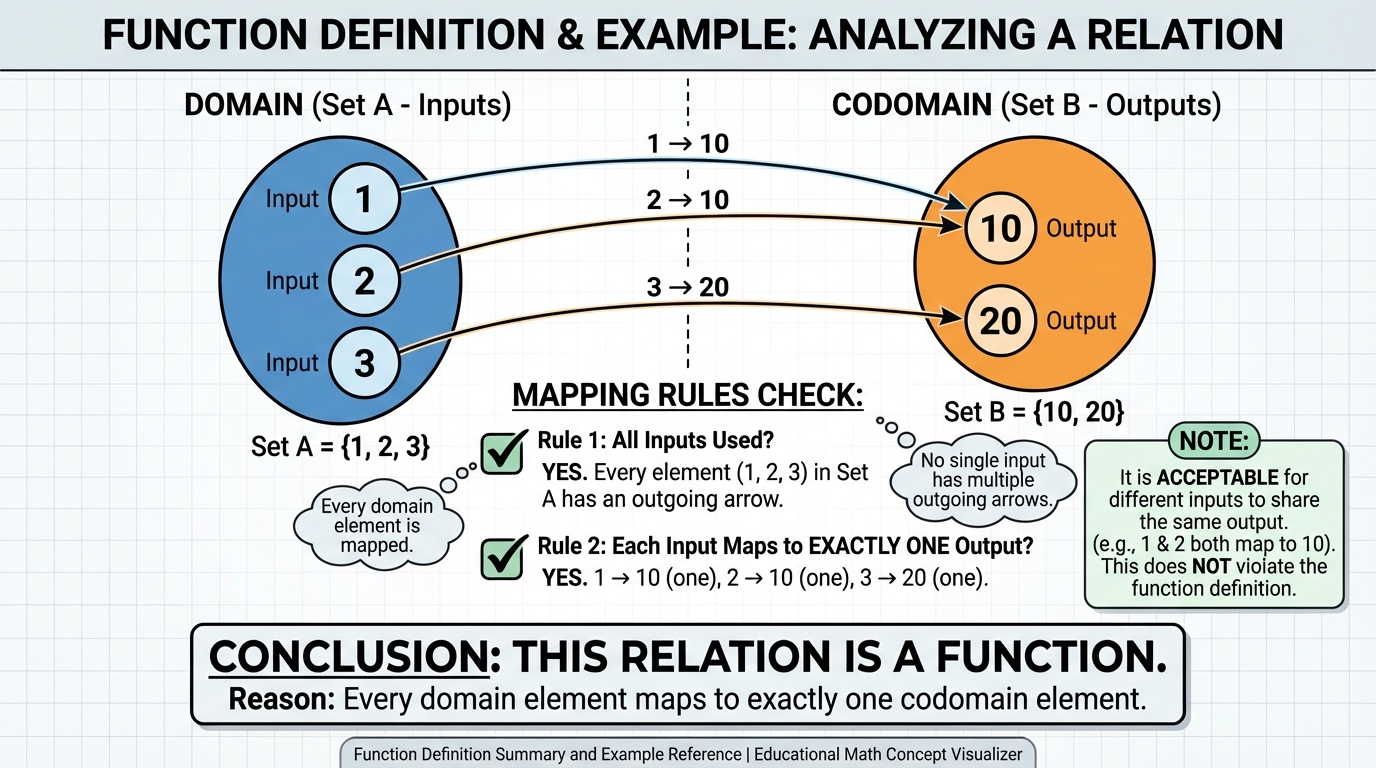
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, fonksiyonların temel tanımı konusunda karma bir performans sergilemiştir. Dersin başında tanım, tanım kümesi (domain), değer kümesi (codomain) ve görüntü kümesi (range) gibi temel kavramlar hakkında açıklama istemiş ve bu kavramları anladığını belirtmiştir.

Başarılı Olduğu Alanlar:
- Kendisine tanım ve değer kümeleri verildiğinde, bu kümeler üzerinden görüntü kümesini doğru bir şekilde tespit edebilmiştir.
- Bir bağıntının, belirtilen tanım ve değer kümeleri (doğal sayılardan doğal sayılara) dahilinde fonksiyon olup olmadığını doğru bir şekilde analiz edebilmiştir.
- Fonksiyonel ifadelerde değer bulma (örneğin, f(x-1) verildiğinde f(3)'ü bulma) konusunda başarılı olmuştur.

Geliştirilmesi Gereken Alanlar:
- En önemli eksikliği, bir fonksiyonun en geniş tanım kümesini bulma konusunda yaşanmıştır. Rasyonel bir ifadenin paydasını sıfır yapan değeri doğru tespit etmesine rağmen, tanım kümesini "bu değer dışındaki tüm reel sayılar" olarak ifade edememiştir. Bu durum, tanım kümesini yazma ve ifade etme konusunda bir eksiklik olduğunu göstermektedir.
- Dersin başında, görüntü kümesinin nasıl bulunacağına dair doğrudan bir soru sorması, bu kavramın başlangıçta tam oturmadığını göstermektedir.

Öğrenci genel olarak konuya ilgili ve soruları doğru cevaplama eğiliminde olsa da, özellikle en geniş tanım kümesini belirleme gibi kritik bir kazanımda zorlanması, konunun temelinde bazı boşluklar olduğunu düşündürmektedir.

📜 Oturum Detayları

06:28:17
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:28:18
💭 AI Öğretmen
Getting everything set up
06:28:18
🎥 Video
06:28:19
AI Öğretmen
Did you understand how a function assigns exactly one output to each input?
06:28:58
Öğrenci
I got it
06:29:01
💭 AI Öğretmen
Let us continue then
06:29:01
🎥 Video
06:29:02
AI Öğretmen
Did this explanation about domain, codomain, and range make sense to you?
06:29:45
Öğrenci
How do you find the range of a function from its domain and codomain?
06:29:48
💭 AI Öğretmen
Let me review that concept
06:29:53
AI Öğretmen
To find the range of a function, you look at all the outputs the function actually produces from every input in the domain. You apply the function rule to each input and collect the resulting values—these collected values form the range. So, the range is the set of all outputs that the function hits, which is always a subset of the codomain. Does this explanation help you understand how to find the range?
06:30:20
Öğrenci
I got it
06:30:22
💭 AI Öğretmen
Let us proceed then
06:30:22
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:32:01
Öğrenci
My answer is: Domain:-1,0,1,2 Codomain:0,1,2,3,4,5 Range:0,1,4
06:32:02
💭 AI Öğretmen
Let me review that answer
06:32:07
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range for the function.
06:32:10
AI Öğretmen
You clearly understand that the domain is all possible inputs, the codomain is all possible outputs, and the range is the set of actual outputs that are used.
06:32:11
AI Öğretmen
Keep up the great work!
06:32:14
AI Öğretmen
Therefore the correct answer is Domain: $\{-1, 0, 1, 2\}$, Codomain: $\{0, 1, 2, 3, 4, 5\}$, Range: $\{0, 1, 4\}$
06:32:14
AI Öğretmen
Should we continue with the lecture?
06:32:40
Öğrenci
Alright, let's continue
06:32:41
💭 AI Öğretmen
Moving forward now
06:32:46
Görsel
Görsel
06:32:48
AI Öğretmen
A relation is called a function if it follows a special rule.
06:32:51
AI Öğretmen
This rule says that every input from the Domain, also known as Set A, must be matched to some output in the Codomain, which is Set B.
06:32:53
AI Öğretmen
In simple terms, each input gets connected to an output, and there are no inputs left without an output.
06:32:55
AI Öğretmen
However, not every element in Codomain (Set B) needs to be used, so there can be outputs that aren't matched to any input.
06:32:57
AI Öğretmen
It is also allowed for different inputs to share the same output, which we call many-to-one mappings.
06:32:59
AI Öğretmen
But it is not allowed for one input to connect to more than one output, so one-to-many mappings cannot happen in a function.
06:33:00
AI Öğretmen
A function always gives exactly one output for each input in the domain.
06:33:01
AI Öğretmen
Did you understand how to determine if a relation is a function based on the rules we discussed?
06:33:43
Öğrenci
I got it
06:33:45
💭 AI Öğretmen
Let us proceed carefully
06:33:45
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:36:17
Öğrenci
My answer is: No its not domain because -2-3 its not function
06:36:17
💭 AI Öğretmen
Let me review that carefully
06:36:23
AI Öğretmen
That's absolutely right! Fantastic job!
06:36:25
AI Öğretmen
You correctly identified that this relation is not a function because when you input natural numbers like 1 or 2, the output (like -2 or -1) is not a natural number.
06:36:26
AI Öğretmen
A key concept here is that for a relation to be a function, every element in the domain must map to an element *within* the specified codomain.
06:36:27
AI Öğretmen
You've clearly grasped the definition of a function and how domains and codomains work!
06:36:28
AI Öğretmen
Therefore, the correct answer is No.
06:36:28
AI Öğretmen
Should we continue with the lecture?
06:36:55
Öğrenci
Alright, let's continue
06:36:55
💭 AI Öğretmen
Moving on now
06:37:01
Görsel
Görsel
06:37:05
AI Öğretmen
A relation between two sets can be checked to see if it is a function by looking at some rules.
06:37:06
AI Öğretmen
Let's look at two sets: Set A is the inputs, which are $\{1, 2, 3\}$, and Set B is the outputs, which are $\{10, 20\}$.
06:37:07
AI Öğretmen
The mapping pairs are: $1 \to 10$, $2 \to 10$, $3 \to 20$.
06:37:09
AI Öğretmen
That means 1 is matched to 10, 2 to 10, and 3 to 20.
06:37:10
AI Öğretmen
All the inputs, 1, 2, and 3, are used in these mappings.
06:37:11
AI Öğretmen
Each input from Set A is paired with only one output in Set B.
06:37:12
AI Öğretmen
It's okay for different inputs (like 1 and 2) to have the same output (10).
06:37:13
AI Öğretmen
So, this relation is a function because every input has exactly one output.
06:37:14
AI Öğretmen
Did you understand how to determine if a relation is a function based on the example given?
06:37:49
Öğrenci
I got it
06:37:52
💭 AI Öğretmen
Let us proceed carefully
06:37:52
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:40:01
Öğrenci
My answer is: Ifb -2+2=0 this shows 4/0 is undifined
06:40:03
💭 AI Öğretmen
Noted your explanation
06:40:07
AI Öğretmen
Your answer was not fully correct because you identified the restriction correctly but did not clearly state the largest domain of the function.
06:40:09
AI Öğretmen
The function \( f(x) = \frac{4}{x+2} \) is undefined when the denominator is zero, which happens at \( x = -2 \). So, the domain is all real numbers except \( -2 \).
06:40:12
AI Öğretmen
To find the domain step-by-step: 1) Look at the denominator \( x+2 \). 2) Set it not equal to zero: \( x+2 \neq 0 \). 3) Solve for \( x \): \( x \neq -2 \). This means the function works for every number except \( -2 \).
06:40:14
AI Öğretmen
A common misconception is to only find the value that makes the denominator zero but not express the domain clearly as all other values except that. For example, the domain could be written as \( \{ x \in \mathbb{R} \mid x \neq -2 \} \) or in interval notation as \( (-\infty, -2) \cup (-2, \infty) \).
06:40:16
AI Öğretmen
Therefore, the correct answer should be the set of all real numbers except \( -2 \), expressed as \( \{ x \in \mathbb{R} \mid x \neq -2 \} \).
06:40:16
AI Öğretmen
Should we continue with the lecture?
06:41:23
Öğrenci
Alright, let's continue
06:41:24
💭 AI Öğretmen
Moving forward now
06:41:33
AI Öğretmen
A relation is considered a function when every input value from the domain is matched with one and only one output value in the codomain.
06:41:34
AI Öğretmen
This means that for each input, there can be no confusion or choice—every input leads to just one output.
06:41:35
AI Öğretmen
It's also okay if different inputs are paired with the same output; what matters is that each input only gets assigned to one output.
06:41:37
AI Öğretmen
So, although outputs can be shared by multiple inputs, an input can never be mapped to more than one output if the relation is going to be a function.
06:41:38
AI Öğretmen
Does this explanation make sense to you?
06:42:14
Öğrenci
I got it
06:42:18
💭 AI Öğretmen
Now, let's review this carefully
06:42:18
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:43:46
Öğrenci
My answer is: 16+2=18
06:43:47
💭 AI Öğretmen
Let me confirm that
06:43:50
AI Öğretmen
That's absolutely right! Fantastic job!
06:43:52
AI Öğretmen
You correctly figured out that once you substitute x=4 into the expression, you get 16 + 2, which equals 18.
06:43:53
AI Öğretmen
You clearly understood the key step of setting $x-1$ equal to 3 to find the correct 'x' value to substitute into the function. Keep up the great work!
06:43:55
AI Öğretmen
Therefore the correct answer is 18.
06:43:55
AI Öğretmen
Should we continue with the lecture?
06:44:18
Öğrenci
Alright, let's continue
06:44:19
💭 AI Öğretmen
Preparing next part
06:44:28
AI Öğretmen
In this lesson, we covered the definition of a function as a relation where every input from the domain maps to exactly one output in the codomain. We also discussed the concepts of domain, codomain, and range, and how to determine if a relation is a function by checking that each input has a unique output. An example was given to illustrate these ideas. Do you have any questions about these topics? If not, I’ll end the lesson.
06:45:55
Öğrenci
finish lesson
06:45:59
AI Öğretmen
See you in the next lesson!

Voltran Okul Analiz Sistemi