← Ana Rapor / Şadiye Derin ULUSOY / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:43
Bitiş
Devam ediyor
Süre
12 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
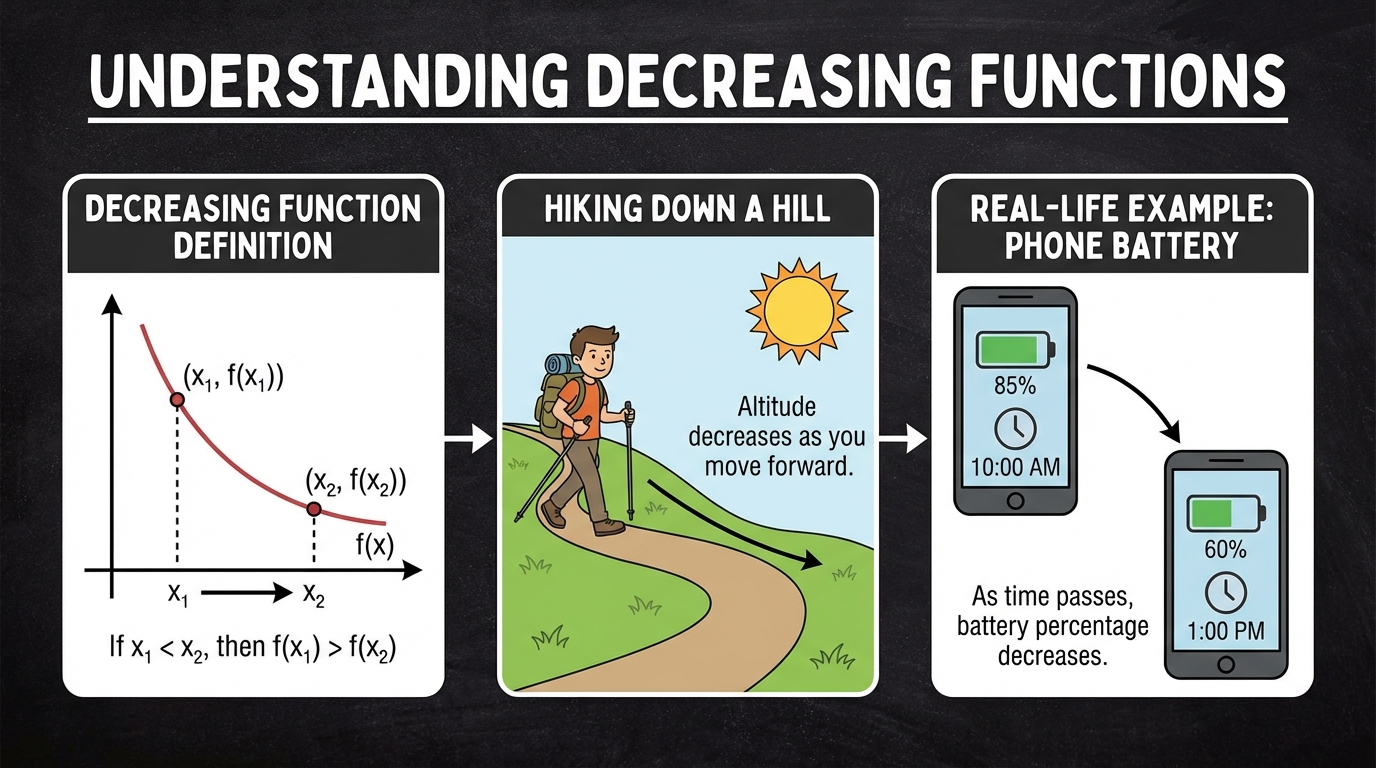
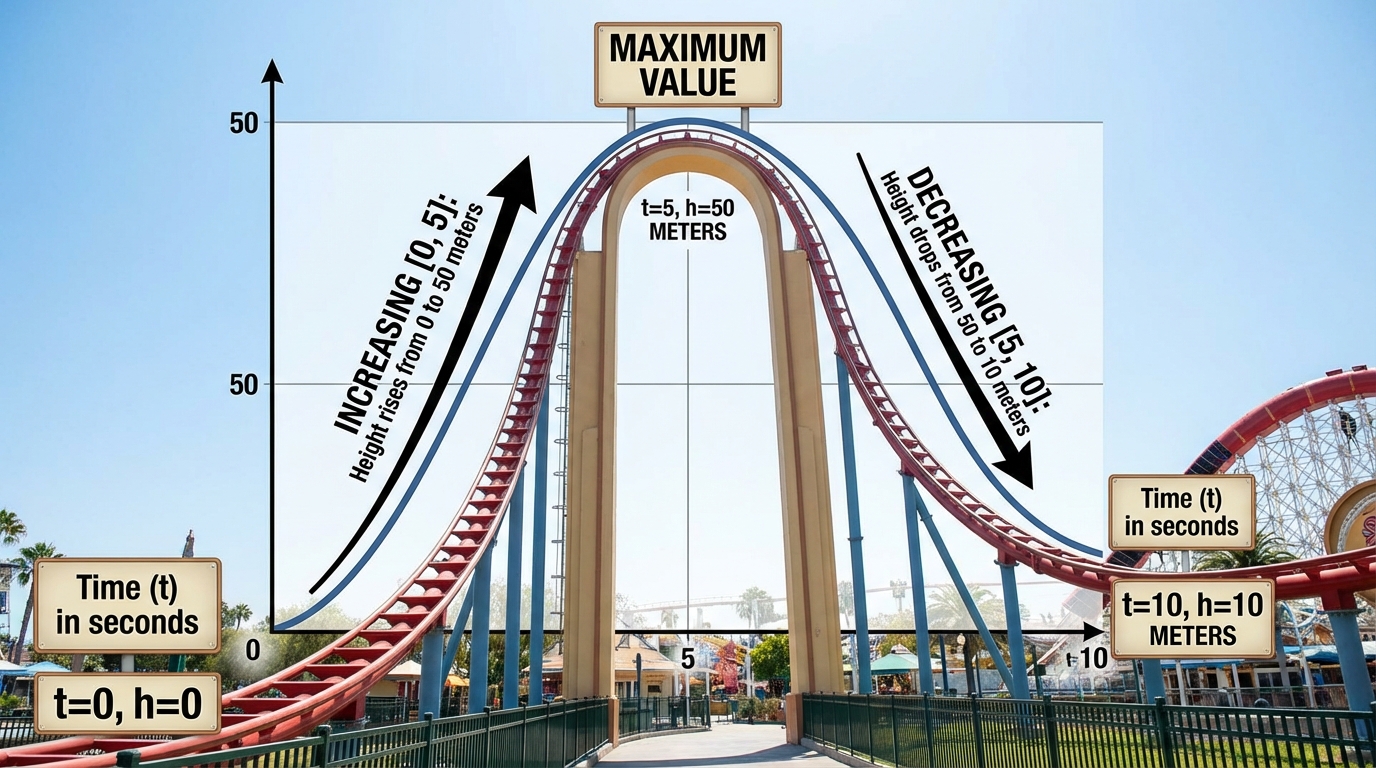
  • 2.1.c. Increasing and Decreasing Intervals of a Function

Detaylı Değerlendirme

Genel Değerlendirme
Öğrenci, bir fonksiyonun grafiğini soldan sağa okuyarak artan ve azalan aralıkları belirleme temel mantığını kavramış görünüyor. Artan aralıkları ve fonksiyonun maksimum değerini bulma konusunda başarılıdır. Ancak, azalan aralığı belirtirken kullandığı parantez (açık aralık) hatası, aralık tanımının (kapalı aralık dahil) tam olarak anlaşılmadığını göstermektedir.

Öğrenci Analizi
- Anlama Seviyesi: Öğrenci, konuların görsel yorumlamasında genel olarak başarılı. Artan aralıkları ve bir fonksiyonun tepe noktasını (maksimum değer) grafikten okuyabiliyor.
- Zorlandığı Noktalar: En belirgin zorluk, bir fonksiyonun azaldığı aralığı tanımlarken doğru aralık notasını (köşeli parantez `[]` kullanımı) kullanma konusunda yaşanmıştır. Öğrenci, aralığı doğru tespit etse de açık aralık `()` kullanmıştır, bu da aralığın uç noktalarının tanıma dahil olup olmadığı konusunda bir kavram yanılgısına işaret etmektedir.
- Öğrenme Hızı: Kavramları hızlıca anladığını belirtiyor ("I got it") ve basit sorularda başarılı oluyor, ancak notasyon gibi teknik detaylarda eksiklikleri var.

Konu Bazlı Analiz

# İyi Olduğu Konular
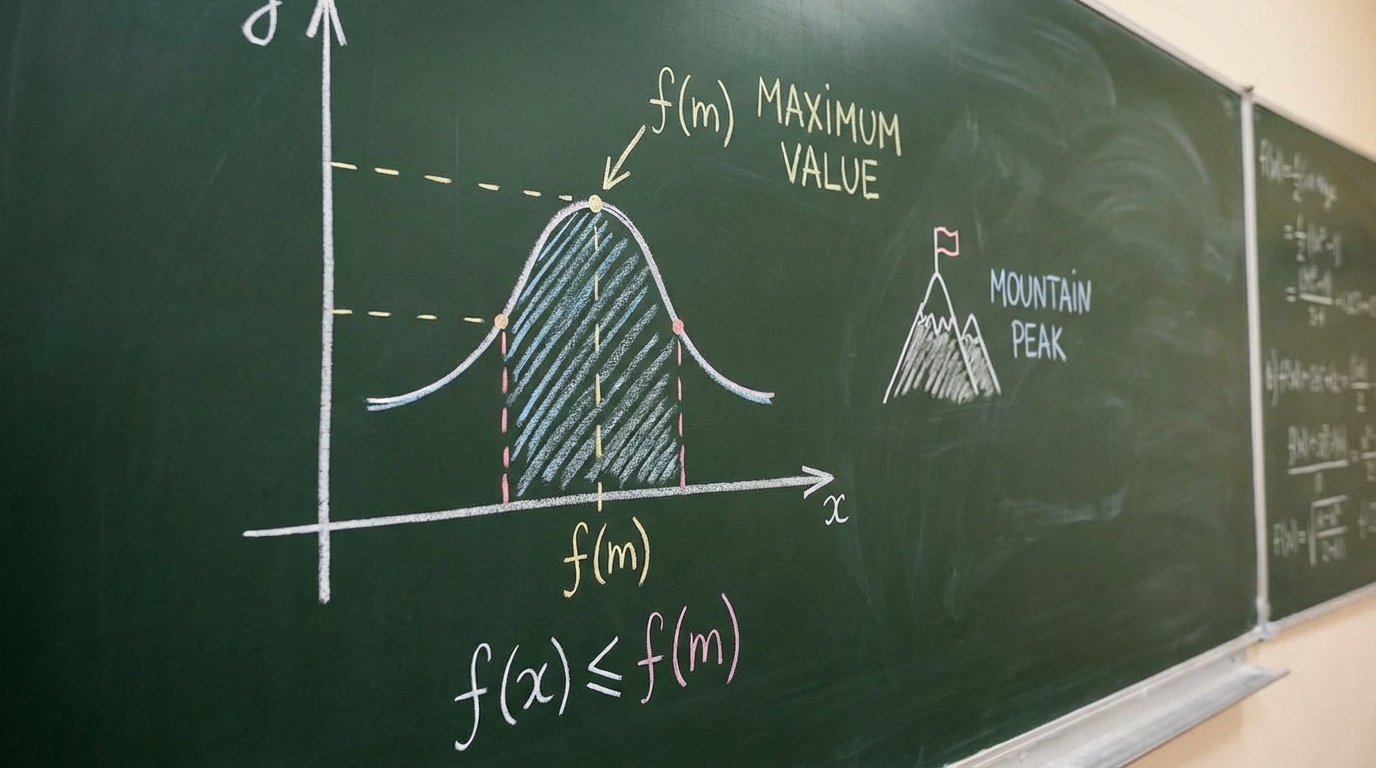
Öğrenci, bir fonksiyonun grafiğindeki temel özellikleri okuma konusunda yeteneklidir. Özellikle, fonksiyonun arttığı kısımları ve en yüksek noktayı (maksimum değer) doğru bir şekilde tespit etmiştir.

# Eksik Olduğu Konular
Öğrencinin temel eksiği, artan ve azalan aralıkların tanımının teknik detaylarındadır. Özellikle bir aralığın uç noktalarının (endpoints) ne zaman aralığa dahil edileceğini (kapalı aralık) ve bu durumun matematiksel notasyonla nasıl gösterileceğini tam olarak anlamamıştır. Azalan aralık sorusuna `(-2,0)` yerine `[-2,0]` cevabını vermesi gerekirken yaptığı hata bu eksikliği açıkça göstermektedir.

📜 Oturum Detayları

06:43:59
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:44:00
💭 AI Öğretmen
Let me begin the explanation
06:44:00
Görsel
Görsel
06:44:03
AI Öğretmen
Graphs in mathematics are always read from left to right, just like reading a sentence in English.
06:44:04
AI Öğretmen
This way of looking at graphs helps us understand how a function changes as we move along the $x$-axis.
06:44:05
AI Öğretmen
When we talk about two $x$-values, we look at what happens between them as we go from left to right.
06:44:06
AI Öğretmen
By paying attention to this left-to-right direction, we can tell if the function is going up or down between those points.
06:44:08
AI Öğretmen
Remembering to read graphs from left to right makes it easier to figure out where a function is increasing or decreasing.
06:44:10
AI Öğretmen
Did you follow how reading the graph from left to right helps us understand increasing and decreasing intervals?
06:44:42
Öğrenci
I got it
06:44:44
💭 AI Öğretmen
Let us continue now
06:44:44
🎥 Video
06:44:45
AI Öğretmen
Did you understand what it means for a function to be increasing on an interval?
06:45:27
Öğrenci
I got it
06:45:30
💭 AI Öğretmen
Let us proceed now
06:45:30
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_33e16c0c-dc3a-47bd-91c9-e1d47eecd95c.png) Example: The graph of f is shown on the below. Find the intervals of x for which f(x) is **increasing**.
06:47:35
Öğrenci
My answer is: increasing: (-5,-2 ) union(0,3)
06:47:35
💭 AI Öğretmen
Thank you for your answer
06:47:40
AI Öğretmen
Fantastic job! That's absolutely right!
06:47:41
AI Öğretmen
You correctly identified the intervals where the graph of the function is moving upwards as you read it from left to right.
06:47:43
AI Öğretmen
This means that as the x-values increase, the corresponding y-values are also increasing, which is the definition of an increasing function.
06:47:44
AI Öğretmen
Your answer, (-5,-2 ) union(0,3), perfectly captures where the function is on the rise!
06:47:45
AI Öğretmen
Should we continue with the lecture?
06:48:13
Öğrenci
Alright, let's continue
06:48:14
💭 AI Öğretmen
Moving forward now
06:48:18
Görsel
Görsel
06:48:21
AI Öğretmen
A function is called decreasing on an interval when, if you pick any two numbers where $x_1$ is less than $x_2$, the value of the function at $x_1$, written as $f(x_1)$, is greater than $f(x_2)$.
06:48:23
AI Öğretmen
You can think about walking down a hill.
06:48:24
AI Öğretmen
As you walk forward, your height gets lower, just like a function’s value goes down as you pick bigger $x$ numbers.
06:48:27
AI Öğretmen
Another example is your phone’s battery during the day.
06:48:28
AI Öğretmen
As time moves on, the battery percentage usually drops, showing how a real-life decreasing function works.
06:48:28
AI Öğretmen
Does the idea of a decreasing function make sense to you so far?
06:48:56
Öğrenci
I got it
06:48:58
💭 AI Öğretmen
Now, let's review this question
06:48:59
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_fb69fa74-e294-4d91-a021-e549025bd3c4.png) Example: The graph of $f$ is shown on the above. Find the intervals of $x$ for which $f(x)$ is **decreasing**.
06:49:52
Öğrenci
My answer is: decreasing: (-2,0)
06:49:53
💭 AI Öğretmen
Noted your answer
06:49:57
AI Öğretmen
Your answer was not correct, let me explain why the interval should include the endpoints -2 and 0.
06:49:58
AI Öğretmen
A function is decreasing on an interval if the graph moves downward from left to right, including the points where it starts and ends this downward movement. In this case, the graph decreases from x = -2 to x = 0, and both points are part of this downward slope.
06:50:01
AI Öğretmen
Sometimes, students think the interval should be open because they believe the function only decreases between the points, but here the function value at x = -2 is higher than at x = 0, so the decrease includes these points. For example, if you look at the graph, at x = -2, f(x) = 2, and at x = 0, f(x) = 0, so the function is moving down continuously including those edges.
06:50:03
AI Öğretmen
Therefore, the correct answer should be the closed interval [-2, 0] because the function is decreasing on that entire range including the endpoints.
06:50:03
AI Öğretmen
Should we continue with the lecture?
06:51:01
Öğrenci
Alright, let's continue
06:51:02
💭 AI Öğretmen
Continuing with the lesson
06:51:13
Görsel
Görsel
06:51:14
AI Öğretmen
The maximum value of a function is the highest output it attains within a given interval.
06:51:16
AI Öğretmen
Mathematically, $f(m)$ is the maximum if, for every $x$ in the interval, $f(x) \leq f(m)$.
06:51:17
AI Öğretmen
This definition concerns the highest value on the specified interval, which is also called an absolute maximum on that interval.
06:51:18
AI Öğretmen
On a graph, this appears as the very top or "peak" point, where the function stops increasing and begins to decrease.
06:51:19
AI Öğretmen
Not all functions have a maximum in every interval, but if present, it visually resembles the top of a mountain.
06:51:19
AI Öğretmen
Did you understand how to identify the maximum value of a function on a given interval?
06:51:57
Öğrenci
I got it
06:51:59
💭 AI Öğretmen
Now, let's check understanding
06:51:59
❓ Soru basic
**Example:** The graph of $g$ is shown below. Find the intervals of $x$ for which $g(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?** ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_11a805a3-b66d-431d-99b4-450c738ea61d.png)
06:52:25
Öğrenci
My answer is: maximum value: 3
06:52:26
💭 AI Öğretmen
Noted your answer
06:52:29
AI Öğretmen
That's absolutely right! Fantastic job!
06:52:30
AI Öğretmen
You correctly identified the maximum value of the function by finding the highest point on the graph.
06:52:31
AI Öğretmen
The maximum value is the highest y-coordinate the function reaches, which in this case is 3.
06:52:33
AI Öğretmen
Keep up the great work!
06:52:33
AI Öğretmen
Therefore the correct answer is 3
06:52:34
AI Öğretmen
Should we continue with the lecture?
06:52:49
Öğrenci
Alright, let's continue
06:52:49
💭 AI Öğretmen
Moving forward now
06:53:00
Görsel
Görsel
06:53:02
AI Öğretmen
Imagine a rollercoaster moving along its track, where time is shown by \( t \) and height is shown by \( h \).
06:53:03
AI Öğretmen
Here, we have a function that shows how the height of the rollercoaster changes as time passes.
06:53:06
AI Öğretmen
This function is increasing in the interval from 0 to 5 seconds, which means as time goes from 0 to 5 seconds, the height goes up from 0 meters to 50 meters.
06:53:07
AI Öğretmen
At exactly \( t = 5 \) seconds, the rollercoaster reaches its highest point, which is 50 meters above the ground.
06:53:09
AI Öğretmen
After 5 seconds, the function starts to decrease between 5 and 10 seconds, meaning the height drops from 50 meters down to 10 meters.
06:53:10
AI Öğretmen
By saying intervals like \([0,5]\) for when the height rises and \([5,10]\) for when the height falls, we can clearly explain when the rollercoaster is going up or coming down.
06:53:11
AI Öğretmen
Did you understand how the intervals show when the height is increasing or decreasing?
06:54:15
Öğrenci
I got it
06:54:17
💭 AI Öğretmen
Let's reinforce this concept
06:54:18
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_5a453885-672f-4b3c-b466-4fe71a09d85a.png) **Example:** The graph of $f$ is shown above. Find the intervals of $x$ for which $f(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?**
06:54:52
Öğrenci
My answer is: maximum value= 2
06:54:54
💭 AI Öğretmen
Noted your answer
06:54:57
AI Öğretmen
That's absolutely right! Fantastic job!
06:54:59
AI Öğretmen
You correctly identified that the maximum value of the function is 2.
06:55:01
AI Öğretmen
This is because the maximum value is the highest y-coordinate that the function reaches on its graph.
06:55:02
AI Öğretmen
You clearly understand how to find the highest point a function reaches!
06:55:03
AI Öğretmen
Therefore the correct answer is 2.
06:55:03
AI Öğretmen
Should we continue with the lecture?
06:55:18
Öğrenci
Alright, let's continue
06:55:19
💭 AI Öğretmen
Preparing the next explanation
06:55:29
AI Öğretmen
In this lesson, we covered how to read graphs from left to right to understand a function's behavior, identified increasing and decreasing intervals, and learned how to find the maximum value of a function within a given interval. Do you have any questions about these topics? If not, we can wrap up the session.

Voltran Okul Analiz Sistemi