← Ana Rapor / Kayla Ece BAŞ / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 05:14
Bitiş
Devam ediyor
Süre
4 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Detaylı Değerlendirme

Öğrenci Performans Analizi

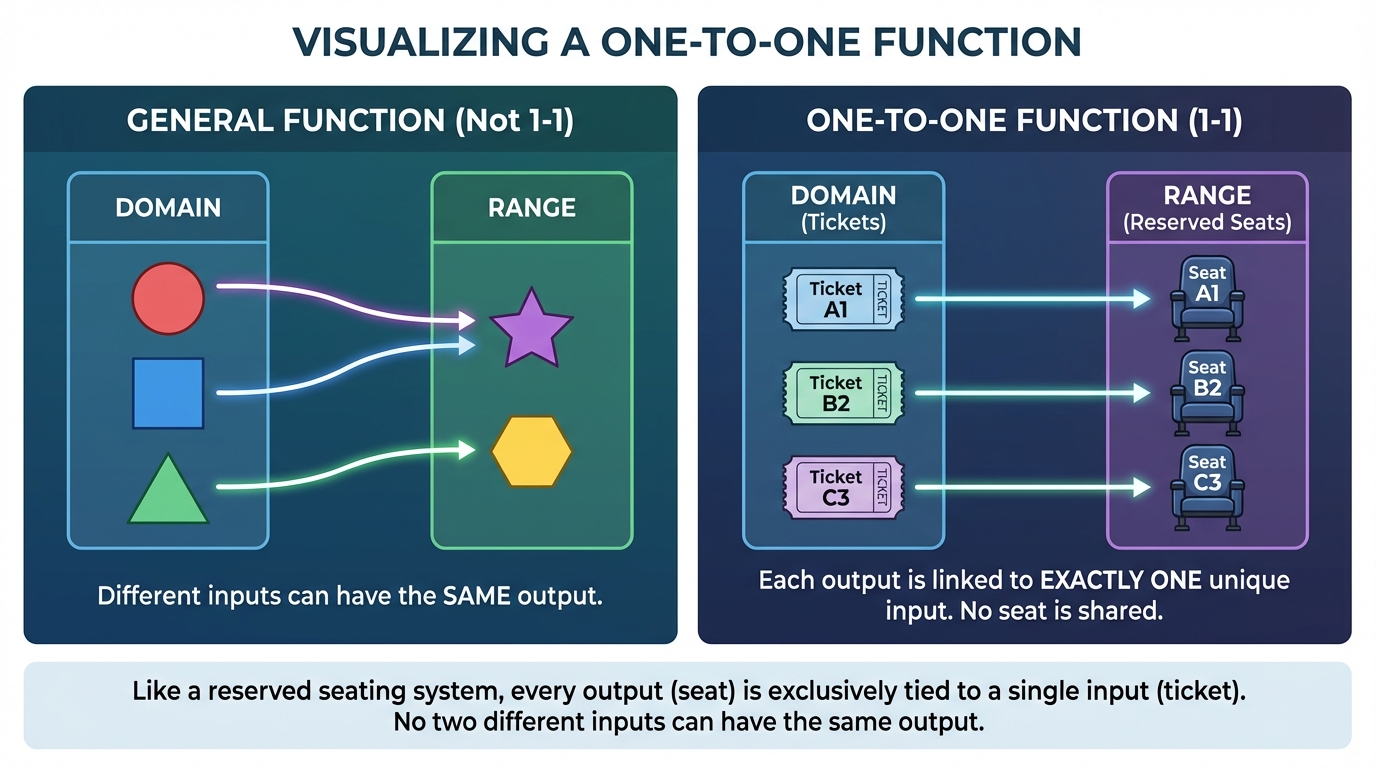
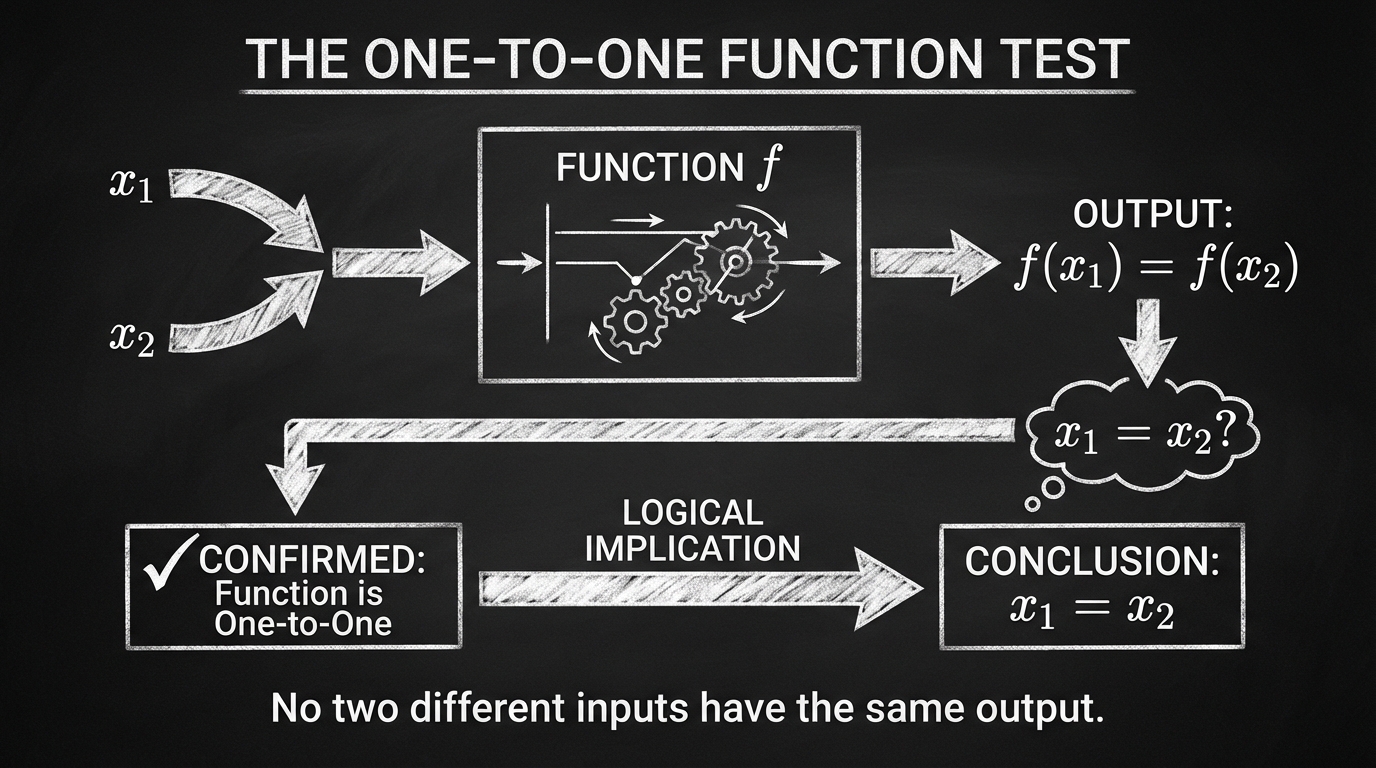
Öğrenci, "Bire Bir Fonksiyon" (One to One Function) konusuna hakimiyetini başarılı bir şekilde göstermiştir. Dersin başında konunun detaylı anlatılmasını istemiş ve ardından gelen tüm soruları doğru bir şekilde yanıtlamıştır.

# Değerlendirme Detayları:
- Kavramsal Anlama: Öğrenci, bir fonksiyonun bire bir olup olmadığını belirleme kriterini (her farklı girdinin farklı bir çıktıya sahip olması gerektiği) doğru bir şekilde anlamıştır.
- Uygulama Becerisi: Hem görsel şemalarla (eşleme diyagramları) hem de cebirsel ifadelerle (doğrusal fonksiyon) verilen fonksiyonların bire bir olup olmadığını doğru bir şekilde tespit etmiştir.
- Öğrenme Süreci: Öğrenci, açıklamaların ardından "Anladım" ("I got it") diyerek geri bildirimde bulunmuş ve sorulan soruları tereddüt etmeden, ipucu veya ek açıklamaya ihtiyaç duymadan cevaplamıştır. Herhangi bir yanlış anlama veya kafa karışıklığı belirtisi göstermemiştir.

Genel olarak, öğrencinin bu dersteki performansı oldukça başarılıdır ve konuyla ilgili herhangi bir eksikliği tespit edilmemiştir.

📜 Oturum Detayları

05:14:58
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
05:15:00
💭 AI Öğretmen
Great, preparing the details now.
05:15:00
Görsel
Görsel
05:15:03
AI Öğretmen
A one-to-one function, also called a 1-1 function, is a special kind of function.
05:15:04
AI Öğretmen
In this type of function, each output value comes from exactly one unique input.
05:15:07
AI Öğretmen
For other functions, it is possible for different inputs to create the same output, but for a one-to-one function, this is not allowed.
05:15:09
AI Öğretmen
You can think of it like a reserved seating system at a movie theater, where each ticket can only be used for one specific seat, and no two tickets are allowed to be for the same seat.
05:15:12
AI Öğretmen
With one-to-one functions, this means that every output is only linked to one input, making sure that each output is the image of at most one element from the domain.
05:15:13
AI Öğretmen
Did you understand what makes a function one-to-one?
05:15:48
Öğrenci
I got it
05:15:49
💭 AI Öğretmen
Let us reinforce this then
05:15:50
❓ Soru basic
Determine whether the following function is one-to-one: ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_185ba90c-a01e-449e-9b2f-98a502915e79.png)
05:15:59
Öğrenci
My answer is: no
05:16:00
💭 AI Öğretmen
Noted your answer
05:16:05
AI Öğretmen
Fantastic job! You're absolutely right!
05:16:06
AI Öğretmen
This function is not one-to-one because the output 'y' in set Y is mapped to by two different inputs, 'b' and 'c', from set X.
05:16:08
AI Öğretmen
A key concept for one-to-one functions is that each unique input must map to a unique output; no two different inputs can share the same output.
05:16:08
AI Öğretmen
You clearly understood that important rule!
05:16:09
AI Öğretmen
Therefore, the correct answer is no.
05:16:09
AI Öğretmen
Should we continue with the lecture?
05:16:30
Öğrenci
Alright, let's continue
05:16:31
💭 AI Öğretmen
Proceeding with lecture
05:16:38
🎥 Video
05:16:39
AI Öğretmen
Did you understand how a one-to-one function works?
05:17:05
Öğrenci
I got it
05:17:09
💭 AI Öğretmen
Let us review this topic
05:17:09
❓ Soru basic
**Example:** Determine whether the function $f: \mathbb{R} \to \mathbb{R}, f(x) = 5x - 9$ is one to one or not. Explain your reasoning.
05:17:18
Öğrenci
My answer is: yes
05:17:19
💭 AI Öğretmen
Noted your answer
05:17:21
AI Öğretmen
That's absolutely right! Great job!
05:17:22
AI Öğretmen
You correctly identified that the function $f(x) = 5x - 9$ is indeed one-to-one.
05:17:25
AI Öğretmen
This is because for every unique input, there's a unique output, and no two different inputs will ever give you the same output.
05:17:26
AI Öğretmen
Linear functions like this one, with a non-zero slope, are always one-to-one!
05:17:26
AI Öğretmen
Should we continue with the lecture?
05:17:45
Öğrenci
Alright, let's continue
05:17:46
💭 AI Öğretmen
Proceeding to next topic
05:17:52
🎥 Video
05:17:53
AI Öğretmen
Did you understand how the fingerprint example illustrates a one-to-one relationship?
05:18:20
Öğrenci
I got it
05:18:22
💭 AI Öğretmen
Let us review this carefully
05:18:22
❓ Soru basic
![image](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_8d6b21fc-51d8-4a5e-a89c-b6f20bfc4400.png) Let $A = \{1,2,3,4\}$ and $B = \{a, b, c, d\}$. Determine whether the function shown in diagram is one-to-one.
05:18:32
Öğrenci
My answer is: yes
05:18:33
💭 AI Öğretmen
Noted, processing.
05:18:37
AI Öğretmen
Fantastic job! You're absolutely right!
05:18:39
AI Öğretmen
This function is indeed one-to-one because each element in set A maps to a unique element in set B.
05:18:41
AI Öğretmen
This means no two different inputs share the same output, which is the key characteristic of a one-to-one function. Keep up the great work!
05:18:42
AI Öğretmen
Therefore, the correct answer is Yes.
05:18:42
AI Öğretmen
Should we continue with the lecture?
05:19:00
Öğrenci
Alright, let's continue
05:19:01
💭 AI Öğretmen
Preparing the next part
05:19:06
Görsel
Görsel
05:19:08
AI Öğretmen
To check if a function is one-to-one, we use logic instead of trying every possible input value.
05:19:09
AI Öğretmen
The typical approach is to assume that two outputs of the function are equal and see if this forces the inputs to also be equal.
05:19:11
AI Öğretmen
For a function $f$, the important rule is: if $f(x_1) = f(x_2)$, then this must mean $x_1 = x_2$ for the function to be one-to-one.
05:19:12
AI Öğretmen
This rule says that the function never gives the same output value to two different input values.
05:19:13
AI Öğretmen
If we can prove that whenever the outputs are equal, the inputs must be equal too, then the function is definitely one-to-one.
05:19:15
AI Öğretmen
Did you understand how to test if a function is one-to-one using the logical method?

Voltran Okul Analiz Sistemi