← Ana Rapor / Şadiye Derin ULUSOY / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:30
Bitiş
Devam ediyor
Süre
11 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci derse konuyu detaylı bir şekilde öğrenme isteğiyle başladı. Ders boyunca, öğretmenin sorduğu tüm anlama sorularına ("I got it") şeklinde olumlu yanıt verdi ve bu anladığını, sorulan tüm problem çözme sorularını doğru yanıtlayarak kanıtladı. Öğrencinin performansı, fonksiyonların temel tanımları konusunda oldukça sağlam bir anlayışa sahip olduğunu göstermektedir.

Detaylı Analiz

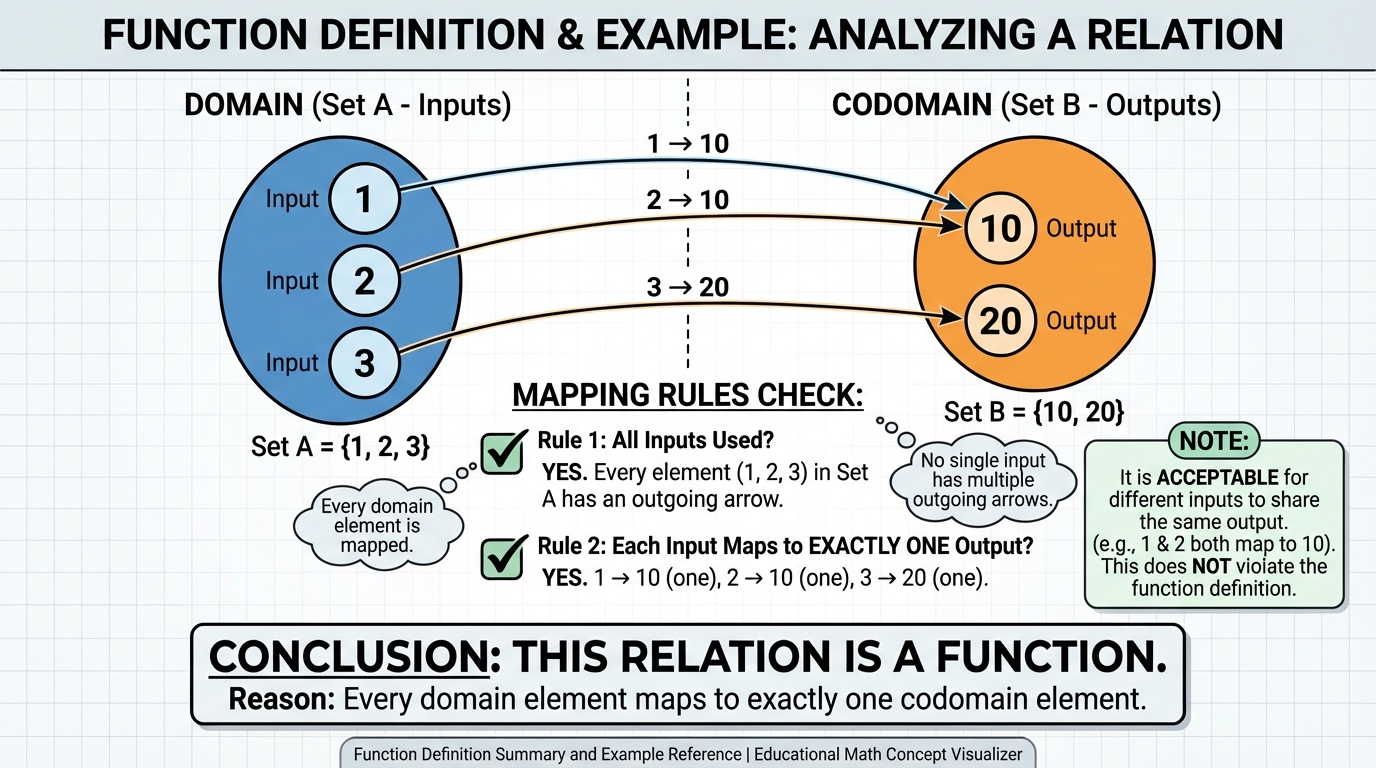
* Fonksiyon Tanımı ve Kuralları: Öğrenci, bir bağıntının hangi koşullar altında fonksiyon olarak kabul edileceğini çok iyi anlamıştır. Özellikle, tanım kümesindeki bir elemanın değer kümesinde olmayan bir sonuca eşlenemeyeceğini (doğal sayılar sorusu) ve rasyonel bir fonksiyonda paydayı sıfır yapan değerin tanım kümesinde olamayacağını (en geniş tanım kümesi sorusu) doğru bir şekilde tespit etmiştir.
* Tanım, Değer ve Görüntü Kümesi: Tanım (domain), değer (codomain) ve görüntü (range) kümelerini ayırt etme ve verilen bir fonksiyona göre bu kümeleri doğru bir şekilde belirleme konusunda hiçbir hata yapmamıştır.
* Fonksiyonel Değer Bulma: `f(x-1)` formatında verilen bir fonksiyonda `f(3)` değerini bulma gibi daha karmaşık bir soruyu bile doğru adımları izleyerek (önce doğru `x` değerini bularak, sonra yerine koyarak) hatasız bir şekilde çözmüştür.

Sonuç

Öğrenci, "Formal Definitions of Functions" alt konusuyla ilgili tüm temel kavramları ve uygulamaları başarıyla kavramıştır. Ders boyunca herhangi bir bilgi eksikliği veya kafa karışıklığı gözlemlenmemiştir. Bu konuyla ilgili temel bilgi seviyesi mükemmeldir.

📜 Oturum Detayları

06:30:38
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:30:39
💭 AI Öğretmen
Great, preparing the explanation now
06:30:39
🎥 Video
06:30:40
AI Öğretmen
Did you understand how a function relates elements from Set A to Set B?
06:31:18
Öğrenci
I got it
06:31:20
💭 AI Öğretmen
Let us continue now
06:31:20
🎥 Video
06:31:20
AI Öğretmen
Did you understand how the domain, codomain, and range relate to each other in a function?
06:31:58
Öğrenci
I got it
06:32:00
💭 AI Öğretmen
Let us proceed with a question
06:32:01
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:32:50
Öğrenci
My answer is: Domain: -1,0,1,2 Codomain: 0,1,2,3,4,5, Range: 0,1,4
06:32:51
💭 AI Öğretmen
Let me review that answer
06:32:55
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range of the function.
06:32:57
AI Öğretmen
You clearly understand that the domain is all the input values, the codomain is all possible output values, and the range is the set of actual output values that are mapped to.
06:32:58
AI Öğretmen
This shows a great grasp of function fundamentals! Keep up the excellent work!
06:32:59
AI Öğretmen
Therefore, the correct answer is Domain: $\{-1, 0, 1, 2\}$, Codomain: $\{0, 1, 2, 3, 4, 5\}$, Range: $\{0, 1, 4\}$.
06:33:00
AI Öğretmen
Should we continue with the lecture?
06:33:32
Öğrenci
Alright, let's continue
06:33:33
💭 AI Öğretmen
Moving forward now
06:33:48
Görsel
Görsel
06:33:50
AI Öğretmen
A relation is considered a function if every input from the domain, also called Set A, is matched to an output in the codomain, or Set B.
06:33:51
AI Öğretmen
This means that each element from Set A has exactly one partner in Set B, so no input is left without an output.
06:33:53
AI Öğretmen
It is important to know that not every element in the codomain, or Set B, needs to have a match; there can be elements in Set B that are not outputs of any input.
06:33:54
AI Öğretmen
It is also allowed for different inputs from the domain to share the same output in the codomain, so many-to-one mappings are fine.
06:33:56
AI Öğretmen
However, a single input from the domain cannot be connected to more than one output; one-to-many associations are not allowed.
06:33:57
AI Öğretmen
In summary, a function assigns exactly one value from the codomain to each element of the domain.
06:33:58
AI Öğretmen
Did you understand how a relation qualifies as a function based on the input-output rule?
06:34:49
Öğrenci
I got it
06:34:52
💭 AI Öğretmen
Now let's review this
06:34:52
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:37:00
Öğrenci
My answer is: This relation maps natural numbers to natural numbers. when f(2) = 2-3 =-1 So this is not a natural number which means that the relation is not a function.
06:37:02
💭 AI Öğretmen
Let me review that answer
06:37:06
AI Öğretmen
That's absolutely right! Fantastic job explaining why this relation isn't a function.
06:37:08
AI Öğretmen
You correctly pointed out that for values like $x=2$, the output $f(2) = -1$ is not a natural number, even though 2 is.
06:37:09
AI Öğretmen
This shows a great understanding that for a relation to be a function, every element in its domain must map to an element *within* its specified codomain.
06:37:10
AI Öğretmen
Keep up the excellent work!
06:37:11
AI Öğretmen
Therefore, the correct answer is No, it is not a function.
06:37:11
AI Öğretmen
Should we continue with the lecture?
06:37:37
Öğrenci
Alright, let's continue
06:37:38
💭 AI Öğretmen
Moving forward now
06:37:43
Görsel
Görsel
06:37:45
AI Öğretmen
A relation between two sets can be checked to see if it's a function by following certain rules.
06:37:47
AI Öğretmen
Let's look at two sets: Set A, which has the inputs $\{1, 2, 3\}$, and Set B, the outputs $\{10, 20\}$.
06:37:49
AI Öğretmen
The mapping here is: $1$ maps to $10$, $2$ maps to $10$, and $3$ maps to $20$.
06:37:50
AI Öğretmen
Each element from Set A, which are 1, 2, and 3, is assigned to exactly one element in Set B.
06:37:53
AI Öğretmen
It's okay that different elements from Set A (like 1 and 2) both map to $10$ in Set B.
06:37:54
AI Öğretmen
The important thing is that every input from Set A is matched with only one output in Set B.
06:37:55
AI Öğretmen
So, this relation is a function, because every element in the domain has exactly one image in the codomain.
06:37:56
AI Öğretmen
Did you understand why this relation is considered a function?
06:38:31
Öğrenci
I got it
06:38:34
💭 AI Öğretmen
Let us review this question
06:38:34
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:39:06
Öğrenci
My answer is: Domf= R-(-2)
06:39:06
💭 AI Öğretmen
Let me review that
06:39:12
AI Öğretmen
Fantastic job!
06:39:14
AI Öğretmen
You've correctly identified that for a rational function, the denominator cannot be zero.
06:39:15
AI Öğretmen
This is a super important concept because division by zero is undefined, and you nailed it by excluding the value that makes the denominator zero.
06:39:16
AI Öğretmen
Keep up the great work!
06:39:17
AI Öğretmen
Therefore, the correct answer is Domf= R-(-2).
06:39:17
AI Öğretmen
Should we continue with the lecture?
06:39:37
Öğrenci
Alright, let's continue
06:39:38
💭 AI Öğretmen
Preparing the next part
06:39:46
AI Öğretmen
A relation is considered a function if each element from the domain is paired with only one element in the codomain.
06:39:47
AI Öğretmen
This means that for every input value, there is only a single output value assigned to it.
06:39:48
AI Öğretmen
It is important to note that different inputs are allowed to have the same output in a function.
06:39:50
AI Öğretmen
Shared outputs do not break the rule of being a function, as long as no single input has more than one output.
06:39:51
AI Öğretmen
Does this explanation make sense to you, or would you like me to go over any part again?
06:40:17
Öğrenci
I got it
06:40:19
💭 AI Öğretmen
Now, let's check understanding
06:40:19
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:40:57
Öğrenci
My answer is: x= 4 so 4x4+2= 16+2=18
06:40:58
💭 AI Öğretmen
Noted your answer
06:41:03
AI Öğretmen
That's absolutely spot on! Fantastic job!
06:41:04
AI Öğretmen
You correctly figured out that to find $f(3)$, you needed to set $x-1$ equal to 3, which gave you $x=4$.
06:41:05
AI Öğretmen
Then, you skillfully substituted that value of $x$ into the expression $4x+2$ to get the correct result.
06:41:07
AI Öğretmen
This shows a great understanding of how to work with function notation and substitution. Keep up the excellent work!
06:41:08
AI Öğretmen
Therefore, the correct answer is 18.
06:41:08
AI Öğretmen
Should we continue with the lecture?
06:41:33
Öğrenci
Alright, let's continue
06:41:34
💭 AI Öğretmen
Moving forward now
06:41:50
AI Öğretmen
In this lesson, we covered the definition of a function as a relation where each input from the domain maps to exactly one output in the codomain. We also discussed the concepts of domain, codomain, and range, and how to determine if a relation is a function by checking these mappings. Additionally, we looked at examples to identify domain, codomain, and range, and how to evaluate functions for specific inputs. Do you have any questions about these topics? If not, I'll end the lesson.

Voltran Okul Analiz Sistemi