← Ana Rapor / Kübra CAN / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:44
Bitiş
Devam ediyor
Süre
15 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
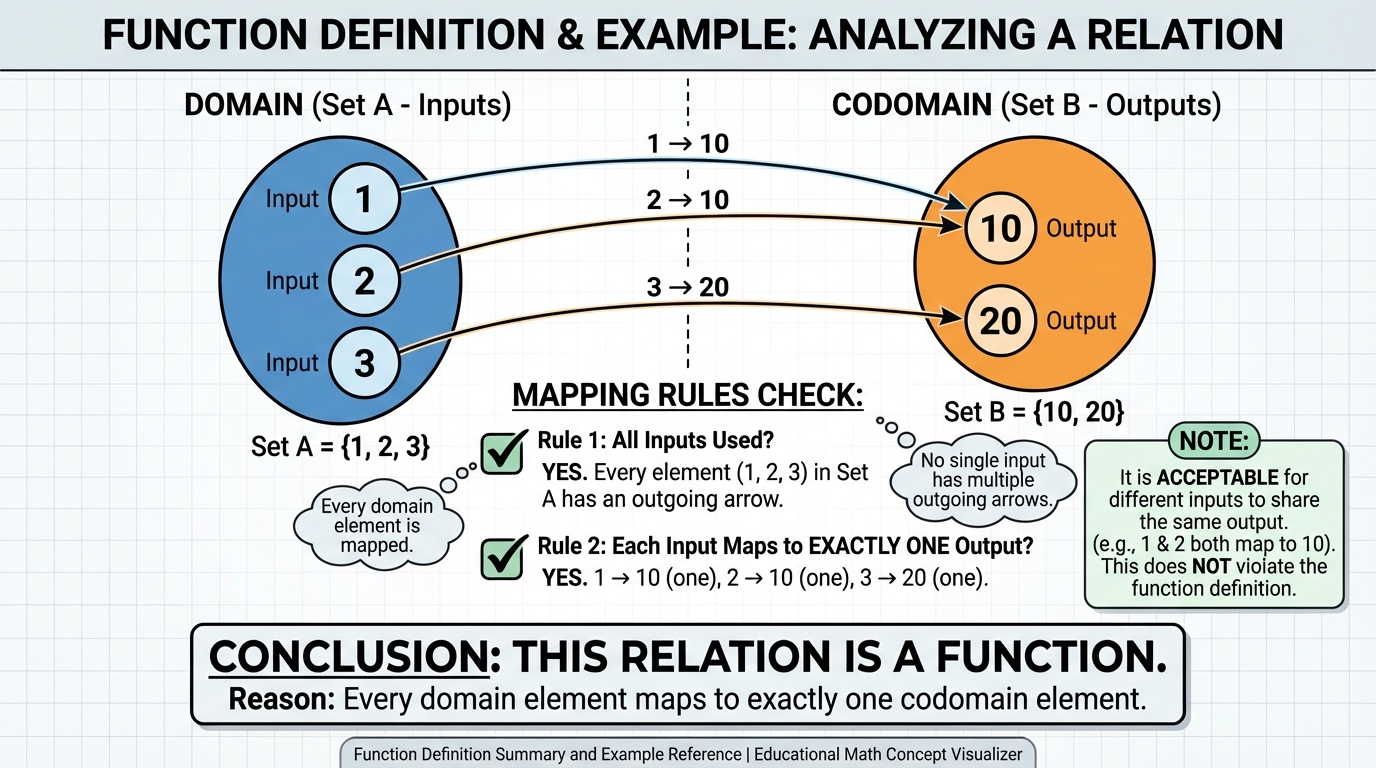
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Genel Değerlendirme
Öğrenci derse konunun detaylı bir şekilde anlatılmasını isteyerek başladı. Bu, konuya başlangıçta hakim olmadığını veya özgüven eksikliği olduğunu gösterebilir. Dersin başında, bir fonksiyonun tanım kümesi (domain), değer kümesi (codomain) ve görüntü kümesini (range) tanımlama gibi temel kavramları doğru bir şekilde anladığını gösterdi. Ayrıca, bir bağıntının hangi koşulda fonksiyon olup olmadığını (doğal sayılar örneğinde olduğu gibi) doğru bir şekilde gerekçelendirerek açıkladı.

Ancak, ders ilerledikçe daha karmaşık ve uygulamaya yönelik sorularda ciddi zorluklar yaşadı. Özellikle iki temel alanda önemli eksiklikler gözlemlendi:
1. Rasyonel Fonksiyonların Tanım Kümesini Bulma: Paydayı sıfır yapan değeri bularak tanım kümesini belirlemesi gereken soruda, öğrenci tamamen ilgisiz bir cevap verdi. Bu, rasyonel fonksiyonların temel özelliklerini ve tanım kümesi kısıtlamalarını anlamadığını gösteriyor.
2. Fonksiyon Değerini Hesaplama: `f(x-1)` gibi bir ifade verildiğinde `f(3)` değerini bulması gereken soruda, doğru `x` değerini nasıl bulacağını ve yerine koyacağını anlayamadı. Bu, fonksiyon notasyonunun işleyişi ve değer bulma konusunda temel bir yanılgıya sahip olduğunu ortaya koydu.

Öğrencinin Performansı
- Başlangıç: Konunun temellerini (domain, range, fonksiyon olma şartı) anladı ve ilk soruları doğru yanıtladı.
- İlerleme: Konunun daha teknik ve cebirsel uygulamalarına geçildiğinde performansı belirgin şekilde düştü. İki kritik soruyu yanlış yanıtladı ve bu soruların çözümleri için detaylı açıklamalara ihtiyaç duydu.

Sonuç
Öğrencinin fonksiyonların temel mantıksal tanımını kavradığı ancak cebirsel uygulamalarında ve özel fonksiyon türlerinin (rasyonel fonksiyonlar gibi) analizinde önemli eksiklikleri olduğu tespit edilmiştir. Bu konuların üzerine tekrar gidilmesi ve bol pratik yapılması gerekmektedir.

📜 Oturum Detayları

06:44:23
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:44:24
💭 AI Öğretmen
Getting the details ready
06:44:24
🎥 Video
06:44:25
AI Öğretmen
Did you understand how a function relates elements from Set A to Set B?
06:45:15
Öğrenci
I got it
06:45:17
💭 AI Öğretmen
Let us continue then
06:45:17
🎥 Video
06:45:18
AI Öğretmen
Do you feel clear about the differences between domain, codomain, and range?
06:45:54
Öğrenci
I got it
06:45:57
💭 AI Öğretmen
Let us move forward
06:45:57
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:48:36
Öğrenci
My answer is: Domain: ｛-1, 0, 1 2｝ Codomain ﹛0,1,2,3,4,5,｝ Range ｛0,1,4｝
06:48:37
💭 AI Öğretmen
That is noted.
06:48:41
AI Öğretmen
Fantastic job! You've absolutely nailed it!
06:48:42
AI Öğretmen
You correctly identified the domain as all the input values in set A, the codomain as all possible output values in set B, and the range as the specific values in B that are actually mapped to by the function.
06:48:44
AI Öğretmen
Understanding these concepts is super important for working with functions, and you've shown a great grasp of them!
06:48:47
AI Öğretmen
Your answer: Domain: $\{-1, 0, 1, 2\}$, Codomain: $\{0, 1, 2, 3, 4, 5\}$, Range: $\{0, 1, 4\}$ is perfectly correct!
06:48:47
AI Öğretmen
Should we continue with the lecture?
06:49:14
Öğrenci
Alright, let's continue
06:49:15
💭 AI Öğretmen
Moving to next part
06:49:21
Görsel
Görsel
06:49:23
AI Öğretmen
A relation is considered a function if it follows an important rule.
06:49:26
AI Öğretmen
Every input from the domain, which we can call Set A, must be linked to some output in the codomain, or Set B.
06:49:28
AI Öğretmen
This means each element from Set A is connected to one value in Set B.
06:49:29
AI Öğretmen
Not every element in Set B has to be used, so there can be outputs in the codomain that are not connected to any input from the domain.
06:49:30
AI Öğretmen
It's also allowed for different inputs to produce the same output, so multiple values from Set A can have matching results in Set B.
06:49:33
AI Öğretmen
However, one input from Set A cannot be paired with more than one output in Set B, which means one-to-many mappings are not allowed.
06:49:33
AI Öğretmen
So, a function always assigns exactly one output to each input, ensuring that every element in the domain has only one corresponding value in the codomain.
06:49:34
AI Öğretmen
Did you understand how a function relates elements from the domain to the codomain?
06:50:17
Öğrenci
I got it
06:50:19
💭 AI Öğretmen
Let us proceed with the question
06:50:19
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:51:26
Öğrenci
My answer is: its not a function because when we put a number less then 3 to the x its not a naturel number
06:51:27
💭 AI Öğretmen
Let me review that reasoning
06:51:33
AI Öğretmen
That's absolutely right! Fantastic job explaining why this is not a function.
06:51:34
AI Öğretmen
You correctly pointed out that if you input a natural number less than 3, like 1 or 2, the result would be a negative number, which isn't in the set of natural numbers.
06:51:37
AI Öğretmen
This shows you understand that for a relation to be a function, every element in the domain must map to an element *within* the specified codomain. Keep up the great thinking!
06:51:38
AI Öğretmen
Therefore, the correct answer is No, it is not a function.
06:51:38
AI Öğretmen
Should we continue with the lecture?
06:52:05
Öğrenci
Alright, let's continue
06:52:06
💭 AI Öğretmen
Preparing the next explanation
06:52:12
Görsel
Görsel
06:52:14
AI Öğretmen
A relation between two sets can be analyzed to determine if it is a function by checking specific rules.
06:52:16
AI Öğretmen
Consider two sets: Set A represents the inputs and is given as $\{1, 2, 3\}$, while Set B represents the outputs and is given as $\{10, 20\}$.
06:52:17
AI Öğretmen
The mappings in this relation are: $1$ maps to $10$, $2$ maps to $10$, and $3$ maps to $20$.
06:52:19
AI Öğretmen
Each element in Set A, which are $1$, $2$, and $3$, is used in the mapping, with the pairs being $1 \to 10$, $2 \to 10$, and $3 \to 20$.
06:52:20
AI Öğretmen
This means all inputs from Set A are used, and importantly, each input is matched to only one output in Set B.
06:52:21
AI Öğretmen
It is allowed for different inputs to have the same output, like $1$ and $2$ both mapping to $10$.
06:52:22
AI Öğretmen
As a result, this relation is a function because every input from the domain is paired with exactly one output from the codomain.
06:52:23
AI Öğretmen
Did you understand why this relation is considered a function?
06:53:17
Öğrenci
I got it
06:53:19
💭 AI Öğretmen
Let us review this carefully.
06:53:20
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:53:50
Öğrenci
My answer is: x-2
06:53:51
💭 AI Öğretmen
Let me review that answer
06:53:56
AI Öğretmen
Your answer was not correct, let me explain why. The question asks for the largest domain of the function \( f(x) = \frac{4}{x+2} \), which means we need to find all values of \( x \) for which the function is defined.
06:53:58
AI Öğretmen
The key point is that the function is undefined when the denominator is zero, because division by zero is not allowed. So, we set the denominator \( x + 2 \neq 0 \), which means \( x \neq -2 \).
06:54:00
AI Öğretmen
Therefore, the function is defined for all real numbers except \( x = -2 \). This is why the largest domain is all real numbers except \(-2\), written as \( \{x \in \mathbb{R} \mid x \neq -2\} \).
06:54:02
AI Öğretmen
A common misconception might be mixing up the expression \( x-2 \) with the domain restriction. Remember, the domain is about where the function is defined, not just rewriting the denominator.
06:54:04
AI Öğretmen
For example, if the function was \( \frac{1}{x-3} \), the domain would exclude \( x = 3 \) because the denominator becomes zero there.
06:54:07
AI Öğretmen
Therefore, the correct answer should be \( \{x \in \mathbb{R} \mid x \neq -2\} \).
06:54:07
AI Öğretmen
Should we continue with the lecture?
06:55:08
Öğrenci
Alright, let's continue
06:55:09
💭 AI Öğretmen
Preparing the next part
06:55:15
AI Öğretmen
A relation is considered a function when every input in its domain is paired with one and only one output in the codomain.
06:55:16
AI Öğretmen
This means you can't have a single input linked to two or more different outputs in a function.
06:55:18
AI Öğretmen
It's perfectly fine if two or more different inputs share the same output, but each input still must connect to just one output.
06:55:19
AI Öğretmen
In summary, as long as every input gives a single output, the relation is a function, even if some outputs are repeated for different inputs.
06:55:19
AI Öğretmen
Does this explanation about when a relation qualifies as a function make sense to you?
06:55:54
Öğrenci
I got it
06:55:56
💭 AI Öğretmen
Let us review this next question
06:55:56
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:57:28
Öğrenci
My answer is: 4
06:57:29
💭 AI Öğretmen
Let me review that answer
06:57:34
AI Öğretmen
Your answer was not correct, let me explain why.
06:57:36
AI Öğretmen
The function is given as \( f(x - 1) = 4x + 2 \), and we want to find \( f(3) \). To do this, notice that inside the function, the input is \( x - 1 \), so we set \( x - 1 = 3 \).
06:57:37
AI Öğretmen
Solving for \( x \), we get \( x = 4 \). Now, substitute \( x = 4 \) into the right side of the equation: \( 4x + 2 = 4(4) + 2 = 16 + 2 = 18 \).
06:57:40
AI Öğretmen
Therefore, \( f(3) = 18 \). A common mistake is to confuse the input \( 3 \) directly with \( x \), but here the input is \( x - 1 \), so we must find the corresponding \( x \) first.
06:57:43
AI Öğretmen
For example, if the function was \( f(x-1) = 2x + 3 \) and you want \( f(2) \), set \( x - 1 = 2 \) which means \( x = 3 \), then \( f(2) = 2(3) + 3 = 9 \).
06:57:44
AI Öğretmen
Therefore, the correct answer should be 18.
06:57:44
AI Öğretmen
Should we continue with the lecture?
06:59:02
Öğrenci
Alright, let's continue
06:59:04
💭 AI Öğretmen
Continuing shortly
06:59:13
AI Öğretmen
In this lesson, we explored the concept of functions as special relations between two sets where each input in the domain maps to exactly one output in the codomain. We discussed the roles of domain, codomain, and range, and clarified that while multiple inputs can share the same output, one input cannot have multiple outputs. We also looked at examples to determine whether a relation is a function based on these rules. Do you have any questions about these topics? If not, we can wrap up the session.

Voltran Okul Analiz Sistemi