← Ana Rapor / Ela ENGÜR / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:29
Bitiş
Devam ediyor
Süre
15 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, dersin başında konunun detaylı bir şekilde anlatılmasını isteyerek öğrenmeye istekli olduğunu göstermiştir. Ders boyunca, yapay zeka öğretmenin açıklamalarından sonra "Anladım" ("I got it") diyerek ilerlemiş ve sorulan tüm sorulara istisnasız doğru cevaplar vermiştir. Bu durum, öğrencinin konuyu temel düzeyde anladığını göstermektedir.

Performans Detayları

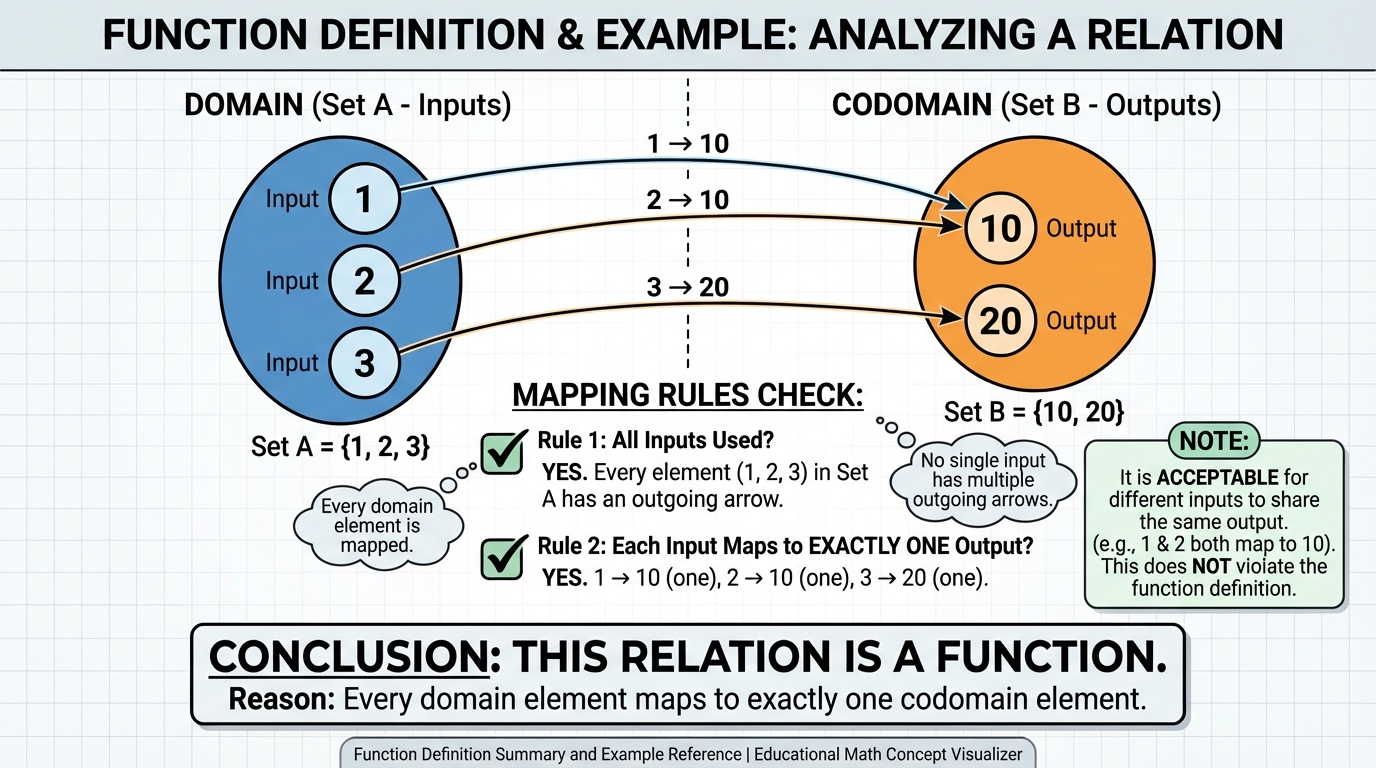
- Tanım Kümesi, Değer Kümesi ve Görüntü Kümesi: Fonksiyonun tanım, değer ve görüntü kümelerini doğru bir şekilde tespit etmiştir.
- Fonksiyon Olma Şartı: Bir bağıntının hangi durumlarda fonksiyon olup olmayacağını doğru bir şekilde analiz edebilmiştir. Özellikle, doğal sayılar kümesinde tanımlı bir bağıntının neden bir fonksiyon olmadığını doğru bir şekilde açıklamıştır.
- Tanım Kümesi Bulma: Verilen rasyonel bir ifadenin en geniş tanım kümesini, paydayı sıfır yapan değeri bularak doğru bir şekilde belirlemiştir.
- Fonksiyonda Değer Bulma: `f(x-1)` formatında verilen bir fonksiyonda `f(3)` değerini bulmak için doğru adımları izlemiş ve doğru sonuca ulaşmıştır.

Sonuç olarak, öğrencinin "Fonksiyonların Tanımı" konusunda herhangi bir eksikliği gözlemlenmemiştir. Sorulan tüm soruları başarıyla yanıtlamış ve konuya hakim olduğunu kanıtlamıştır.

📜 Oturum Detayları

06:29:29
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:29:30
💭 AI Öğretmen
Preparing detailed explanation
06:29:30
🎥 Video
06:29:31
AI Öğretmen
Did you understand how a function relates elements from Set A to Set B?
06:30:40
Öğrenci
I got it
06:30:42
💭 AI Öğretmen
Great, moving forward
06:30:42
🎥 Video
06:30:43
AI Öğretmen
Did you understand how the domain, codomain, and range relate to each other in a function?
06:31:21
Öğrenci
I got it
06:31:24
💭 AI Öğretmen
Good, let's proceed
06:31:24
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:32:27
Öğrenci
My answer is: Domain: -1, 0, 1, 2 Codomain: 0, 1, 2, 3, 4, 5 Range: 0, 1, 4
06:32:28
💭 AI Öğretmen
Let me review that answer
06:32:35
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range of the function.
06:32:37
AI Öğretmen
You clearly understand that the domain is all the input values in set A, and the codomain is all the possible output values in set B.
06:32:39
AI Öğretmen
It's great that you also accurately picked out the range, which includes only the elements in set B that are actually mapped to by an element in set A.
06:32:40
AI Öğretmen
Keep up the excellent work distinguishing between these important function concepts!
06:32:42
AI Öğretmen
Therefore, the correct answer is Domain: $\{-1, 0, 1, 2\}$, Codomain: $\{0, 1, 2, 3, 4, 5\}$, Range: $\{0, 1, 4\}$.
06:32:42
AI Öğretmen
Should we continue with the lecture?
06:33:20
Öğrenci
Alright, let's continue
06:33:20
💭 AI Öğretmen
Proceeding to next part
06:33:26
Görsel
Görsel
06:33:28
AI Öğretmen
A relation is called a function if it follows this important rule.
06:33:30
AI Öğretmen
Every input from the Domain, or Set A, must be matched to one output in the Codomain, or Set B.
06:33:32
AI Öğretmen
This means that for each value you start with (the input), the function tells you exactly where to go (the output).
06:33:34
AI Öğretmen
It is okay if some elements in the Codomain, or Set B, are not used as outputs.
06:33:35
AI Öğretmen
This means that not every item in the Codomain must be linked to something from the Domain; there can be leftovers.
06:33:36
AI Öğretmen
Different inputs from the Domain can share the same output in the Codomain, so two or more starting points can connect to the same ending point.
06:33:37
AI Öğretmen
However, one input cannot be assigned to more than one output. This is not allowed.
06:33:38
AI Öğretmen
A function always assigns exactly one value in the Codomain to each value from the Domain.
06:33:38
AI Öğretmen
Did you understand how a function relates elements from the domain to the codomain?
06:34:31
Öğrenci
I got it
06:34:33
💭 AI Öğretmen
Let us reinforce this concept
06:34:33
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:35:01
Öğrenci
My answer is: Not function
06:35:02
💭 AI Öğretmen
Let me review that answer
06:35:06
AI Öğretmen
That's absolutely right! Fantastic job!
06:35:08
AI Öğretmen
You correctly identified that this relation is not a function because for some natural numbers in the domain, like 1 or 2, the output $f(x) = x - 3$ would not be a natural number.
06:35:08
AI Öğretmen
This shows you understand that for a relation to be a function, every input from the domain must have a corresponding output that exists within the specified codomain. Keep up the great work!
06:35:09
AI Öğretmen
Therefore, the correct answer is: Not a function.
06:35:09
AI Öğretmen
Should we continue with the lecture?
06:35:39
Öğrenci
Alright, let's continue
06:35:39
💭 AI Öğretmen
Continuing shortly
06:35:45
Görsel
Görsel
06:35:47
AI Öğretmen
A relation between two sets can be analyzed to determine if it is a function by checking specific rules.
06:35:48
AI Öğretmen
Consider two sets: Set A called Inputs, which has the elements $\{1, 2, 3\}$, and Set B called Outputs, which has the elements $\{10, 20\}$.
06:35:51
AI Öğretmen
The given mappings are $1 \to 10$, $2 \to 10$, and $3 \to 20$.
06:35:53
AI Öğretmen
Each element in Set A, which are 1, 2, and 3, is mapped to an element in Set B.
06:35:54
AI Öğretmen
All the input elements (1, 2, and 3) have a mapping, and each input is paired with only one output.
06:35:56
AI Öğretmen
It is acceptable for different inputs to have the same output; for example, both 1 and 2 are connected to 10.
06:35:58
AI Öğretmen
The conclusion is that this relation is a function because every input from the domain is mapped to exactly one output in the codomain.
06:35:59
AI Öğretmen
Did you understand why this relation qualifies as a function?
06:36:40
Öğrenci
I got it
06:36:42
💭 AI Öğretmen
Let us review this carefully
06:36:43
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:37:58
Öğrenci
My answer is: Domf=R-(-2)
06:37:59
💭 AI Öğretmen
Let me review that answer
06:38:02
AI Öğretmen
That's absolutely spot on! Fantastic job!
06:38:03
AI Öğretmen
You correctly identified that the denominator of a fraction cannot be zero, which is the key restriction for rational functions like this one.
06:38:05
AI Öğretmen
By setting $x+2 \neq 0$, you found the exact value that needs to be excluded from the domain. Keep up the great work!
06:38:07
AI Öğretmen
Therefore, the correct answer is Domf=R-(-2).
06:38:07
AI Öğretmen
Should we continue with the lecture?
06:39:39
Öğrenci
Alright, let's continue
06:39:40
💭 AI Öğretmen
Proceeding to next section
06:39:50
AI Öğretmen
A relation is called a function when each input from the domain is paired with exactly one output in the codomain.
06:39:51
AI Öğretmen
This means that for every value you start with, there is only one answer or result you can get.
06:39:52
AI Öğretmen
It is still allowed for different inputs to have the same output, so outputs can be shared.
06:39:53
AI Öğretmen
What matters is that a single input cannot point to more than one output for the relation to be a function.
06:39:54
AI Öğretmen
Does this explanation about functions make sense to you?
06:42:22
Öğrenci
I got it
06:42:24
💭 AI Öğretmen
Now let's review this question
06:42:25
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:43:09
Öğrenci
My answer is: x-1 = 3 x = 4 4 x 4 + 2 = 18
06:43:10
💭 AI Öğretmen
Let me review that
06:43:14
AI Öğretmen
Fantastic job! You've absolutely nailed it!
06:43:15
AI Öğretmen
You correctly understood that to find $f(3)$, you need to set the expression inside the parentheses, $x-1$, equal to 3.
06:43:16
AI Öğretmen
This allowed you to find the correct value for $x$ and then substitute it back into the function's rule to get the right answer. Great thinking!
06:43:18
AI Öğretmen
Therefore, the correct answer is 18.
06:43:18
AI Öğretmen
Should we continue with the lecture?
06:44:13
Öğrenci
Alright, let's continue
06:44:14
💭 AI Öğretmen
Moving forward now
06:44:23
AI Öğretmen
In this lesson, we covered the definition of a function as a relation where each input from the domain maps to exactly one output in the codomain. We also discussed the roles of domain, codomain, and range, and how to determine if a relation is a function by checking that each input has a unique output. We looked at examples illustrating these concepts. Do you have any questions about what we covered? If not, I’ll end the lesson here.

Voltran Okul Analiz Sistemi