← Ana Rapor / Zeynep Aylin USTA / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:27
Bitiş
02 December 2025, 06:43
Süre
15 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
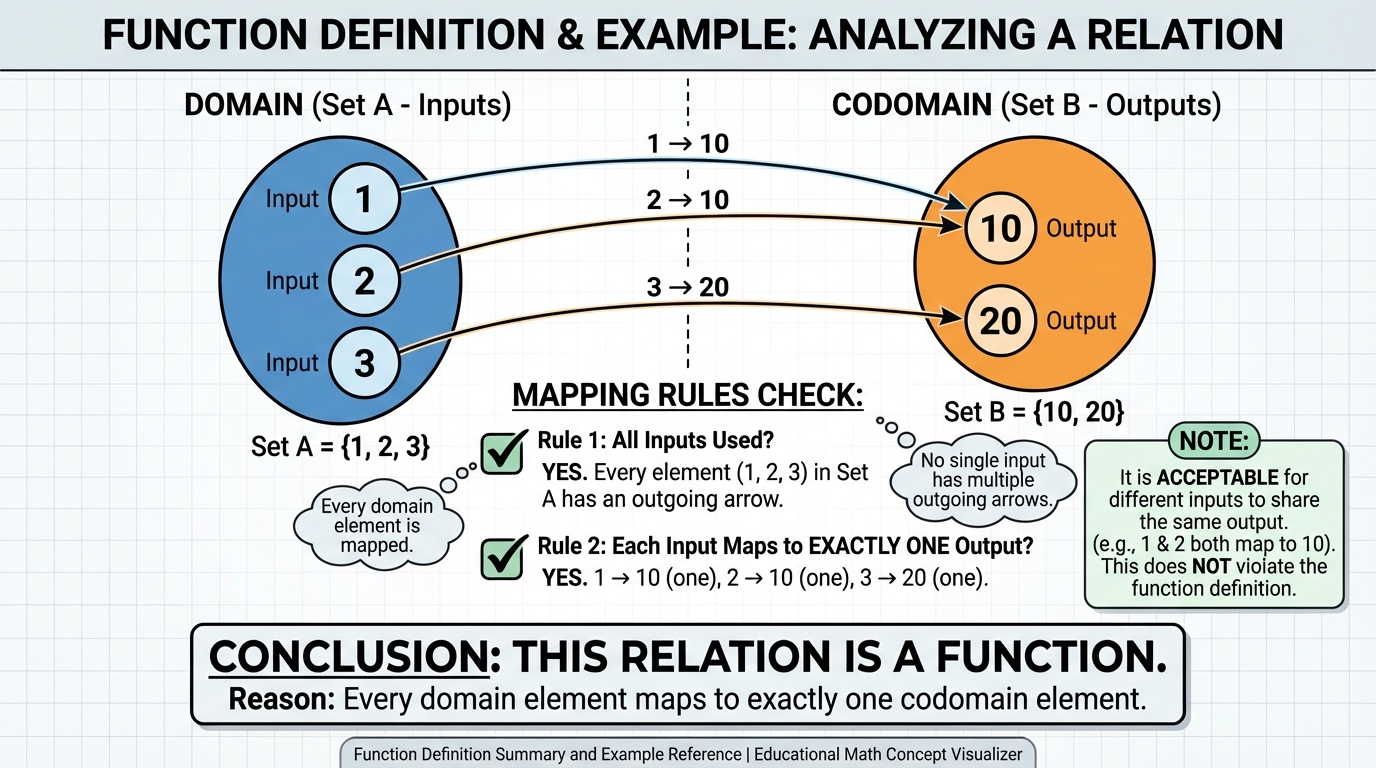
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci ders boyunca konuya ilgili ve katılımcı bir tutum sergiledi. Dersin başında ve ortasında sorduğu "How can we represent the range of a function mathematically?" gibi sorular, konuyu daha derinlemesine anlama isteğini gösteriyor. Öğrenci, bir ifadenin fonksiyon olup olmadığını belirleme, şemadan tanım, değer ve görüntü kümesini bulma ve fonksiyonun değerini hesaplama gibi konularda başarılı oldu.

Ancak, bir fonksiyonun en geniş tanım kümesini bulma konusunda ciddi bir eksiklik gözlemlendi. Rasyonel bir fonksiyonun tanım kümesi sorulduğunda (06:38:17), paydanın sıfır olmaması gerektiği kuralını uygulayamadı ve cevabı matematiksel olarak doğru bir şekilde ifade edemedi. Bu konu, fonksiyonların temelini oluşturduğu için üzerinde tekrar durulması gereken kritik bir noktadır.

Öğrencinin İyi Olduğu Konular

Öğrenci, aşağıdaki konularda başarılı bir performans göstermiştir:
- Bir eşlemenin fonksiyon olup olmadığına karar verme.
- Şema ile verilen bir fonksiyonun tanım, değer ve görüntü kümelerini doğru bir şekilde belirleme.
- Fonksiyonda değer bulma (karmaşık bir fonksiyon değerlendirme sorusunu doğru cevapladı).

Geliştirilmesi Gereken Konular

Öğrencinin aşağıdaki konularda eksiklikleri bulunmaktadır ve tekrar etmesi önerilir:
- Özellikle rasyonel ifadelerde bir fonksiyonun en geniş tanım kümesini bulma. Öğrenci, fonksiyonu tanımsız yapan değeri sezgisel olarak anlasa da bunu matematiksel bir küme olarak ifade etmekte zorlanmıştır.

Ders Dışı Sorular/Yorumlar

Ders sırasında konu dışı herhangi bir soru veya yorum kaydedilmemiştir.

📜 Oturum Detayları

06:28:08
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:28:09
💭 AI Öğretmen
Certainly, just a moment.
06:28:09
🎥 Video
06:28:11
AI Öğretmen
Did you understand how a function assigns exactly one output to each input?
06:28:49
Öğrenci
I got it
06:28:51
💭 AI Öğretmen
Let us continue now
06:28:52
🎥 Video
06:28:53
AI Öğretmen
Do you feel clear about the difference between domain, codomain, and range?
06:29:35
Öğrenci
How can we represent the range of a function mathematically?
06:29:38
💭 AI Öğretmen
Let me review this
06:29:42
AI Öğretmen
The range of a function can be represented mathematically as the set of all outputs the function actually produces. If the function is \( f: A \to B \), then the range is written as \( \{ f(x) \mid x \in A \} \), meaning all values \( f(x) \) for inputs \( x \) in the domain \( A \).
06:29:43
AI Öğretmen
This set is a subset of the codomain \( B \) and shows exactly which values are hit by the function.
06:29:45
AI Öğretmen
Does this explanation make sense to you? Would you like an example to clarify it further?
06:30:08
Öğrenci
I got it
06:30:10
💭 AI Öğretmen
Let us proceed carefully
06:30:11
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:32:27
Öğrenci
My answer is: Domain:{-1, 0, 1, 2,} Codomain:{0, 1, 2, 3, 4, 5} Range:{0, 1, 4}
06:32:28
💭 AI Öğretmen
Noted your answer
06:32:33
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range of the function!
06:32:35
AI Öğretmen
Your answer shows a great understanding of how to interpret these sets from a mapping diagram.
06:32:36
AI Öğretmen
Remember, the domain is all possible inputs, the codomain is all possible outputs, and the range is the set of actual outputs that the function produces.
06:32:37
AI Öğretmen
Keep up the excellent work!
06:32:40
AI Öğretmen
Therefore, the correct answer is Domain: $\\{-1, 0, 1, 2\\}$, Codomain: $\\{0, 1, 2, 3, 4, 5\\}$, Range: $\\{0, 1, 4\\}$
06:32:40
AI Öğretmen
Should we continue with the lecture?
06:33:07
Öğrenci
Alright, let's continue
06:33:08
💭 AI Öğretmen
Moving forward now
06:33:17
Görsel
Görsel
06:33:21
AI Öğretmen
A relation is called a function if it meets an important rule: each input (from the Domain or Set A) is linked to some output in the Codomain (Set B).
06:33:23
AI Öğretmen
This means that for every element in the domain, there is a single matching element in the codomain.
06:33:26
AI Öğretmen
It is important to note that not every element in the codomain has to be matched to something from the domain, so some codomain elements can be left unused.
06:33:27
AI Öğretmen
Also, it is allowed for different inputs to share the same output; this is called a many-to-one mapping.
06:33:29
AI Öğretmen
However, a single input cannot be assigned to more than one output. In other words, one-to-many mappings are not permitted in functions.
06:33:30
AI Öğretmen
So, a function is a relation that gives exactly one output in the codomain for each input from the domain.
06:33:31
AI Öğretmen
Did you understand how a function relates inputs to outputs?
06:34:11
Öğrenci
I got it
06:34:13
💭 AI Öğretmen
Now, let us review this question
06:34:13
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:34:44
Öğrenci
My answer is: not a function
06:34:45
💭 AI Öğretmen
Noted your answer
06:34:50
AI Öğretmen
That's absolutely right! Fantastic job!
06:34:52
AI Öğretmen
You correctly identified that this relation is not a function because for some natural numbers in the domain, like 1 or 2, the result of $f(x) = x - 3$ would be a negative number.
06:34:54
AI Öğretmen
Since negative numbers are not in the set of natural numbers (the codomain), not every input has a valid output, which is a key requirement for a function.
06:34:54
AI Öğretmen
Keep up the great work understanding domains and codomains!
06:34:55
AI Öğretmen
Therefore, the correct answer is not a function.
06:34:55
AI Öğretmen
Should we continue with the lecture?
06:35:23
Öğrenci
Alright, let's continue
06:35:24
💭 AI Öğretmen
Moving to next section
06:35:29
Görsel
Görsel
06:35:32
AI Öğretmen
A relation between two sets can be analyzed to determine if it is a function by checking specific rules.
06:35:34
AI Öğretmen
Consider two sets: Set A, called Inputs, which is $\{1, 2, 3\}$, and Set B, called Outputs, which is $\{10, 20\}$.
06:35:35
AI Öğretmen
The mappings between these sets are as follows: $1 \to 10$, $2 \to 10$, and $3 \to 20$.
06:35:38
AI Öğretmen
Here, each element from Set A—1, 2, and 3—has a mapping: 1 is paired with 10, 2 is paired with 10, and 3 is paired with 20.
06:35:39
AI Öğretmen
All the inputs from Set A are assigned to an output, and each input has only one output.
06:35:42
AI Öğretmen
It is allowed that different inputs can have the same output; for example, both 1 and 2 map to 10 in this relation.
06:35:44
AI Öğretmen
In conclusion, this relation is a function because every element in the domain maps to exactly one element in the codomain.
06:35:45
AI Öğretmen
Did you understand why this relation qualifies as a function?
06:36:27
Öğrenci
I got it
06:36:30
💭 AI Öğretmen
Let us review this topic
06:36:30
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:38:17
Öğrenci
My answer is: the largest domain:x-(-2)
06:38:17
💭 AI Öğretmen
Let's review that carefully
06:38:23
AI Öğretmen
Your answer was not correct, let me explain why. The domain of a function tells us all the possible input values (x-values) for which the function works without any problems.
06:38:25
AI Öğretmen
For the function \( f(x) = \frac{4}{x+2} \), the problem happens when the denominator equals zero, because division by zero is undefined.
06:38:28
AI Öğretmen
So, we set \( x + 2 \neq 0 \), which means \( x \neq -2 \). This tells us the function is defined for all real numbers except \( -2 \).
06:38:30
AI Öğretmen
A common mistake is to write something like "x - (-2)" which is just an expression, not a description of the domain. The domain should be expressed as all real numbers except \( -2 \), like this: \(\{x \in \mathbb{R} \mid x \neq -2\}\).
06:38:33
AI Öğretmen
For example, if you plug in \( x = 0 \), the function works fine: \( f(0) = \frac{4}{0+2} = 2 \). But if you try \( x = -2 \), the denominator becomes zero and the function is not defined.
06:38:34
AI Öğretmen
Therefore, the correct answer should be the set of all real numbers except \( -2 \), written as \(\{x \in \mathbb{R} \mid x \neq -2\}\).
06:38:35
AI Öğretmen
Should we continue with the lecture?
06:39:42
Öğrenci
Alright, let's continue
06:39:43
💭 AI Öğretmen
Moving forward now
06:39:51
AI Öğretmen
A relation is considered a function if and only if each input value from the domain matches to one and only one output value in the codomain.
06:39:54
AI Öğretmen
This means that no input has more than one output, but it is completely fine for multiple inputs to share the same output.
06:39:54
AI Öğretmen
In other words, each starting value points to a single result, but some results can be pointed to by more than one starting value.
06:39:55
AI Öğretmen
Does it make sense to you that each input must have only one output for a relation to be a function?
06:40:24
Öğrenci
I got it
06:40:26
💭 AI Öğretmen
let's check your understanding
06:40:27
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:40:53
Öğrenci
My answer is: 18
06:40:55
💭 AI Öğretmen
Let me review that answer
06:40:59
AI Öğretmen
That's absolutely correct! Fantastic job!
06:41:00
AI Öğretmen
You correctly figured out that to find $f(3)$, you needed to set $x-1$ equal to 3, which gave you $x=4$.
06:41:02
AI Öğretmen
Then, by substituting $x=4$ into $4x+2$, you accurately calculated the value of the function. This shows a great understanding of function evaluation!
06:41:03
AI Öğretmen
Therefore, the correct answer is 18.
06:41:04
AI Öğretmen
Should we continue with the lecture?
06:41:25
Öğrenci
Alright, let's continue
06:41:26
💭 AI Öğretmen
Moving forward now
06:41:37
AI Öğretmen
In this lesson, we covered the definition of a function as a relation where every input in the domain maps to exactly one output in the codomain. We also discussed the concepts of domain, codomain, and range, and how to determine if a relation is a function by checking these mappings. Additionally, we looked at examples to understand how different inputs can share the same output, but one input cannot have multiple outputs. Do you have any questions about these topics? If not, I'll end the lesson.
06:43:25
Öğrenci
finish lesson
06:43:29
AI Öğretmen
See you in the next lesson!

Voltran Okul Analiz Sistemi