← Ana Rapor / Giz Derin TAŞ / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:52
Bitiş
Devam ediyor
Süre
9 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
  • One to One Function
Kazanımlar:
  • 2.1.d. One to One Function

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci derse konunun detaylı bir şekilde anlatılmasını isteyerek başladı. Bu, konuya dair ön bilgisinin az olduğunu veya kendine güvenmediğini göstermektedir.

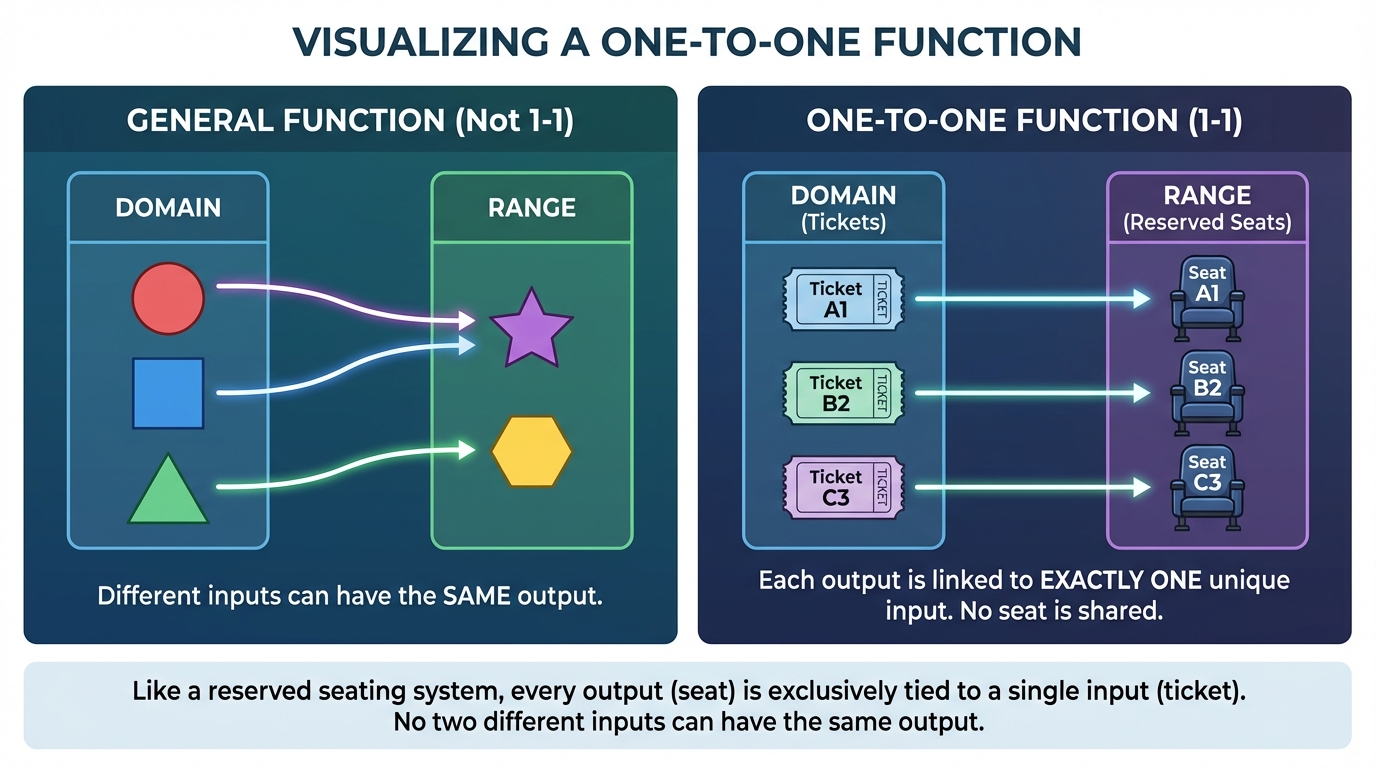
- Başlangıç: İlk başta, şema ile gösterilen bir fonksiyonun bire bir olup olmadığını doğru bir şekilde tespit etti ve mantığını da ("iki farklı girdinin aynı çıktıya sahip olması") doğru açıkladı. Bu, kavramın görsel temsilini anladığına dair olumlu bir işaretti.
- Zorlukların Başlaması: Ancak, konu cebirsel ifadelere geldiğinde öğrenci zorlanmaya başladı. `f(x) = 5x - 9` fonksiyonu sorulduğunda önce ipucu istedi, ipucu aldıktan sonra ise yanlış cevap verdi. Bu durum, öğrencinin görsel temsilleri anlarken, fonksiyonları cebirsel olarak analiz etme ve bire bir olma durumunu test etme konusunda zorlandığını gösteriyor.
- Anlama Eksikliğinin Derinleşmesi: Yanlış cevabından sonra konunun nasıl çözüleceğine dair genel bir soru sorması ("how do i determine it with questions like the previous one") ve ardından verilen alıştırma sorularının hiçbirini çözemeyip "Can you solve it I can't understand" demesi, konuyu temelden anlamadığını net bir şekilde ortaya koymaktadır.

Sonuç olarak, öğrenci bire bir fonksiyon kavramının sadece en temel ve görsel düzeydeki tanımını anlamış görünmektedir. Ancak, bir fonksiyonun (özellikle doğrusal fonksiyonların) bire bir olup olmadığını cebirsel olarak belirleme konusunda ciddi eksiklikleri vardır. Konunun tekrar edilmesi ve farklı soru tipleriyle pekiştirilmesi gerekmektedir.

Konu ve Kazanım Analizi

# Eksiklik Tespit Edilen Konular (Topics with Gaps)
* Introduction to Functions and Linear Functions

# Eksiklik Tespit Edilen Alt Konular (Subtopics with Gaps)
* One to One Function

# Eksiklik Tespit Edilen Kazanımlar (Outcomes with Gaps)
* 2.1.d. One to One Function

# İyi Olduğu Konular (Topics Good At)
* *Bu derste öğrencinin baştan sona sorunsuz anladığı bir konu tespit edilmemiştir.*

# İyi Olduğu Alt Konular (Subtopics Good At)
* *Bu derste öğrencinin baştan sona sorunsuz anladığı bir alt konu tespit edilmemiştir.*

Ders Dışı Sorular/Yorumlar
* *Ders dışı herhangi bir yorum veya soru kaydedilmemiştir.*

📜 Oturum Detayları

06:52:33
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:52:34
💭 AI Öğretmen
Of course, preparing details now
06:52:34
Görsel
Görsel
06:52:37
AI Öğretmen
A one-to-one function, which is also called a 1-1 function, is a special kind of function with a strict rule about how inputs and outputs connect.
06:52:38
AI Öğretmen
In most functions, two different input values might give you the same output value, but in a one-to-one function, this is not allowed.
06:52:40
AI Öğretmen
For a one-to-one function, each output matches up with just one unique input, so no output comes from two different inputs.
06:52:41
AI Öğretmen
You can imagine it like a reserved seating system at a movie theater, where each ticket is for exactly one seat, and no two tickets let you sit in the same seat.
06:52:43
AI Öğretmen
So in function terms, each output is matched to just one input, and every output value comes from at most one starting value in the domain.
06:52:45
AI Öğretmen
This rule keeps every output linked only to a single input, which makes these functions more strict than regular functions.
06:52:46
AI Öğretmen
Did you understand how a one-to-one function pairs each output with a unique input?
06:53:35
Öğrenci
I got it
06:53:38
💭 AI Öğretmen
Let's review this question.
06:53:38
❓ Soru basic
Determine whether the following function is one-to-one: ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_185ba90c-a01e-449e-9b2f-98a502915e79.png)
06:54:21
Öğrenci
My answer is: this isn't a one to one function because two different inputs are matched with the same output
06:54:23
💭 AI Öğretmen
Noted your explanation
06:54:28
AI Öğretmen
Fantastic job! You've absolutely nailed it!
06:54:30
AI Öğretmen
You correctly identified that this function is not one-to-one because two different inputs, 'b' and 'c', are both mapped to the same output, 'y'.
06:54:32
AI Öğretmen
Remember, for a function to be one-to-one, every unique input must correspond to a unique output. Keep up the great work!
06:54:32
AI Öğretmen
Therefore, the function is not one-to-one.
06:54:33
AI Öğretmen
Should we continue with the lecture?
06:54:52
Öğrenci
Alright, let's continue
06:54:53
💭 AI Öğretmen
Moving forward now
06:54:59
🎥 Video
06:54:59
AI Öğretmen
Did you understand how the one-to-one property of a function works?
06:55:39
Öğrenci
I got it
06:55:43
💭 AI Öğretmen
Let us review this.
06:55:43
❓ Soru basic
**Example:** Determine whether the function $f: \mathbb{R} \to \mathbb{R}, f(x) = 5x - 9$ is one to one or not. Explain your reasoning.
06:56:13
Öğrenci
Can you give me a hint, teacher?
06:56:14
💭 AI Öğretmen
Let me review that
06:56:17
AI Öğretmen
What would happen if you tried to find two different inputs, say \(x_1\) and \(x_2\), that give the same output when plugged into the function \(f(x) = 5x - 9\)?
06:56:19
AI Öğretmen
How could you set up an equation to test whether \(f(x_1) = f(x_2)\) implies that \(x_1 = x_2\)?
06:56:20
AI Öğretmen
Why do you think it is important that different inputs do or do not produce the same output in determining if a function is one-to-one?
06:57:03
Öğrenci
My answer is: this is not a one to one function
06:57:04
💭 AI Öğretmen
Let me consider that carefully
06:57:10
AI Öğretmen
Your answer was not correct, let me explain why the function \( f(x) = 5x - 9 \) is actually one-to-one.
06:57:14
AI Öğretmen
A function is one-to-one if every different input \( x \) gives a different output \( f(x) \). This means if \( f(x_1) = f(x_2) \), then \( x_1 \) must equal \( x_2 \).
06:57:18
AI Öğretmen
For this function, if we assume \( f(x_1) = f(x_2) \), then \( 5x_1 - 9 = 5x_2 - 9 \). Adding 9 to both sides gives \( 5x_1 = 5x_2 \), and dividing by 5 leads to \( x_1 = x_2 \).
06:57:21
AI Öğretmen
This shows that no two different inputs produce the same output, so the function is one-to-one. A common misconception is thinking linear functions are not one-to-one, but if the slope (here 5) is not zero, the function is strictly increasing or decreasing and thus one-to-one.
06:57:23
AI Öğretmen
For example, \( f(1) = 5(1) - 9 = -4 \) and \( f(2) = 5(2) - 9 = 1 \), which are different outputs for different inputs.
06:57:25
AI Öğretmen
Therefore, the correct answer should be that the function \( f(x) = 5x - 9 \) is one-to-one.
06:57:25
AI Öğretmen
Should we continue with the lecture?
06:58:27
Öğrenci
Alright, let's continue
06:58:27
💭 AI Öğretmen
Moving to next example
06:58:33
🎥 Video
06:58:33
AI Öğretmen
Did this example help you understand the difference between one-to-one and not one-to-one relationships?
06:59:16
Öğrenci
how do i determine it with questions like the previous one
06:59:18
💭 AI Öğretmen
Let me check that for you
06:59:23
AI Öğretmen
To determine if a function is one-to-one, ask: "Can two different inputs give the same output?" If yes, it’s not one-to-one; if no, it is one-to-one.
06:59:25
AI Öğretmen
For example, check if \( f(x_1) = f(x_2) \) implies \( x_1 = x_2 \). If this is always true, the function is one-to-one.
06:59:27
AI Öğretmen
Think about real-life examples like fingerprints (one-to-one) versus birth months (not one-to-one) to help understand the concept.
06:59:28
AI Öğretmen
Do you want me to explain this with more examples or practice questions?
06:59:57
Öğrenci
practice questions
07:00:00
💭 AI Öğretmen
Let me prepare that
07:00:03
AI Öğretmen
Sure! Here are some practice questions for you: 1. Is the function \( f(x) = 2x + 3 \) one-to-one? Explain why or why not.
07:00:05
AI Öğretmen
2. Consider the function \( g(x) = x^2 \). Is \( g \) one-to-one on the domain of all real numbers? Why?
07:00:07
AI Öğretmen
3. Think about the relationship between a student and their student ID number. Is this a one-to-one relationship? Explain.
07:00:09
AI Öğretmen
Try these and let me know if you want me to check your answers or explain any of them!
07:01:08
Öğrenci
Can you solve it I can't understand.
07:01:12
💭 AI Öğretmen
Let us review the topic again
07:01:12
Görsel
Görsel
07:01:15
AI Öğretmen
Let's look at what a one-to-one relationship means by thinking about people and their fingerprints.
07:01:16
AI Öğretmen
In this example, you start with a person as your input, and then find their fingerprint as the output.
07:01:17
AI Öğretmen
This is called one-to-one because every person has only one unique fingerprint pattern, and no two people have the same fingerprint.
07:01:18
AI Öğretmen
So, the set of all people is called the domain, and the set of fingerprint patterns is the range.
07:01:19
AI Öğretmen
This means each person matches with only their fingerprint—never someone else's.
07:01:20
AI Öğretmen
Now, let's think about a different example, where the input is still people, but the output is their birth month.
07:01:21
AI Öğretmen
If you check people and their birth months, you will see that many people can have the same birth month, like January or June.

Voltran Okul Analiz Sistemi