← Ana Rapor / Alya Deniz USTA / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:42
Bitiş
Devam ediyor
Süre
12 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Kazanımlar:
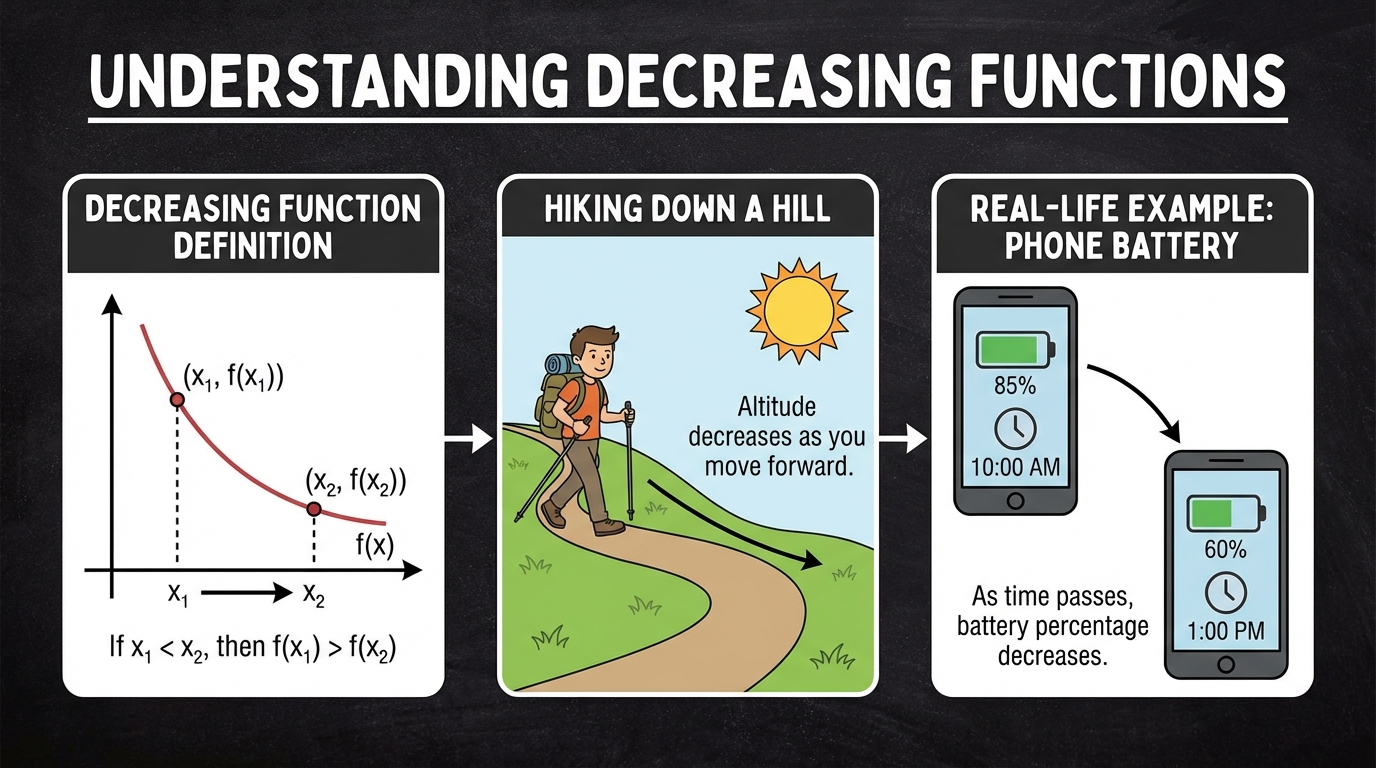
  • 2.1.c. Increasing and Decreasing Intervals of a Function

Detaylı Değerlendirme

Öğrenci Performans Analizi

Bu derste öğrencinin performansı değişkenlik göstermiştir. Öğrenci, artan ve azalan aralıkları grafik üzerinden tekil olarak belirleme konusunda başarılı bir başlangıç yapmıştır. Ancak, dersin sonunda birden fazla kavramı (artan, azalan, sabit aralıklar ve maksimum değer) bir arada kullanması gereken soruda zorlanmıştır.

# Genel Değerlendirme
- Başlangıç: Öğrenci, dersin başında artan ve azalan aralıklarla ilgili sorulan tekil soruları doğru bir şekilde cevaplamıştır. Bu, temel kavramları anladığını göstermektedir.
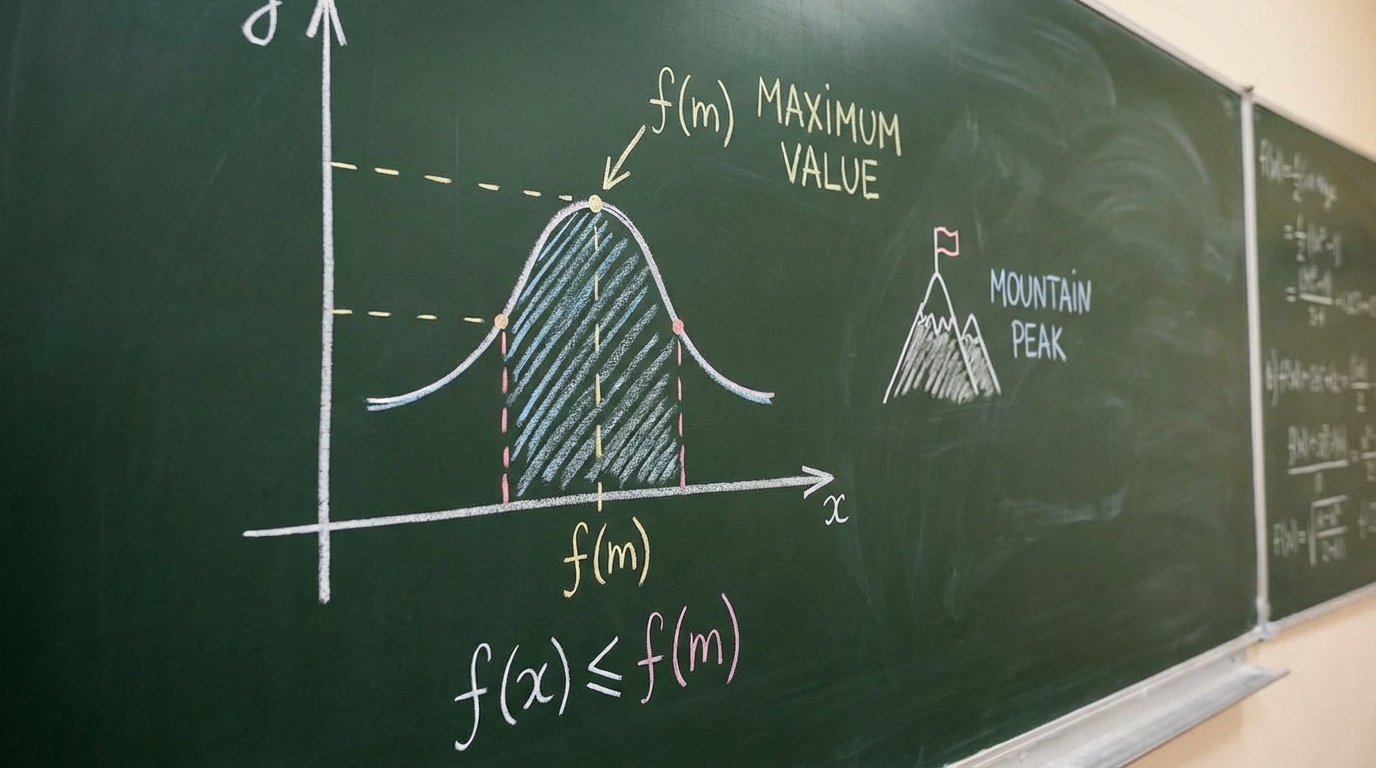
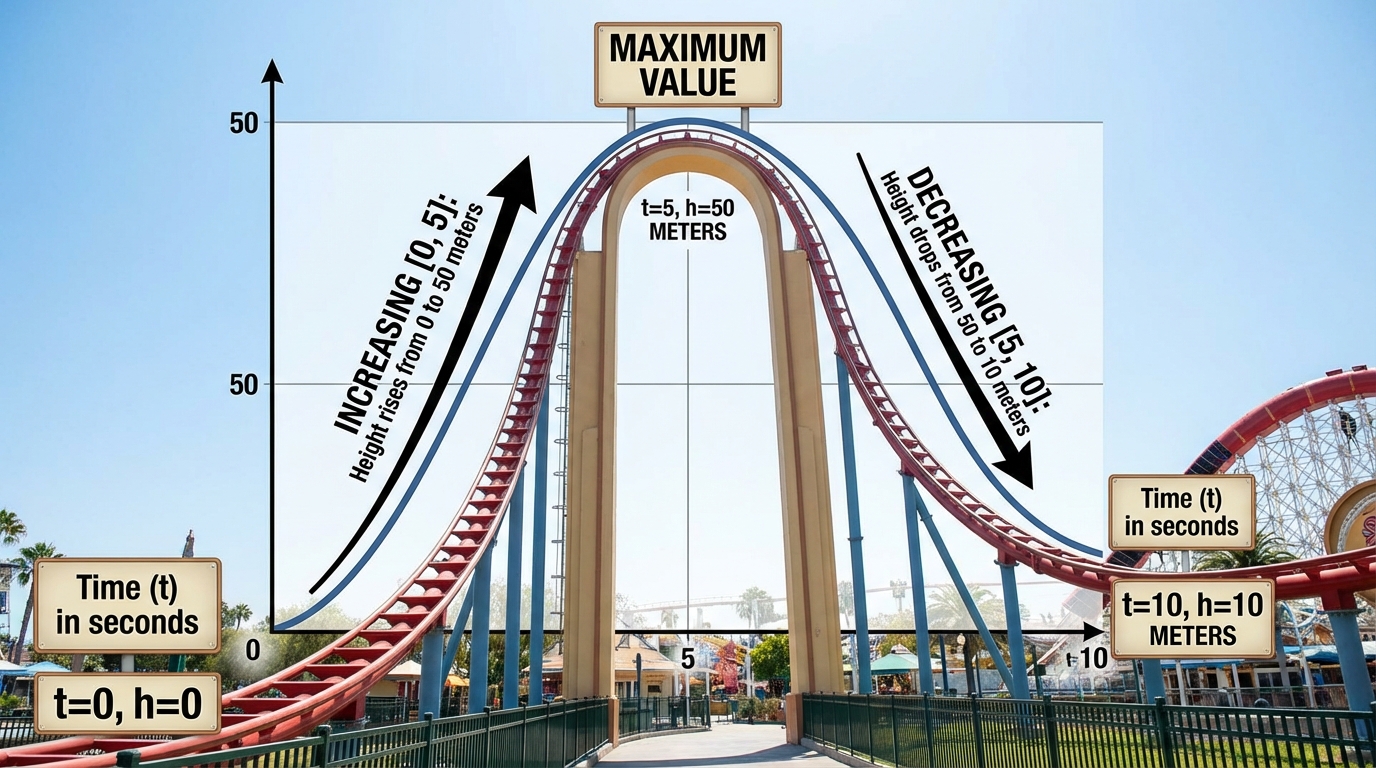
- Zorlandığı Noktalar: Dersin sonundaki birleşik soruda, grafikteki tüm aralıkları doğru bir şekilde belirlemesine rağmen sorunun "maksimum değeri bulma" kısmını tamamen atlamıştır. Bu durum, öğrencinin ya soruyu eksik okuduğunu ya da yeni öğrenilen "maksimum değer" kavramını mevcut bilgileriyle birleştirmekte zorlandığını göstermektedir.
- Öğrenme Stili: Öğrenci, "Anladım" diyerek hızlıca ilerlese de, karmaşık bir soruyla karşılaştığında eksik cevap vermesi, konuları tam olarak içselleştirmeden ilerlediğine işaret edebilir.

Detaylı Analiz

# İyi Olduğu Konular
Öğrenci, bir fonksiyon grafiğinde artan ve azalan aralıkların neresi olduğunu görsel olarak tespit etme konusunda başarılıdır. Bu konulardaki ilk sorulara tereddütsüz ve doğru yanıtlar vermiştir.

# Eksik Olduğu Konular
Öğrencinin temel eksikliği, birden çok talimat içeren veya birden fazla kavramı birleştiren soruları yanıtlarken ortaya çıkmıştır. Özellikle, sorunun tüm bileşenlerini dikkatli bir şekilde okuyup cevaplama ve yeni öğrenilen bir kavramı (maksimum değer) uygulama konusunda zayıflık göstermiştir. Bu nedenle ilgili kazanım, karma performans gösterildiği için eksiklikler listesine eklenmiştir.

# Ders Dışı Sorular/Yorumlar
- "How do we find the maximum value of a function using derivatives?" (Bir fonksiyonun maksimum değerini türev kullanarak nasıl buluruz?)
- Bu soru, dersin kapsamı (grafik okuma) dışında olmasına rağmen konuyla ilgili bir merakı göstermektedir.

📜 Oturum Detayları

06:42:49
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:42:50
💭 AI Öğretmen
Preparing detailed explanation
06:42:50
Görsel
Görsel
06:42:52
AI Öğretmen
Graphs in math are read from left to right, just like you read a sentence in English.
06:42:54
AI Öğretmen
This way of looking at graphs helps us understand how a function behaves as we move along the $x$-axis.
06:42:55
AI Öğretmen
When you compare two $x$-values on a graph, you always move from the left point to the right point.
06:42:56
AI Öğretmen
Using this direction, you can see if the function goes up (increases) or goes down (decreases) between those points.
06:42:57
AI Öğretmen
Remembering to look from left to right makes it easier to know when the function is increasing or decreasing.
06:42:58
AI Öğretmen
Did you understand how the left-to-right reading helps us identify increasing and decreasing intervals on a graph?
06:43:42
Öğrenci
I got it
06:43:44
💭 AI Öğretmen
Good, moving forward
06:43:45
🎥 Video
06:43:45
AI Öğretmen
Did you understand how an increasing interval of a function works?
06:44:32
Öğrenci
I got it
06:44:34
💭 AI Öğretmen
Let us reinforce this topic
06:44:34
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_33e16c0c-dc3a-47bd-91c9-e1d47eecd95c.png) Example: The graph of f is shown on the below. Find the intervals of x for which f(x) is **increasing**.
06:45:32
Öğrenci
My answer is: [ -5,-2] U [0.3]
06:45:33
💭 AI Öğretmen
Reviewing your answer now
06:45:36
AI Öğretmen
Fantastic job! You've correctly identified the intervals where the function is increasing.
06:45:37
AI Öğretmen
Your answer is spot on because you recognized where the graph moves upwards as you read it from left to right.
06:45:38
AI Öğretmen
Remember, an increasing function means that as the x-values get larger, the y-values also get larger, which you clearly understood!
06:45:39
AI Öğretmen
Therefore, the correct answer is $[-5, -2] \cup [0, 3]$.
06:45:40
AI Öğretmen
Should we continue with the lecture?
06:46:06
Öğrenci
Alright, let's continue
06:46:06
💭 AI Öğretmen
Moving forward now
06:46:13
Görsel
Görsel
06:46:16
AI Öğretmen
A function is decreasing on an interval if, for any $x_1 < x_2$ in that interval, $f(x_1) > f(x_2)$.
06:46:18
AI Öğretmen
You can picture this like hiking down a hill, where your altitude gets lower as you keep moving forward.
06:46:19
AI Öğretmen
Another example is your phone's battery percentage, which gets smaller as time passes during the day, showing a real-life decreasing function.
06:46:20
AI Öğretmen
Does this explanation about decreasing functions make sense to you?
06:46:46
Öğrenci
I got it
06:46:48
💭 AI Öğretmen
Let's review this carefully
06:46:48
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_fb69fa74-e294-4d91-a021-e549025bd3c4.png) Example: The graph of $f$ is shown on the above. Find the intervals of $x$ for which $f(x)$ is **decreasing**.
06:47:07
Öğrenci
My answer is: [-2,0]
06:47:08
💭 AI Öğretmen
Reviewing your answer now
06:47:12
AI Öğretmen
That's absolutely correct! Fantastic job!
06:47:13
AI Öğretmen
You correctly identified that a function is decreasing when its graph goes downwards as you move from left to right.
06:47:15
AI Öğretmen
Your answer shows you understand how to analyze a graph to find intervals where the function's values are getting smaller.
06:47:17
AI Öğretmen
Keep up the great work!
06:47:18
AI Öğretmen
Therefore, the correct answer is [-2, 0].
06:47:18
AI Öğretmen
Should we continue with the lecture?
06:47:36
Öğrenci
Alright, let's continue
06:47:37
💭 AI Öğretmen
Proceeding to next section
06:47:44
Görsel
Görsel
06:47:47
AI Öğretmen
The maximum value of a function is the highest output it attains within a given interval.
06:47:48
AI Öğretmen
Mathematically, $f(m)$ is called the maximum if, for every $x$ in the interval, $f(x) \leq f(m)$.
06:47:49
AI Öğretmen
This definition refers to the highest value on the specified interval, known as the absolute maximum for that interval.
06:47:52
AI Öğretmen
On a graph, this maximum appears as the very top or "peak" point, where the function stops rising and starts falling.
06:47:53
AI Öğretmen
Not every function has a maximum in every interval, but when it does, it looks visually like the top of a mountain.
06:47:53
AI Öğretmen
Did the explanation about the maximum value of a function make sense to you?
06:48:36
Öğrenci
How do we find the maximum value of a function using derivatives?
06:48:40
💭 AI Öğretmen
Let me explain that clearly
06:48:44
AI Öğretmen
To find the maximum value of a function using derivatives, you first find the critical points by setting the derivative $f'(x)$ equal to zero.
06:48:45
AI Öğretmen
These points are where the function's slope is zero, meaning the graph could have a peak (maximum), valley (minimum), or a flat spot.
06:48:47
AI Öğretmen
Next, you use the second derivative test: if $f''(x) < 0$ at a critical point, the function has a local maximum there.
06:48:49
AI Öğretmen
Finally, compare the function values at these points and the interval boundaries to find the absolute maximum.
06:48:50
AI Öğretmen
Does this explanation about using derivatives to find maxima make sense to you?
06:49:42
Öğrenci
I got it
06:49:44
💭 AI Öğretmen
Let us review this briefly
06:49:45
❓ Soru basic
**Example:** The graph of $g$ is shown below. Find the intervals of $x$ for which $g(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?** ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_11a805a3-b66d-431d-99b4-450c738ea61d.png)
06:52:33
Öğrenci
My answer is: constant (-2,1),increasing: [1,3] U [-5,-2] Decreasing: [3,6]
06:52:34
💭 AI Öğretmen
Let me review that answer
06:52:38
AI Öğretmen
Your answer was not correct because you missed including the maximum value of the function, which is an important part of the question.
06:52:39
AI Öğretmen
Let's break it down step-by-step: the function is constant where the graph is flat, which is between x = -2 and x = 1, so the interval should be written as [-2, 1].
06:52:41
AI Öğretmen
The function increases when the graph goes upward. This happens from x = -5 to -2 and from x = 1 to 3, so the increasing intervals are [-5, -2] and [1, 3].
06:52:42
AI Öğretmen
The function decreases when the graph goes downward, which is from x = 3 to 6, so the decreasing interval is [3, 6].
06:52:44
AI Öğretmen
Finally, the maximum value of the function is the highest point on the graph, which is y = 3 at x = 3. This was missing from your answer.
06:52:45
AI Öğretmen
A common mistake is forgetting to answer all parts of the question or mixing up open and closed intervals; here, the intervals include the endpoints where the behavior changes, so brackets [] are used.
06:52:48
AI Öğretmen
Therefore, the correct maximum value should be 3, and the intervals are constant on [-2, 1], increasing on [-5, -2] and [1, 3], and decreasing on [3, 6].
06:52:48
AI Öğretmen
Should we continue with the lecture?
06:54:17
Öğrenci
Alright, let's continue
06:54:17
💭 AI Öğretmen
Let us proceed further
06:54:23
Görsel
Görsel
06:54:25
AI Öğretmen
Think of a rollercoaster example, where t stands for time and h stands for height.
06:54:27
AI Öğretmen
This means the function shows the relationship between height and time.
06:54:29
AI Öğretmen
The function is increasing on the interval $[0,5]$ because the height goes up from 0 meters to 50 meters as time increases from 0 to 5 seconds.
06:54:31
AI Öğretmen
At $t=5$ seconds, the function reaches its maximum value, which is 50 meters.
06:54:33
AI Öğretmen
After that, the function is decreasing on the interval $[5,10]$, because the height falls from 50 meters to 10 meters between 5 and 10 seconds.
06:54:36
AI Öğretmen
When we state intervals like $[0,5]$ and $[5,10]$, it becomes clear exactly when the function is increasing and when it is decreasing.
06:54:37
AI Öğretmen
Did you understand how the intervals show when the function is increasing or decreasing?

Voltran Okul Analiz Sistemi