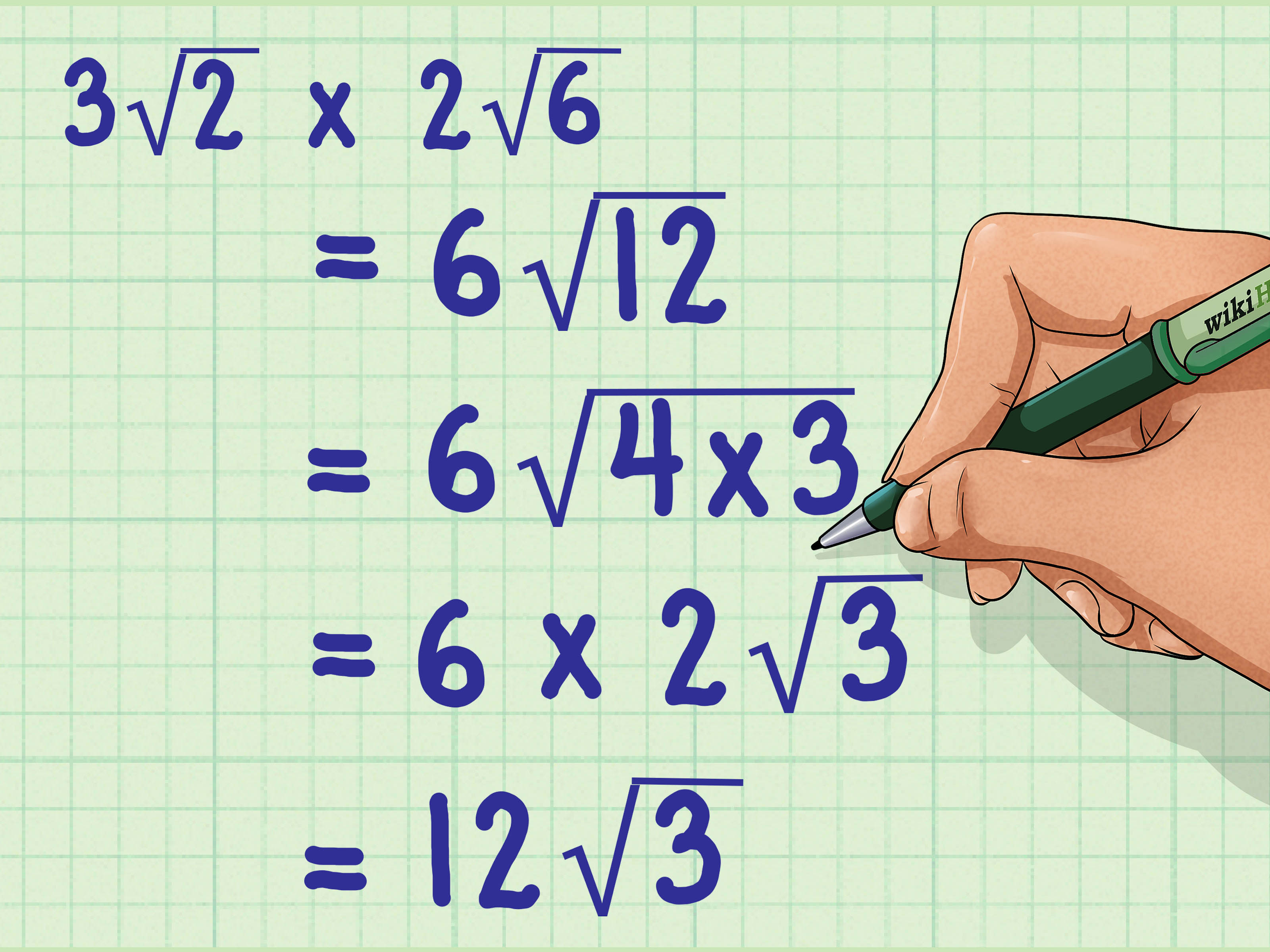← Ana Rapor / Alya CESUR / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
24 October 2025, 05:39
Bitiş
Devam ediyor
Süre
21 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Operations with Exponential and Radical Representations of Real Numbers
Alt Konular:
  • Radicals
Kazanımlar:
  • Ability to reason about operations with exponential and radical representations of real numbers

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, dersin başında konunun detaylı anlatılmasını isteyerek öğrenmeye istekli olduğunu göstermiştir. Ancak, ders boyunca köklü sayılarla ilgili temel işlemlerde zorlandığı gözlemlenmiştir.

# Güçlü Yönler
Öğrenci, köklü ifadelerin çarpımı konusunda başarılı bir performans sergilemiştir. Özellikle dağılma özelliğini doğru bir şekilde uygulamış ve `√x * √x` ifadesinin `x`'e eşit olduğunu doğru bir şekilde bularak işlemi tamamlamıştır. Bu, köklü ifadelerle çarpma işleminin temel mantığını anladığını göstermektedir.

# Geliştirilmesi Gereken Yönler
Öğrencinin en belirgin eksiklikleri iki ana noktada toplanmaktadır:
1. Köklü İfadeleri Üslü Biçimde Yazma: Kendisinden `√(x²)` ifadesini üslü biçimde yazması istendiğinde, ifadeyi sadeleştirerek `x` cevabını vermiştir. Bu durum, "üslü biçimde yazma" ile "ifadeyi sadeleştirme" arasındaki farkı tam olarak anlamadığını göstermektedir.
2. Köklü İfadelerle Toplama ve Çıkarma: `√27 + √48 - √12` işlemi sorulduğunda, terimlerin hepsini sadeleştirip ortak kök parantezinde toplamak yerine sadece bir terimin sadeleştirilmesi gerektiğini belirtmiş ancak işlemi tamamlayamamıştır. Bu, toplama ve çıkarma yapabilmek için kök içlerinin aynı olması gerektiği ve bunun için her bir terimin ayrı ayrı sadeleştirilmesi gerektiği bilgisinin tam oturmadığını göstermektedir.

Öğrenci, her konsept anlatımından sonra "Anladım" demesine rağmen, takip eden sorularda yanlış cevaplar vermiştir. Bu durum, konuyu teoride anladığını düşünse de pratikte uygulamada zorlandığını göstermektedir.

📜 Oturum Detayları

05:39:45
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
05:39:46
💭 AI Öğretmen
Preparing detailed explanation
05:39:46
🎥 Video
05:39:46
AI Öğretmen
Did you understand how simplifying radicals helps in performing arithmetic operations with them?
05:40:42
Öğrenci
I got it
05:40:46
💭 AI Öğretmen
Now, let's proceed
05:40:46
❓ Soru basic
$\sqrt{x^2}$ Write the expression in exponential form
05:40:58
Öğrenci
My answer is: x
05:40:59
💭 AI Öğretmen
Noted your answer
05:41:03
AI Öğretmen
Your answer was not correct, let me explain why.
05:41:04
AI Öğretmen
The question asked you to write the expression \(\sqrt{x^2}\) in exponential form, which means expressing the square root using exponents rather than simplifying the whole expression.
05:41:05
AI Öğretmen
To convert a square root to exponential form, remember that \(\sqrt{A} = A^{\frac{1}{2}}\). So, \(\sqrt{x^2}\) becomes \((x^2)^{\frac{1}{2}}\).
05:41:08
AI Öğretmen
Next, you can simplify the exponent using the power of a power rule: \((a^m)^n = a^{m \cdot n}\). Applying this gives \((x^2)^{\frac{1}{2}} = x^{2 \times \frac{1}{2}} = x^1 = x\).
05:41:09
AI Öğretmen
However, since the question specifically asked for the expression in exponential form, the correct answer should be \((x^2)^{\frac{1}{2}}\), not just \(x\).
05:41:10
AI Öğretmen
A common confusion is to simplify the expression completely instead of just rewriting it in exponential form. Keep in mind the difference between rewriting an expression and simplifying it.
05:41:12
AI Öğretmen
Therefore, the correct answer should be \((x^2)^{\frac{1}{2}}\). Keep practicing, and you'll get even better at recognizing what the question asks for!
05:41:12
AI Öğretmen
Should we continue with the lecture?
05:46:36
Öğrenci
Alright, let's continue
05:46:37
💭 AI Öğretmen
Proceeding to next part
05:46:57
🎥 Video
05:46:57
AI Öğretmen
Did you understand how to add and subtract radicals after simplifying them?
05:48:19
Öğrenci
I got it
05:48:21
💭 AI Öğretmen
Let us review carefully
05:48:21
❓ Soru medium
A student was asked to simplify the expression $\sqrt{27} + \sqrt{48} - \sqrt{12}$. Their work is shown below: Step 1: Simplify $\sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3}$ Step 2: Simplify $\sqrt{48} = \sqrt{16 \cdot 3} = 4\sqrt{3}$ Step 3: Combine the first two terms: $3\sqrt{3} + 4\sqrt{3} = 7\sqrt{3}$ Step 4: Final Answer: $7\sqrt{3} - \sqrt{12}$ The student's final answer is incorrect because it is not fully simplified. Identify the student's procedural error and provide the correct, final answer.
05:49:51
Öğrenci
My answer is: the student should simplify root 12 to a root b to finalize the calculation
05:49:53
💭 AI Öğretmen
Let me review that
05:49:56
AI Öğretmen
Your answer was not correct, let me explain why.
05:49:58
AI Öğretmen
The main issue is that you recognized the need to simplify \(\sqrt{12}\), but you didn't actually perform the simplification or complete the calculation to get the final answer.
05:50:00
AI Öğretmen
Let's go step-by-step to clarify the process: First, simplify every square root in the expression \(\sqrt{27} + \sqrt{48} - \sqrt{12}\).
05:50:02
AI Öğretmen
\(\sqrt{27} = \sqrt{9 \times 3} = 3\sqrt{3}\), \(\sqrt{48} = \sqrt{16 \times 3} = 4\sqrt{3}\), and \(\sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3}\).
05:50:03
AI Öğretmen
Now rewrite the expression using these simplified forms: \(3\sqrt{3} + 4\sqrt{3} - 2\sqrt{3}\).
05:50:04
AI Öğretmen
Since all terms have the same radical \(\sqrt{3}\), you can combine their coefficients: \(3 + 4 - 2 = 5\).
05:50:05
AI Öğretmen
So, the fully simplified answer is \(5\sqrt{3}\).
05:50:06
AI Öğretmen
The key takeaway is to always simplify all radicals before combining like terms, so you can see if they have the same radical part.
05:50:08
AI Öğretmen
Therefore, the correct answer should be \(5\sqrt{3}\). Keep practicing, and you'll get more comfortable with these steps!
05:50:08
AI Öğretmen
Should we continue with the lecture?
05:51:54
Öğrenci
Alright, let's continue
05:51:55
💭 AI Öğretmen
Let us proceed now
05:52:03
Görsel
Görsel
05:52:06
AI Öğretmen
Multiplying radicals is different from adding or subtracting them; the radicals do not have to be the same for multiplication.
05:52:07
AI Öğretmen
There are three main steps to follow when you multiply radicals.
05:52:08
AI Öğretmen
First, you multiply the coefficients, which are the numbers in front of the radical signs.
05:52:09
AI Öğretmen
Second, you multiply the radicands, which are the numbers inside the radical signs, by using the Product Rule.
05:52:10
AI Öğretmen
Third, you simplify the radical if you can, by looking for perfect squares, cubes, or any common factors inside the radical.
05:52:12
AI Öğretmen
The general formula for this process is $(a\sqrt[n]{x}) \cdot (b\sqrt[n]{y}) = (ab)\sqrt[n]{xy}$, which shows how to multiply the coefficients and the radicands.
05:52:13
AI Öğretmen
For example, if you want to multiply $2\sqrt{6}$ by $3\sqrt{3}$, start by multiplying the coefficients: $2 \times 3 = 6$.
05:52:15
AI Öğretmen
Then, multiply the radicands: $6 \times 3 = 18$. So, you have $6\sqrt{18}$.
05:52:16
AI Öğretmen
Next, you simplify $6\sqrt{18}$ by breaking $18$ into $9 \times 2$, because $9$ is a perfect square.
05:52:17
AI Öğretmen
The square root of $9$ is $3$, so $6\sqrt{9 \cdot 2}$ becomes $6 \times 3\sqrt{2}$.
05:52:19
AI Öğretmen
Finally, $6 \times 3 = 18$, so your answer is $18\sqrt{2}$.
05:52:19
AI Öğretmen
Did you understand how to multiply radicals and simplify the result?
05:53:29
Öğrenci
I got it
05:53:31
💭 AI Öğretmen
Let us review carefully
05:53:32
❓ Soru basic
Multiply $\sqrt{x}(4 - 3\sqrt{x})$
05:57:32
Öğrenci
My answer is in the attached image.
05:57:33
💭 AI Öğretmen
Let me review that carefully
05:57:44
AI Öğretmen
Fantastic job! You've correctly applied the distributive property to multiply the expression.
05:57:46
AI Öğretmen
You did great by multiplying $\sqrt{x}$ by both $4$ and $3\sqrt{x}$, and then correctly simplifying $\sqrt{x} \cdot \sqrt{x}$ to $x$.
05:57:47
AI Öğretmen
This shows a strong understanding of how to work with square roots and the distributive property!
05:57:48
AI Öğretmen
The correct answer is $4\sqrt{x} - 3x$.
05:57:48
AI Öğretmen
Should we continue with the lecture?
05:59:15
Öğrenci
Alright, let's continue
05:59:16
💭 AI Öğretmen
Preparing the next part
05:59:22
🎥 Video
05:59:22
AI Öğretmen
Did you understand how to apply the Quotient Rule for dividing radicals?
06:00:50
Öğrenci
I got it
06:00:52
💭 AI Öğretmen
Let us review this question
06:00:52
❓ Soru medium
Find the simplest form of the expression $\sqrt[3]{\frac{16x^8y^3}{250x^2z^6}}$, assuming that $x, y, \text{ and } z$ are positive real numbers.

Voltran Okul Analiz Sistemi