← Ana Rapor / Yusuf Ali KARAGÖL / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:29
Bitiş
Devam ediyor
Süre
11 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, ders boyunca genel olarak başarılı bir performans sergilemiştir. Sorulan soruların çoğuna doğru ve mantıklı açıklamalarla cevap vermiştir. Özellikle, bir fonksiyonun tanım kümesi (domain), değer kümesi (codomain) ve görüntü kümesini (range) doğru bir şekilde belirleme konusunda yetkin olduğu görülmektedir. Ayrıca, rasyonel bir fonksiyonun tanım kümesindeki kısıtlamaları (paydanın sıfır olmaması) doğru bir şekilde tespit edebilmiştir.

Ancak, öğrencinin bir fonksiyonun temel tanımında önemli bir noktayı tam olarak kavrayamadığı gözlemlenmiştir.

Öğrencinin Gelişim Alanları (Gaps)

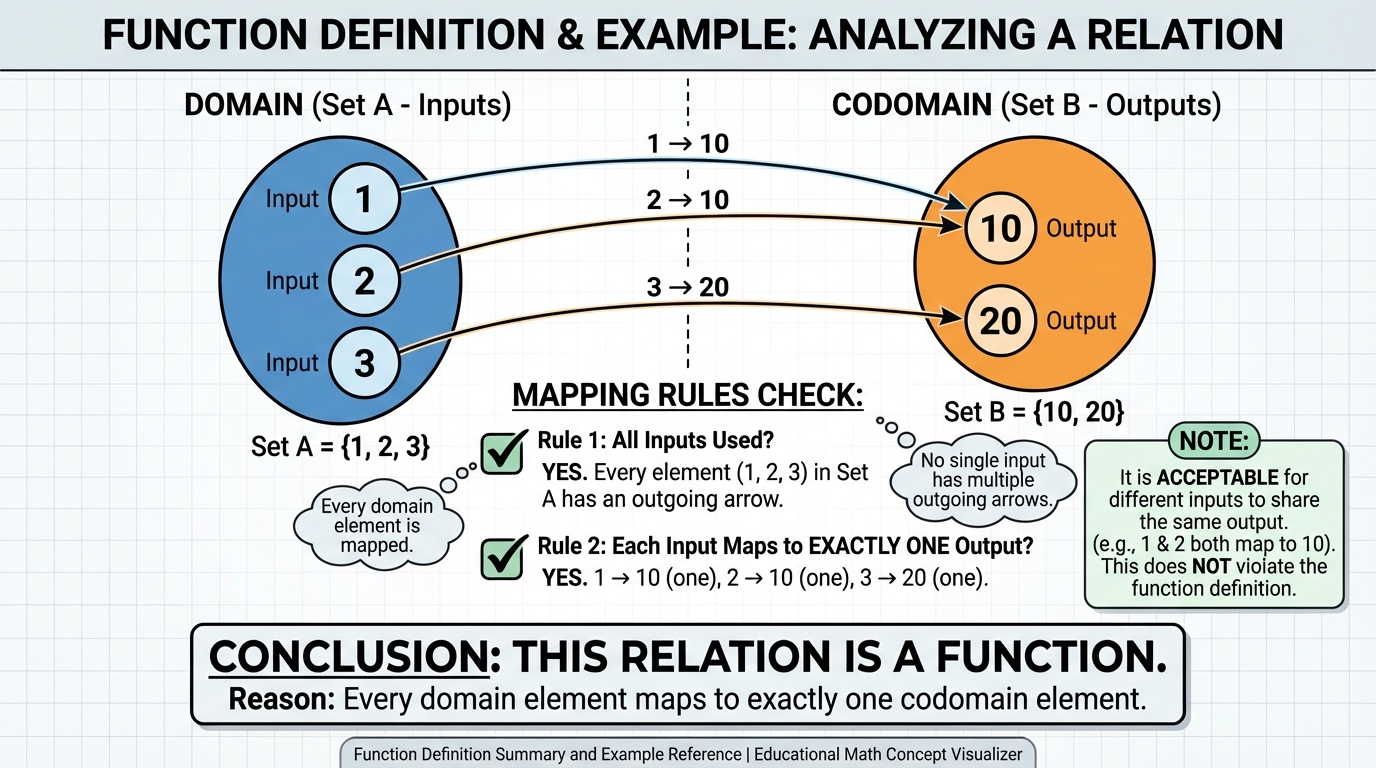
Öğrencinin en belirgin eksikliği, "farklı girdilerin neden aynı çıktıya sahip olabileceği" konusundaki kafa karışıklığıdır. `06:38:13`'te sorduğu "Why can different inputs share the same output in a function?" sorusu, fonksiyon tanımının temel bir kuralını (many-to-one ilişkisine izin verilmesi) tam olarak içselleştiremediğini göstermektedir. Bu, bir ilişkinin ne zaman fonksiyon olarak kabul edileceğine dair temel bir kavramsal boşluk olduğunu işaret etmektedir. Yapay zeka öğretmenin açıklamasından sonra konuyu anladığını belirtse de, bu soruyu sormuş olması bu konunun pekiştirilmesi gerektiğini göstermektedir.

Öğrencinin Başarılı Olduğu Alanlar

Öğrenci, aşağıdaki konularda başarılı bir anlayış sergilemiştir:

* Tanım, Değer ve Görüntü Kümesi: Verilen bir eşleme şemasından tanım, değer ve görüntü kümelerini hatasız bir şekilde çıkarmıştır (`06:33:10`).
* Fonksiyon Olma Şartının Uygulanması: Bir ifadenin (f(x) = x - 3) neden N'den N'ye bir fonksiyon olmadığını, çıktıların değer kümesinin dışına (negatif sayılar) taştığını doğru bir şekilde açıklamıştır (`06:36:21`).
* Tanım Kümesini Belirleme: Rasyonel bir ifadenin tanım kümesini, paydayı sıfır yapan değeri dışarıda bırakarak doğru şekilde bulmuştur (`06:40:15`).

Ders Dışı Yorumlar

Öğrencinin ders dışı herhangi bir sorusu veya yorumu olmamıştır.

📜 Oturum Detayları

06:30:23
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:30:25
💭 AI Öğretmen
Great, getting started now
06:30:25
🎥 Video
06:30:26
AI Öğretmen
Did you understand how a function connects elements from Set A to Set B?
06:31:02
Öğrenci
I got it
06:31:04
💭 AI Öğretmen
Let us proceed then
06:31:04
🎥 Video
06:31:05
AI Öğretmen
Do you feel clear about the differences between domain, codomain, and range?
06:31:42
Öğrenci
I got it
06:31:44
💭 AI Öğretmen
Let us proceed then
06:31:44
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:33:10
Öğrenci
My answer is: Domain: -1, 0, 1, 2 Codomain: 0, 1, 2, 3, 4, 5 Range: 0, 1, 4
06:33:10
💭 AI Öğretmen
Reviewing your answer now
06:33:15
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range from the function's mapping diagram.
06:33:16
AI Öğretmen
You clearly understand that the domain consists of all the input values, the codomain is the entire set of possible output values, and the range is the specific set of actual output values that the function produces.
06:33:18
AI Öğretmen
This shows a great grasp of how functions map elements from one set to another! Keep up the excellent work!
06:33:19
AI Öğretmen
Therefore the correct answer is Domain: $\{-1, 0, 1, 2\}$, Codomain: $\{0, 1, 2, 3, 4, 5\}$, Range: $\{0, 1, 4\}$
06:33:19
AI Öğretmen
Should we continue with the lecture?
06:33:57
Öğrenci
Alright, let's continue
06:33:58
💭 AI Öğretmen
Proceeding with lesson
06:34:07
Görsel
Görsel
06:34:10
AI Öğretmen
A relation is considered a function if it meets a specific rule.
06:34:11
AI Öğretmen
Every input, which means every element from the domain or set A, must be paired with one output in the codomain or set B.
06:34:13
AI Öğretmen
It is important to remember that not every element of set B needs to have a pair, so there can be unused elements in the codomain.
06:34:14
AI Öğretmen
It is also allowed for several inputs to share the same output, which means many-to-one connections are fine.
06:34:15
AI Öğretmen
However, a single input cannot be connected to more than one output; this one-to-many pattern is not allowed in a function.
06:34:17
AI Öğretmen
So, a function is a relation that links every domain element to exactly one value in the codomain.
06:34:18
AI Öğretmen
Did this explanation make the concept of functions clear to you?
06:34:57
Öğrenci
I got it
06:34:59
💭 AI Öğretmen
Now let's review this question
06:35:00
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:36:21
Öğrenci
My answer is: It is not a function from N to N because for natural numbers like 1 or 2, f(x) = x – 3 gives negative values which are not in N.
06:36:22
💭 AI Öğretmen
Let me review that carefully
06:36:26
AI Öğretmen
That's absolutely right! You've nailed it!
06:36:28
AI Öğretmen
You correctly identified that for a relation to be a function from $\mathbb{N}$ to $\mathbb{N}$, every natural number input must produce a natural number output.
06:36:29
AI Öğretmen
Your explanation clearly shows that values like 1 or 2 from the domain $\mathbb{N}$ result in negative numbers, which are not part of the codomain $\mathbb{N}$.
06:36:30
AI Öğretmen
This demonstrates a great understanding of what defines a function and how to check its domain and codomain!
06:36:30
AI Öğretmen
Should we continue with the lecture?
06:37:01
Öğrenci
Alright, let's continue
06:37:02
💭 AI Öğretmen
Moving ahead now
06:37:09
Görsel
Görsel
06:37:11
AI Öğretmen
A relation between two sets can be analyzed to determine if it is a function by checking specific rules.
06:37:12
AI Öğretmen
Let's look at two sets: Set A, which contains the inputs $\{1, 2, 3\}$, and Set B, which contains the outputs $\{10, 20\}$.
06:37:14
AI Öğretmen
In this example, the mapping is as follows: $1$ maps to $10$, $2$ maps to $10$, and $3$ maps to $20$.
06:37:14
AI Öğretmen
This means every input from Set A is matched to an output in Set B, and each input has only one output.
06:37:16
AI Öğretmen
It is allowed for different inputs to share the same output, like $1$ and $2$ both mapping to $10$.
06:37:17
AI Öğretmen
Therefore, this relation is a function because every element in the domain (inputs) is paired with exactly one element in the codomain (outputs).
06:37:18
AI Öğretmen
Did you understand how we determined that this relation is a function?
06:38:13
Öğrenci
Why can different inputs share the same output in a function?
06:38:15
💭 AI Öğretmen
Interesting thought process
06:38:19
AI Öğretmen
Different inputs can share the same output in a function because the rule only requires that each input has exactly one output, not that outputs must be unique.
06:38:20
AI Öğretmen
This means multiple inputs can map to the same output value, but no input can map to more than one output.
06:38:21
AI Öğretmen
For example, both 1 and 2 mapping to 10 is allowed, but one input mapping to two different outputs is not.
06:38:22
AI Öğretmen
Does this explanation make sense to you?
06:38:52
Öğrenci
I got it
06:38:54
💭 AI Öğretmen
Let's reinforce this concept
06:38:55
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:40:15
Öğrenci
My answer is: All real numbers except x = –2
06:40:16
💭 AI Öğretmen
Let me review that answer
06:40:20
AI Öğretmen
That's absolutely right! Fantastic job!
06:40:23
AI Öğretmen
You correctly identified that the denominator of a fraction cannot be zero, which is the key restriction for rational functions like this one.
06:40:25
AI Öğretmen
Remember, avoiding division by zero is crucial when determining the domain of any rational function. Keep up the great work!
06:40:26
AI Öğretmen
Therefore, the correct answer is All real numbers except x = –2.
06:40:26
AI Öğretmen
Should we continue with the lecture?
06:40:48
Öğrenci
Alright, let's continue
06:40:48
💭 AI Öğretmen
Moving to the next part
06:41:00
AI Öğretmen
A relation is considered a function when every input value from the domain is paired with only one output value in the codomain.
06:41:02
AI Öğretmen
It is acceptable for different inputs to share the same output, meaning multiple inputs can map to the same output.
06:41:03
AI Öğretmen
The important rule is that a single input cannot be matched with more than one output in a function.
06:41:04
AI Öğretmen
This is how we distinguish functions from general relations.
06:41:05
AI Öğretmen
Did you understand how to determine if a relation is a function based on the inputs and outputs?

Voltran Okul Analiz Sistemi