← Ana Rapor / Ela ENGÜR / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:45
Bitiş
Devam ediyor
Süre
13 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, dersin başında konunun detaylı bir şekilde anlatılmasını isteyerek derse ilgili ve öğrenmeye açık bir başlangıç yaptı. Ders boyunca, fonksiyonun artan ve azalan aralıklarını bir grafik üzerinden belirleme konusunda tam bir yetkinlik gösterdi.

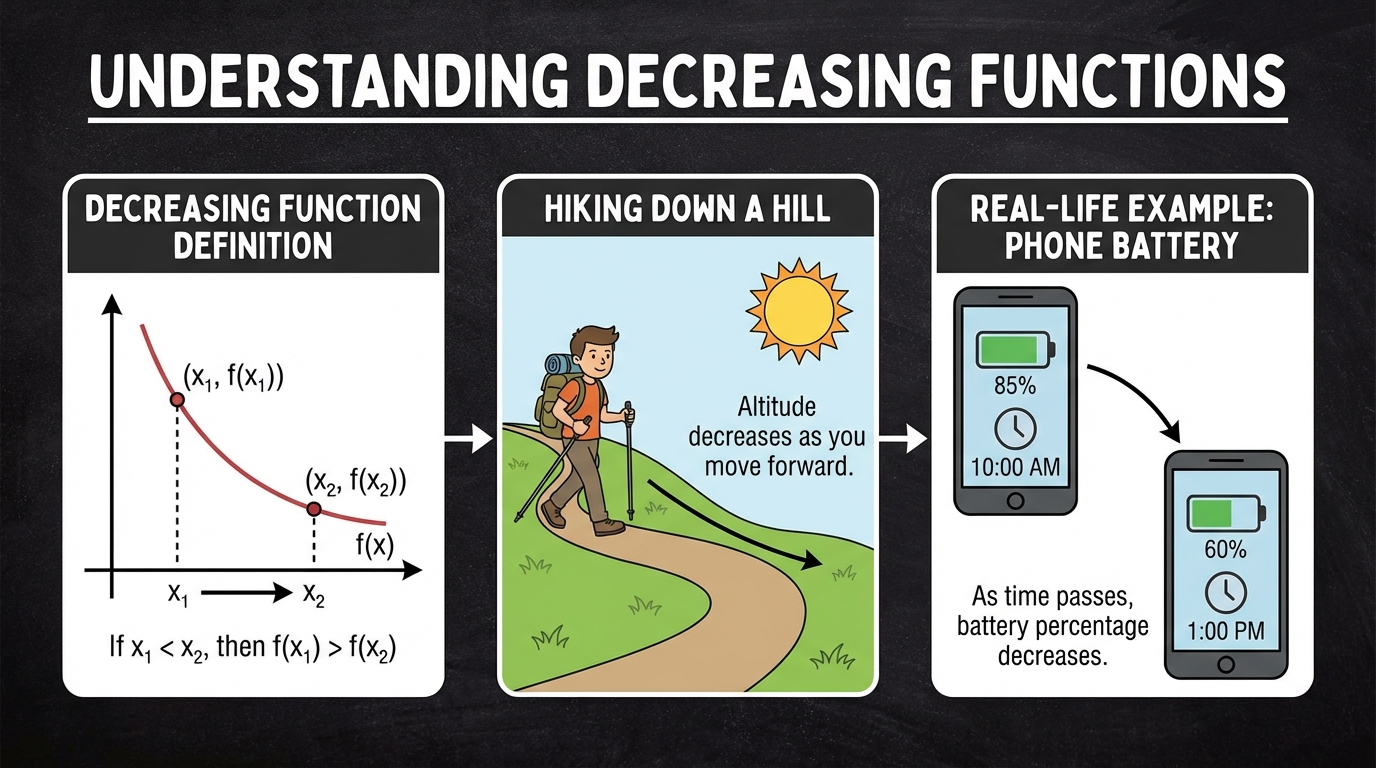
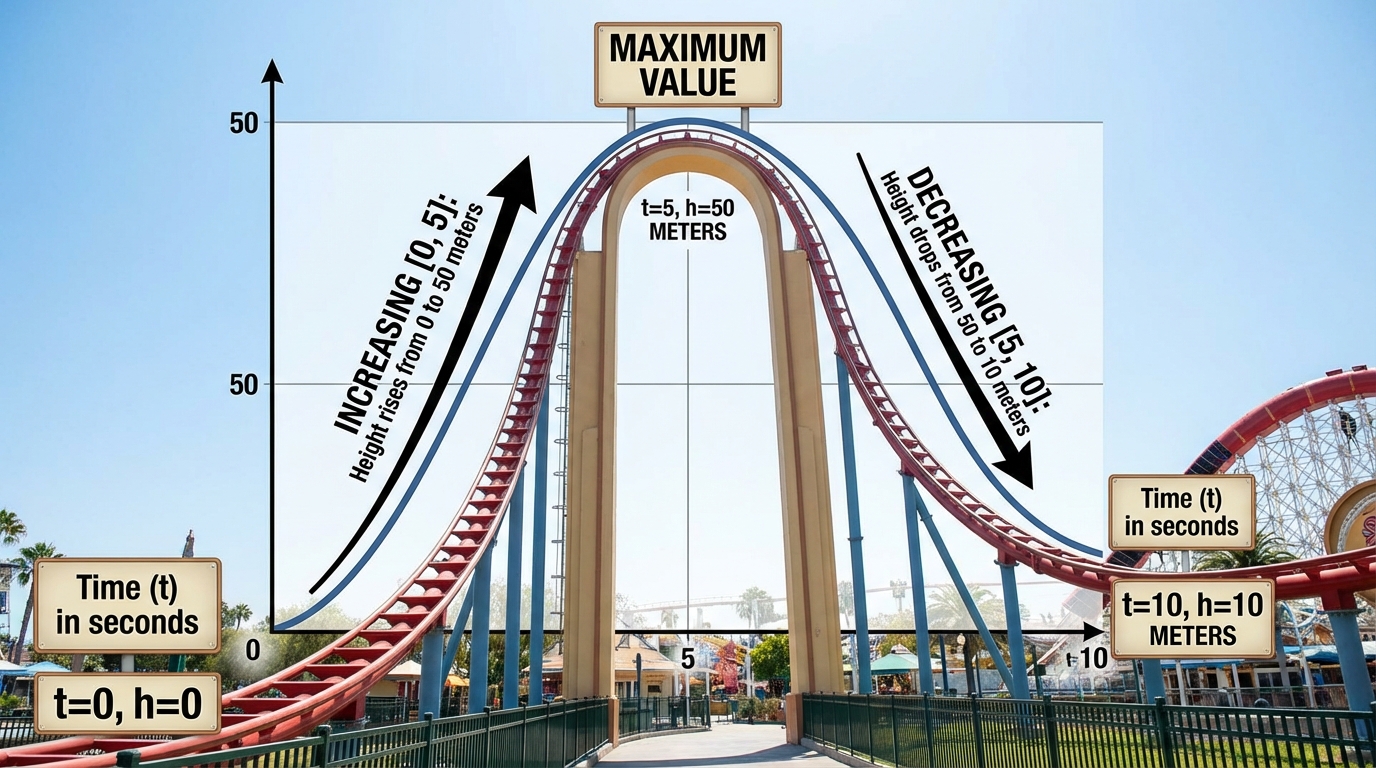
- Artan ve Azalan Aralıklar: Öğrenci, bir fonksiyonun grafiğine bakarak artan ve azalan olduğu aralıkları doğru bir şekilde tespit etti. Sorulan sorulara verdiği cevaplar (`[-5,-2] U [0,3]` ve `[-2,0]`) tamamen doğruydu.
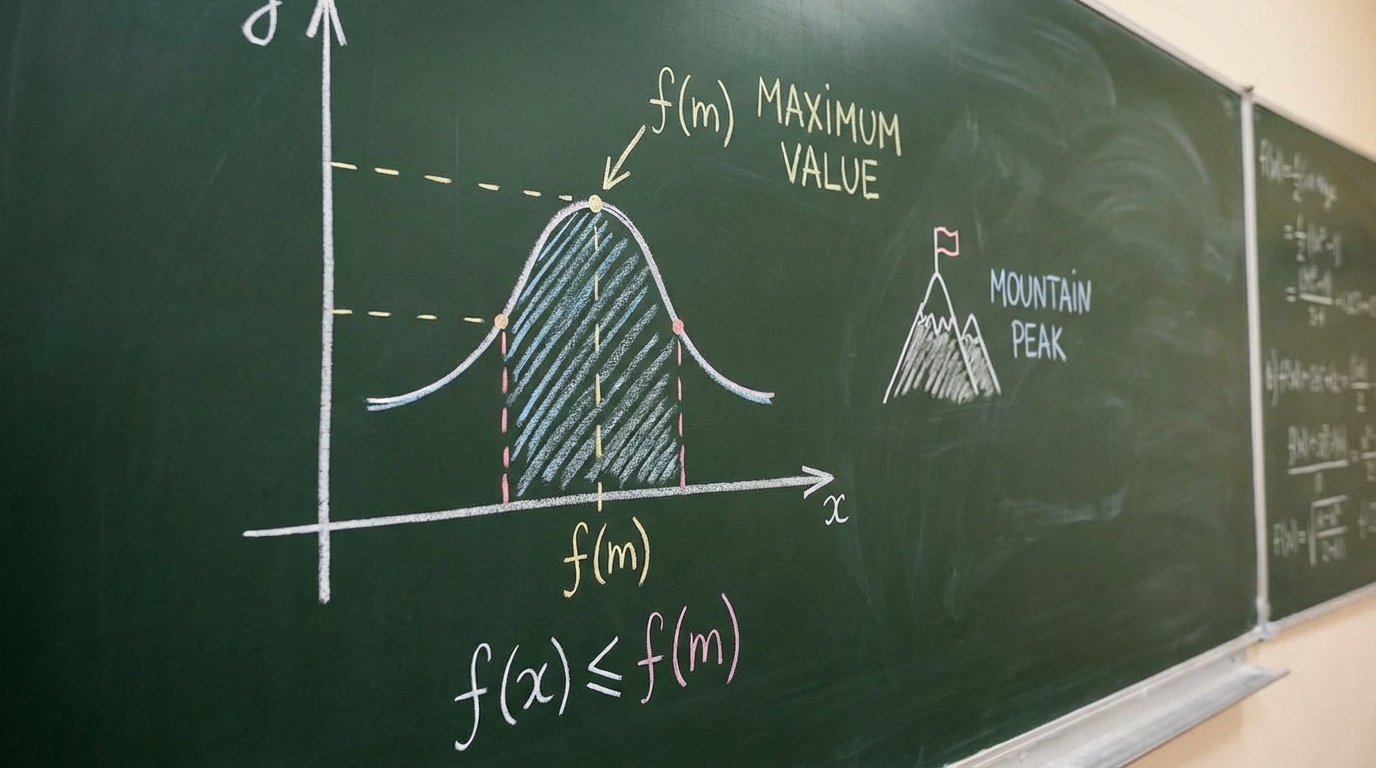
- Maksimum Değer: Fonksiyonun maksimum değerini (grafikteki en yüksek tepe noktasını) bulma konusunda da başarılı oldu ve sorulan tüm soruları doğru yanıtladı.
- Anlama Seviyesi: Her açıklama sonrasında "Anladım" ("I got it") diyerek geri bildirimde bulundu ve bu anlayışını sorduğu sorulara verdiği doğru cevaplarla kanıtladı. Herhangi bir ek ipucuna veya tekrar açıklamaya ihtiyaç duymadı.

Genel olarak, öğrencinin bu derste işlenen "Bir Fonksiyonun Artan ve Azalan Aralıkları" konusunu mükemmel bir şekilde anladığı ve uygulamaya geçirebildiği görülmektedir.

Konu Analizi

📜 Oturum Detayları

06:46:38
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:46:39
💭 AI Öğretmen
Great, getting the details ready
06:46:39
Görsel
Görsel
06:46:41
AI Öğretmen
Graphs in mathematics are always read from left to right, just like reading a sentence in English.
06:46:42
AI Öğretmen
This point of view is important for understanding how a function behaves as you move along its graph.
06:46:44
AI Öğretmen
When we look at two different $x$-values, we always look from the one on the left to the one on the right.
06:46:47
AI Öğretmen
We check to see if the function goes up or down between these two $x$-values by following this left-to-right direction.
06:46:48
AI Öğretmen
Remembering to read the graph from left to right will help you know exactly where a function is increasing or decreasing.
06:46:49
AI Öğretmen
Did you understand how we use the left-to-right direction to determine if a function is increasing or decreasing?
06:47:38
Öğrenci
I got it
06:47:41
💭 AI Öğretmen
Let us continue
06:47:42
🎥 Video
06:47:42
AI Öğretmen
Did you understand how increasing intervals work in a function?
06:48:52
Öğrenci
I got it
06:48:55
💭 AI Öğretmen
Let us proceed shortly
06:48:55
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_33e16c0c-dc3a-47bd-91c9-e1d47eecd95c.png) Example: The graph of f is shown on the below. Find the intervals of x for which f(x) is **increasing**.
06:50:27
Öğrenci
My answer is: [-5,-2] U [0,3]
06:50:27
💭 AI Öğretmen
Noted your answer
06:50:32
AI Öğretmen
That's absolutely right! Fantastic job!
06:50:32
AI Öğretmen
You correctly identified that a function is increasing when its graph goes upwards as you move from left to right.
06:50:33
AI Öğretmen
You clearly understood how to find the intervals where the y-values are rising with increasing x-values. Keep up the great work!
06:50:35
AI Öğretmen
Therefore, the correct answer is [-5, -2] U [0, 3].
06:50:35
AI Öğretmen
Should we continue with the lecture?
06:51:08
Öğrenci
Alright, let's continue
06:51:08
💭 AI Öğretmen
Preparing next part
06:51:15
Görsel
Görsel
06:51:18
AI Öğretmen
A function is called decreasing on an interval when, if you pick any two points $x_1$ and $x_2$ in that interval, and $x_1$ is less than $x_2$, then $f(x_1)$ is greater than $f(x_2)$.
06:51:19
AI Öğretmen
This means that as you move to the right along the $x$-axis, the value of the function goes down.
06:51:21
AI Öğretmen
Think about walking down a hill—every step forward takes you lower in height, just like the function's value is getting smaller.
06:51:23
AI Öğretmen
An example you see every day is your phone’s battery going down over time, showing how its percentage drops as the hours pass, which is just like a decreasing function.
06:51:24
AI Öğretmen
Did this explanation about decreasing functions make sense to you?
06:52:09
Öğrenci
I got it
06:52:11
💭 AI Öğretmen
Let us proceed now
06:52:11
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_fb69fa74-e294-4d91-a021-e549025bd3c4.png) Example: The graph of $f$ is shown on the above. Find the intervals of $x$ for which $f(x)$ is **decreasing**.
06:54:01
Öğrenci
My answer is: [-2,0]
06:54:02
💭 AI Öğretmen
Let me review your answer
06:54:07
AI Öğretmen
That's absolutely correct! Fantastic job!
06:54:08
AI Öğretmen
You correctly identified that the function is decreasing in the interval [-2, 0].
06:54:10
AI Öğretmen
This shows you understand that a function is decreasing when its graph moves downwards as you look from left to right.
06:54:10
AI Öğretmen
Keep up the great work!
06:54:11
AI Öğretmen
Therefore the correct answer is [-2, 0].
06:54:11
AI Öğretmen
Should we continue with the lecture?
06:54:31
Öğrenci
Alright, let's continue
06:54:32
💭 AI Öğretmen
Moving on to decreasing functions
06:54:39
Görsel
Görsel
06:54:41
AI Öğretmen
The maximum value of a function is the highest output that the function reaches in a certain interval.
06:54:42
AI Öğretmen
Mathematically, we say that $f(m)$ is the maximum if, for every $x$ in the interval, $f(x) \leq f(m)$.
06:54:43
AI Öğretmen
This definition is about the absolute highest value that the function achieves in that interval.
06:54:44
AI Öğretmen
On a graph, the maximum can be seen as the very top or "peak" point, where the function stops going up and starts going down.
06:54:46
AI Öğretmen
Not every function has a maximum value in every interval, but if there is one, it looks like the top of a mountain on the graph.
06:54:46
AI Öğretmen
Did you understand how the maximum value of a function is identified within an interval?
06:55:32
Öğrenci
I got it
06:55:35
💭 AI Öğretmen
Let's prepare for the question
06:55:35
❓ Soru basic
**Example:** The graph of $g$ is shown below. Find the intervals of $x$ for which $g(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?** ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_11a805a3-b66d-431d-99b4-450c738ea61d.png)
06:56:32
Öğrenci
My answer is: Max=3
06:56:33
💭 AI Öğretmen
Noted your answer
06:56:37
AI Öğretmen
Fantastic job! You've correctly identified the maximum value of the function.
06:56:38
AI Öğretmen
The maximum value is indeed 3 because that's the highest point the graph reaches on the y-axis.
06:56:39
AI Öğretmen
Remember, the maximum value of a function is the greatest y-value it attains, representing its peak.
06:56:40
AI Öğretmen
Keep up the great work!
06:56:41
AI Öğretmen
Therefore, the correct answer is 3.
06:56:41
AI Öğretmen
Should we continue with the lecture?
06:57:06
Öğrenci
Alright, let's continue
06:57:07
💭 AI Öğretmen
Continuing with the next concept
06:57:14
Görsel
Görsel
06:57:18
AI Öğretmen
Think of a rollercoaster example, where t stands for time and h stands for height.
06:57:19
AI Öğretmen
In this case, the function we are looking at tells us the rollercoaster's height at each moment in time.
06:57:21
AI Öğretmen
The function is said to be increasing on the interval from 0 to 5 seconds, written as $[0,5]$, because the height goes up from 0 meters to 50 meters while time increases from 0 to 5 seconds.
06:57:22
AI Öğretmen
At $t=5$ seconds, the rollercoaster reaches its highest point, which is 50 meters.
06:57:23
AI Öğretmen
After that, the function is decreasing on the interval from 5 to 10 seconds, noted as $[5,10]$, since the height falls from 50 meters to 10 meters between those times.
06:57:25
AI Öğretmen
Writing intervals like $[0,5]$ and $[5,10]$ makes it clear where the function, or the rollercoaster’s height, is increasing or decreasing over time.
06:57:26
AI Öğretmen
Did you understand how the function describes the rollercoaster's height changes over time?
06:58:14
Öğrenci
I got it
06:58:16
💭 AI Öğretmen
Let us review carefully
06:58:17
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_5a453885-672f-4b3c-b466-4fe71a09d85a.png) **Example:** The graph of $f$ is shown above. Find the intervals of $x$ for which $f(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?**
06:59:12
Öğrenci
My answer is: max=2
06:59:13
💭 AI Öğretmen
Let me process that
06:59:16
AI Öğretmen
Fantastic job! You are absolutely correct!
06:59:17
AI Öğretmen
The maximum value of a function is indeed the highest y-coordinate that the function reaches on its graph.
06:59:19
AI Öğretmen
You correctly identified that the highest point on this graph is where y equals 2, which shows you have a great understanding of how to read function values from a graph.
06:59:19
AI Öğretmen
Keep up the excellent work!
06:59:20
AI Öğretmen
Therefore the correct answer is max=2
06:59:20
AI Öğretmen
Should we continue with the lecture?
06:59:50
Öğrenci
Alright, let's continue
06:59:51
💭 AI Öğretmen
Preparing next explanation
07:00:00
AI Öğretmen
In this lesson, we covered how to read graphs from left to right to understand function behavior, defined increasing and decreasing intervals using real-life examples, and learned how to identify the maximum value of a function within an interval. Do you have any questions about these topics? If not, we can wrap up the lesson here.

Voltran Okul Analiz Sistemi