← Ana Rapor / Ali ARAS / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:28
Bitiş
Devam ediyor
Süre
13 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
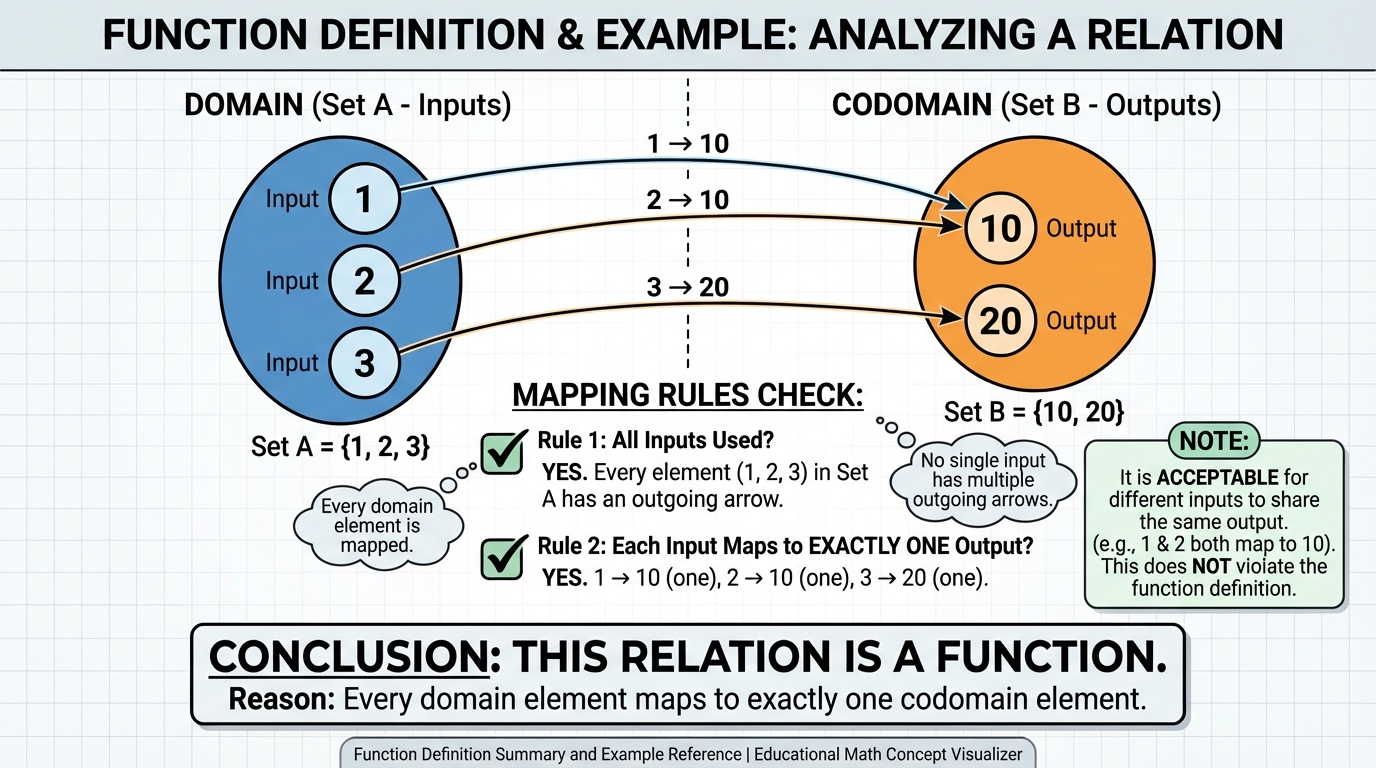
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Öğrenci Performans Analizi

# Genel Değerlendirme
Öğrenci ders boyunca konuya ilgili ve katılımcı bir tutum sergilemiştir. Fonksiyonların temel bileşenleri (tanım kümesi, değer kümesi, görüntü kümesi) ve fonksiyon değeri hesaplama gibi pratik konularda başarılı bir performans göstermiştir. Ancak, bir bağıntının "fonksiyon" olarak tanımlanabilmesi için gereken en temel ve kritik kuralı (tanım kümesindeki her elemanın değer kümesinde bir karşılığı olması zorunluluğu) tam olarak kavrayamadığı görülmüştür. Bu teorik eksiklik, öğrencinin fonksiyon tanımını daha derinlemesine anlaması gerektiğini göstermektedir.

# İyi Olduğu Konular
Öğrenci, aşağıdaki becerileri başarıyla sergilemiştir:
* Tanım, Değer ve Görüntü Kümesini Belirleme: Verilen bir şematik gösterimde bir fonksiyonun tanım kümesini, değer kümesini ve görüntü kümesini doğru bir şekilde tespit etmiştir.
* Rasyonel Fonksiyonlarda Tanım Kümesi Bulma: Paydayı sıfır yapan değeri bularak bir rasyonel fonksiyonun en geniş tanım kümesini doğru bir şekilde belirlemiştir.
* Fonksiyon Değeri Hesaplama: `f(x-1)` gibi dolaylı olarak verilmiş bir fonksiyonda istenen `f(3)` değerini, doğru değişken dönüşümünü yaparak başarıyla hesaplamıştır.

# Eksik Olduğu Konular
Öğrencinin en belirgin eksiği, fonksiyon olmanın temel tanımını ve şartlarını anlamada ortaya çıkmıştır:
* Fonksiyon Olma Şartları: "f(x) = x - 3 bağıntısı N'den N'ye bir fonksiyon mudur?" sorusuna "Evet" cevabını vermiştir. Bu cevap, öğrencinin tanım kümesindeki her elemanın (örneğin x=1 veya x=2 için) sonucunun değer kümesinde (Doğal Sayılar - N) olması gerektiği kuralını gözden kaçırdığını göstermektedir. Bu, fonksiyonun en temel tanımına dair bir kavram yanılgısıdır.

# Tamamen Ders Dışı Sorular/Yorumlar
Ders dışı herhangi bir yorum veya soru kaydedilmemiştir.

📜 Oturum Detayları

06:28:35
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:28:37
💭 AI Öğretmen
Great, getting started now
06:28:37
🎥 Video
06:28:37
AI Öğretmen
Did you understand how a function relates elements from Set A to Set B?
06:29:14
Öğrenci
I got it
06:29:17
💭 AI Öğretmen
Let us continue now
06:29:18
🎥 Video
06:29:19
AI Öğretmen
Did you understand how the domain, codomain, and range relate to each other in a function?
06:30:02
Öğrenci
I got it
06:30:04
💭 AI Öğretmen
Let us proceed carefully
06:30:05
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:31:09
Öğrenci
My answer is: Domaine : -1, 0, 1, 2 CoDomain : 0, 1, 2, 3, 4, 5 Range: 0, 1 ,4
06:31:10
💭 AI Öğretmen
Reviewing your response now
06:31:14
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range for the function.
06:31:16
AI Öğretmen
You clearly understand that the domain is all possible inputs, the codomain is all possible outputs, and the range is the set of actual outputs that the function maps to.
06:31:18
AI Öğretmen
Keep up the great work!
06:31:21
AI Öğretmen
Therefore the correct answer is Domain: $\{-1, 0, 1, 2\}$, Codomain: $\{0, 1, 2, 3, 4, 5\}$, Range: $\{0, 1, 4\}$
06:31:21
AI Öğretmen
Should we continue with the lecture?
06:31:57
Öğrenci
Alright, let's continue
06:31:58
💭 AI Öğretmen
Proceeding to next step
06:32:04
Görsel
Görsel
06:32:07
AI Öğretmen
A relation is called a function if it follows an important rule.
06:32:10
AI Öğretmen
Every input, which means every element from the domain (sometimes called Set A), must be connected to some output in the codomain (Set B).
06:32:12
AI Öğretmen
This does not mean that every value in the codomain needs to be used—some elements in Set B might not be matched with anything from Set A, and that's perfectly fine.
06:32:14
AI Öğretmen
It is allowed for different inputs, or elements from Set A, to share the same output in Set B, which is known as a many-to-one mapping.
06:32:17
AI Öğretmen
However, one input cannot be paired with more than one output—this is called one-to-many, and it is not allowed for a function.
06:32:19
AI Öğretmen
So, to summarize, a function matches every element of the domain to exactly one element in the codomain, making sure each input has only one output.
06:32:20
AI Öğretmen
Does this explanation about functions make sense to you?
06:33:11
Öğrenci
I got it
06:33:13
💭 AI Öğretmen
Let's reinforce this concept
06:33:14
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:33:38
Öğrenci
My answer is: yes
06:33:39
💭 AI Öğretmen
Noted, processing your input
06:33:45
AI Öğretmen
Your answer was not correct, let me explain why the relation \( f(x) = x - 3 \) is not a function from \(\mathbb{N}\) to \(\mathbb{N}\).
06:33:46
AI Öğretmen
A function must assign every input in the domain to an output in the codomain, but here, when you plug in small natural numbers like \( x = 1 \), the output \( f(1) = 1 - 3 = -2 \), which is not a natural number.
06:33:50
AI Öğretmen
Since \(-2\) is not in the codomain \(\mathbb{N}\), the relation does not give a valid output for every input in the domain, so it fails the definition of a function from \(\mathbb{N}\) to \(\mathbb{N}\).
06:33:51
AI Öğretmen
A common misconception is thinking that any formula defines a function without checking if the outputs stay within the codomain. For example, \( f(x) = x + 1 \) is a function from \(\mathbb{N}\) to \(\mathbb{N}\) because the output is always a natural number.
06:33:53
AI Öğretmen
Therefore, the correct answer should be: No, it is not a function.
06:33:53
AI Öğretmen
Should we continue with the lecture?
06:34:53
Öğrenci
Alright, let's continue
06:34:54
💭 AI Öğretmen
Continuing with the lecture
06:34:58
Görsel
Görsel
06:35:01
AI Öğretmen
A relation between two sets can be checked to see if it is a function by following certain rules.
06:35:02
AI Öğretmen
Let's take two sets: Set A, which is the inputs $\{1, 2, 3\}$, and Set B, which is the outputs $\{10, 20\}$.
06:35:03
AI Öğretmen
The mapping between these sets is given as: $1 \to 10$, $2 \to 10$, $3 \to 20$.
06:35:04
AI Öğretmen
This means input 1 is paired with 10, input 2 is also paired with 10, and input 3 is paired with 20.
06:35:05
AI Öğretmen
Each input from Set A is used, and each one points to only one output in Set B.
06:35:08
AI Öğretmen
It's okay if different inputs lead to the same output, like 1 and 2 both pointing to 10.
06:35:09
AI Öğretmen
The conclusion is that this relation is a function because every element from the domain has exactly one match in the codomain.
06:35:10
AI Öğretmen
Did you understand why this relation qualifies as a function?
06:36:07
Öğrenci
I got it
06:36:10
💭 AI Öğretmen
Let us review this example
06:36:10
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:37:27
Öğrenci
My answer is: R-(-2)
06:37:29
💭 AI Öğretmen
Let me review that answer
06:37:33
AI Öğretmen
That's absolutely right! Fantastic job!
06:37:35
AI Öğretmen
You correctly identified that the denominator of a fraction cannot be zero, which is the key restriction for rational functions like this one.
06:37:35
AI Öğretmen
Understanding how to find the domain by excluding values that make the denominator zero is a crucial skill in algebra. Keep up the great work!
06:37:36
AI Öğretmen
Therefore, the correct answer is R-(-2).
06:37:36
AI Öğretmen
Should we continue with the lecture?
06:38:08
Öğrenci
Alright, let's continue
06:38:09
💭 AI Öğretmen
Moving forward now
06:38:17
AI Öğretmen
A relation can be called a function only if every input value in the domain matches to one and only one output value in the codomain.
06:38:18
AI Öğretmen
This means each input must connect to exactly one output, not more than one.
06:38:19
AI Öğretmen
It's okay for different inputs to have the same output, but one input cannot have more than one output.
06:38:20
AI Öğretmen
Do you feel clear about how to identify a function based on its inputs and outputs?
06:40:09
Öğrenci
I got it
06:40:11
💭 AI Öğretmen
Let us proceed with the question
06:40:11
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:40:41
Öğrenci
My answer is: 18
06:40:42
💭 AI Öğretmen
Let me review that answer
06:40:46
AI Öğretmen
That's absolutely correct! Fantastic job!
06:40:48
AI Öğretmen
You correctly figured out that to find $f(3)$, you needed to set $x - 1 = 3$, which means $x$ must be $4$.
06:40:50
AI Öğretmen
Then, by substituting $x=4$ into $4x + 2$, you got $4(4) + 2 = 16 + 2 = 18$.
06:40:50
AI Öğretmen
This shows you have a great understanding of how to evaluate functions when the input is expressed in terms of another variable. Keep up the excellent work!
06:40:52
AI Öğretmen
Therefore, the correct answer is 18.
06:40:52
AI Öğretmen
Should we continue with the lecture?
06:41:33
Öğrenci
Alright, let's continue
06:41:34
💭 AI Öğretmen
Proceeding to next concept
06:41:42
AI Öğretmen
In this lesson, we covered the definition of a function as a relation where every input from the domain maps to exactly one output in the codomain. We also discussed the roles of domain, codomain, and range, and how to determine if a relation is a function by checking these rules. Finally, we looked at examples illustrating these concepts. Do you have any questions about these topics? If not, I'll end the lesson.

Voltran Okul Analiz Sistemi