← Ana Rapor / Giz Derin TAŞ / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:36
Bitiş
02 December 2025, 06:50
Süre
15 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Genel Değerlendirme
Öğrenci, fonksiyonların temel tanımları konusunda karma bir performans sergilemiştir. Tanım, değer ve görüntü kümesi gibi temel kavramları bir diyagram üzerinden doğru bir şekilde tespit edebilmekle birlikte, fonksiyon tanımının daha soyut ve cebirsel uygulamalarında zorluk yaşamıştır. Özellikle, bir ifadenin belirli bir tanım ve değer kümesi üzerinde fonksiyon olup olmadığını belirlerken ve girdi değeri değiştirilmiş bir fonksiyonun değerini bulurken yardıma ihtiyaç duymuş ve hata yapmıştır.

Başarılı Olduğu Noktalar
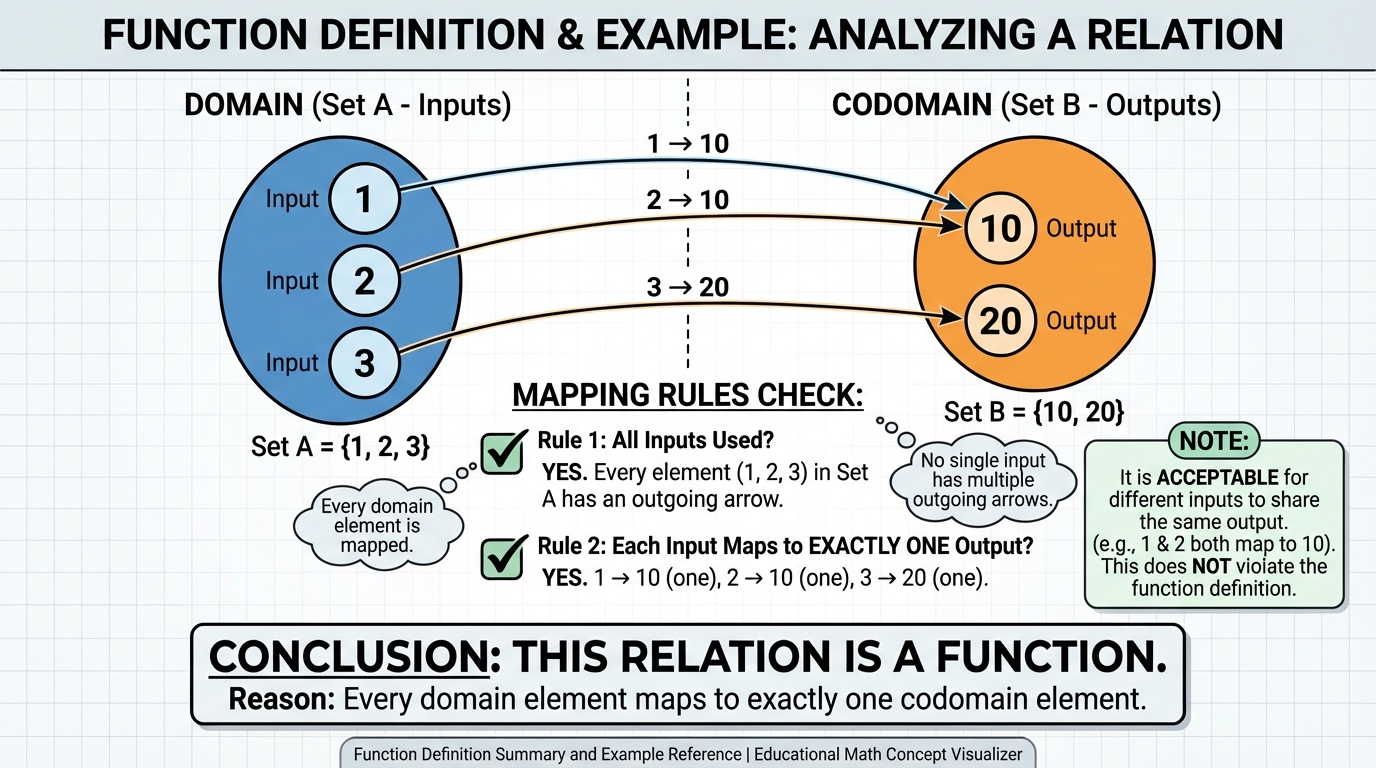
* Diyagramdan Fonksiyon Analizi: Öğrenci, bir VENN şeması ile gösterilen ilişkiden tanım, değer ve görüntü kümelerini doğru bir şekilde tespit etmiştir.
* Rasyonel Fonksiyonlarda Tanım Kümesi: Paydası olan bir rasyonel ifadenin en geniş tanım kümesini, paydayı sıfır yapan değeri dışarıda bırakarak doğru bir şekilde bulmuştur.

İyileştirilmesi Gereken Noktalar
* Fonksiyon Olma Şartının Uygulanması: Öğrenciye, tanım kümesi ve değer kümesi Doğal Sayılar (N) olan `f(x) = x - 3` ifadesinin bir fonksiyon olup olmadığı sorulduğunda, tanım kümesindeki bazı elemanların (1, 2 gibi) görüntüsünün değer kümesinde (N) yer almadığını fark edememiş ve cevabı bulmak için iki kez ipucu istemiştir. Bu durum, fonksiyon olma şartını (tanım kümesinde boşta eleman kalmaması) soyut durumlarda uygulamakta zorlandığını göstermektedir.
* Fonksiyon Notasyonu ve Değer Bulma: Dersteki en belirgin eksiklik, `f(x - 1) = 4x + 2` verilip `f(3)` değeri sorulduğunda yaşanmıştır. Öğrenci, `x - 1` ifadesini 3'e eşitleyip doğru `x` değerini bularak çözüme gitmek yerine, `x` yerine doğrudan 3 yazarak yanlış bir sonuca ulaşmıştır. Bu, fonksiyon notasyonunu ve bir fonksiyonun istenen bir noktadaki değerini bulma mantığını tam olarak kavramadığını göstermektedir. Bu soru için ipucu istemesine rağmen cevabı yanlış olmuştur.

📜 Oturum Detayları

06:36:06
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:36:07
💭 AI Öğretmen
Great, let us begin.
06:36:08
🎥 Video
06:36:08
AI Öğretmen
Did you understand how a function relates elements from one set to another?
06:36:43
Öğrenci
I got it
06:36:45
💭 AI Öğretmen
Let us continue now
06:36:46
🎥 Video
06:36:46
AI Öğretmen
Did you understand how the domain, codomain, and range relate to each other in a function?
06:37:24
Öğrenci
I got it
06:37:26
💭 AI Öğretmen
Let us move forward
06:37:26
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:38:22
Öğrenci
My answer is: Domain: {-1,0,1,2} Codomain: {0,1,2,3,4,5} Range: {0,1,4}
06:38:23
💭 AI Öğretmen
Reviewing your response
06:38:29
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range of the function from the diagram.
06:38:30
AI Öğretmen
Your answer shows a great understanding that the domain is all the input values, the codomain is the entire set of possible output values, and the range is the specific set of actual output values that the function produces.
06:38:32
AI Öğretmen
It's super important to distinguish between the codomain (all possibilities) and the range (what actually gets hit). Keep up the excellent work!
06:38:33
AI Öğretmen
Therefore, the correct answer is Domain: $\\{-1, 0, 1, 2\\}$, Codomain: $\\{0, 1, 2, 3, 4, 5\\}$, Range: $\\{0, 1, 4\\}$
06:38:33
AI Öğretmen
Should we continue with the lecture?
06:39:16
Öğrenci
Alright, let's continue
06:39:17
💭 AI Öğretmen
Proceeding to next step
06:39:22
Görsel
Görsel
06:39:26
AI Öğretmen
A relation is called a function if every input, which is an element from the domain (or Set A), is matched to some output in the codomain (Set B).
06:39:27
AI Öğretmen
This means that for each element in the domain, there is one and only one value that it is paired with in the codomain.
06:39:28
AI Öğretmen
However, not every element of the codomain (Set B) needs to be matched, so it's fine if there are some leftovers in the set of possible outputs.
06:39:31
AI Öğretmen
It is also acceptable for more than one input (from Set A) to be matched to the same output in Set B, allowing for many-to-one mappings.
06:39:34
AI Öğretmen
But it is not okay for one input to be matched to more than one output, which means a function cannot assign two or more different outputs to the same input.
06:39:35
AI Öğretmen
So, a function always assigns exactly one value in the codomain to each element of the domain.
06:39:37
AI Öğretmen
Did you understand how a relation qualifies as a function based on the input-output rules?
06:40:20
Öğrenci
I got it
06:40:23
💭 AI Öğretmen
Let us proceed carefully
06:40:23
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:40:50
Öğrenci
Can you give me a hint, teacher?
06:40:51
💭 AI Öğretmen
Let me review that first
06:40:55
AI Öğretmen
What does the domain $\mathbb{N}$ include, and what happens if you subtract 3 from some of its smallest elements?
06:40:57
AI Öğretmen
How does the definition of a function relate to whether the outputs after subtracting 3 still belong to the codomain $\mathbb{N}$?
06:40:58
AI Öğretmen
Can every input in the domain produce an output that is also a natural number under the rule $f(x) = x - 3$?
06:41:47
Öğrenci
Can you give me a hint, teacher?
06:41:48
💭 AI Öğretmen
Let me review that quickly
06:41:50
AI Öğretmen
What does the set of natural numbers $\mathbb{N}$ include, especially its smallest elements?
06:41:52
AI Öğretmen
If you subtract 3 from these smallest natural numbers, do you still get a natural number?
06:41:54
AI Öğretmen
How does this affect whether $f(x) = x - 3$ can be a function from $\mathbb{N}$ to $\mathbb{N}$?
06:42:35
Öğrenci
My answer is: not a function
06:42:36
💭 AI Öğretmen
Unfortunately.
06:42:40
AI Öğretmen
That's absolutely right! Fantastic job!
06:42:43
AI Öğretmen
You correctly identified that this relation is not a function because for some natural numbers in the domain, like 1 or 2, the output $f(x) = x - 3$ would result in a negative number.
06:42:44
AI Öğretmen
Since negative numbers are not part of the natural numbers (the codomain), not every element in the domain has a valid image, which is a key requirement for a function.
06:42:45
AI Öğretmen
Therefore, the correct answer is: not a function.
06:42:45
AI Öğretmen
Should we continue with the lecture?
06:43:12
Öğrenci
Alright, let's continue
06:43:13
💭 AI Öğretmen
Moving ahead now
06:43:18
Görsel
Görsel
06:43:21
AI Öğretmen
A relation links elements from one set, called the input set, to another set, called the output set.
06:43:22
AI Öğretmen
To tell if this relation is a function, we must check whether every input from Set A has one and only one output in Set B.
06:43:23
AI Öğretmen
Set A, which is our input set, has the elements 1, 2, and 3.
06:43:24
AI Öğretmen
Set B, the output set, has the elements 10 and 20.
06:43:27
AI Öğretmen
The way the relation works is that 1 goes to 10, 2 goes to 10, and 3 goes to 20.
06:43:29
AI Öğretmen
We can see that each input value from Set A is matched with one output value from Set B.
06:43:30
AI Öğretmen
None of the input numbers are left out, and none of the input numbers are matched with more than one output.
06:43:32
AI Öğretmen
It does not matter that more than one input can be matched with the same output. For example, both 1 and 2 are matched with 10, and that is allowed in a function.
06:43:34
AI Öğretmen
Because every input from Set A gets exactly one output from Set B, this relation is called a function.
06:43:35
AI Öğretmen
Did you understand why the given relation is considered a function?
06:44:23
Öğrenci
I got it
06:44:26
💭 AI Öğretmen
Let's reinforce this knowledge.
06:44:26
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:45:09
Öğrenci
My answer is: all real numbers except -2
06:45:10
💭 AI Öğretmen
That is an interesting response
06:45:15
AI Öğretmen
Fantastic job! You've absolutely nailed it!
06:45:16
AI Öğretmen
You correctly identified that for a rational function, the denominator cannot be zero, which means $x+2 \neq 0$.
06:45:17
AI Öğretmen
This shows you understand the crucial concept of avoiding division by zero when determining the domain of functions like this. Keep up the great work!
06:45:19
AI Öğretmen
Therefore, the correct answer is all real numbers except -2.
06:45:19
AI Öğretmen
Should we continue with the lecture?
06:45:44
Öğrenci
Alright, let's continue
06:45:45
💭 AI Öğretmen
Preparing the next part
06:45:53
AI Öğretmen
A relation is a function if every input value from the domain connects to only one output value in the codomain.
06:45:55
AI Öğretmen
This means that you cannot have one input matching with two or more different outputs.
06:45:56
AI Öğretmen
However, it is completely fine if different inputs connect to the same output.
06:45:58
AI Öğretmen
So, a function only needs each input to choose one output, but outputs can be shared by more than one input.
06:45:59
AI Öğretmen
Does the idea that each input must have exactly one output make sense to you?
06:46:24
Öğrenci
I got it
06:46:27
💭 AI Öğretmen
Let us review this carefully
06:46:28
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:46:52
Öğrenci
Can you give me a hint, teacher?
06:46:53
💭 AI Öğretmen
Let me review that quickly
06:46:56
AI Öğretmen
What does the expression \( f(x - 1) = 4x + 2 \) tell you about how to find \( f \) at a particular input?
06:46:57
AI Öğretmen
If you want to find \( f(3) \), how could you relate 3 to the expression \( x - 1 \) in the function definition?
06:46:58
AI Öğretmen
What value of \( x \) makes \( x - 1 = 3 \), and how can you use that to find \( f(3) \)?
06:47:10
Öğrenci
My answer is: 14
06:47:11
💭 AI Öğretmen
Let me review that answer
06:47:14
AI Öğretmen
Your answer was not correct, let me explain why.
06:47:16
AI Öğretmen
The function is given as \( f(x - 1) = 4x + 2 \), and we want to find \( f(3) \). Notice that the function’s input is \( x - 1 \), so to find \( f(3) \), we need to set \( x - 1 = 3 \).
06:47:20
AI Öğretmen
Solving \( x - 1 = 3 \) gives \( x = 4 \). Now, we substitute \( x = 4 \) into the right side of the equation: \( 4x + 2 = 4(4) + 2 = 16 + 2 = 18 \).
06:47:22
AI Öğretmen
A common mistake is to directly substitute 3 into the formula \( 4x + 2 \) without adjusting for the \( x - 1 \) inside the function. Remember, the function’s input is shifted by 1, so you must solve for \( x \) first.
06:47:25
AI Öğretmen
For example, if \( f(x - 1) = 4x + 2 \), then \( f(0) \) would require \( x - 1 = 0 \) so \( x = 1 \), and then \( f(0) = 4(1) + 2 = 6 \). This shows how the input shifts the value of \( x \).
06:47:26
AI Öğretmen
Therefore, the correct answer should be \( f(3) = 18 \).
06:47:26
AI Öğretmen
Should we continue with the lecture?
06:48:22
Öğrenci
Alright, let's continue
06:48:23
💭 AI Öğretmen
Moving on now
06:48:34
AI Öğretmen
In this lesson, we covered the definition of a function as a relation where every input in the domain maps to exactly one output in the codomain. We also discussed the roles of domain, codomain, and range, and how to determine if a relation is a function by checking that each input has one unique output. Additionally, we looked at examples illustrating these concepts. Do you have any questions about these topics? If not, I’ll end the lesson.
06:49:53
Öğrenci
can you give me another question
06:50:05
AI Öğretmen
Sure! Here’s a question for you: Consider the relation \( f: \{a, b, c\} \to \{1, 2, 3, 4\} \) defined by the mappings: - \( a \to 2 \) - \( b \to 3 \) - \( c \to 3 \) Is this relation a function? Explain why or why not. Did you understand the question? Would you like a hint before answering?
06:50:34
Öğrenci
this is a function.
06:50:41
AI Öğretmen
See you in the next lesson!

Voltran Okul Analiz Sistemi