← Ana Rapor / Ömer Betil EROL / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:51
Bitiş
Devam ediyor
Süre
8 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Kazanımlar:
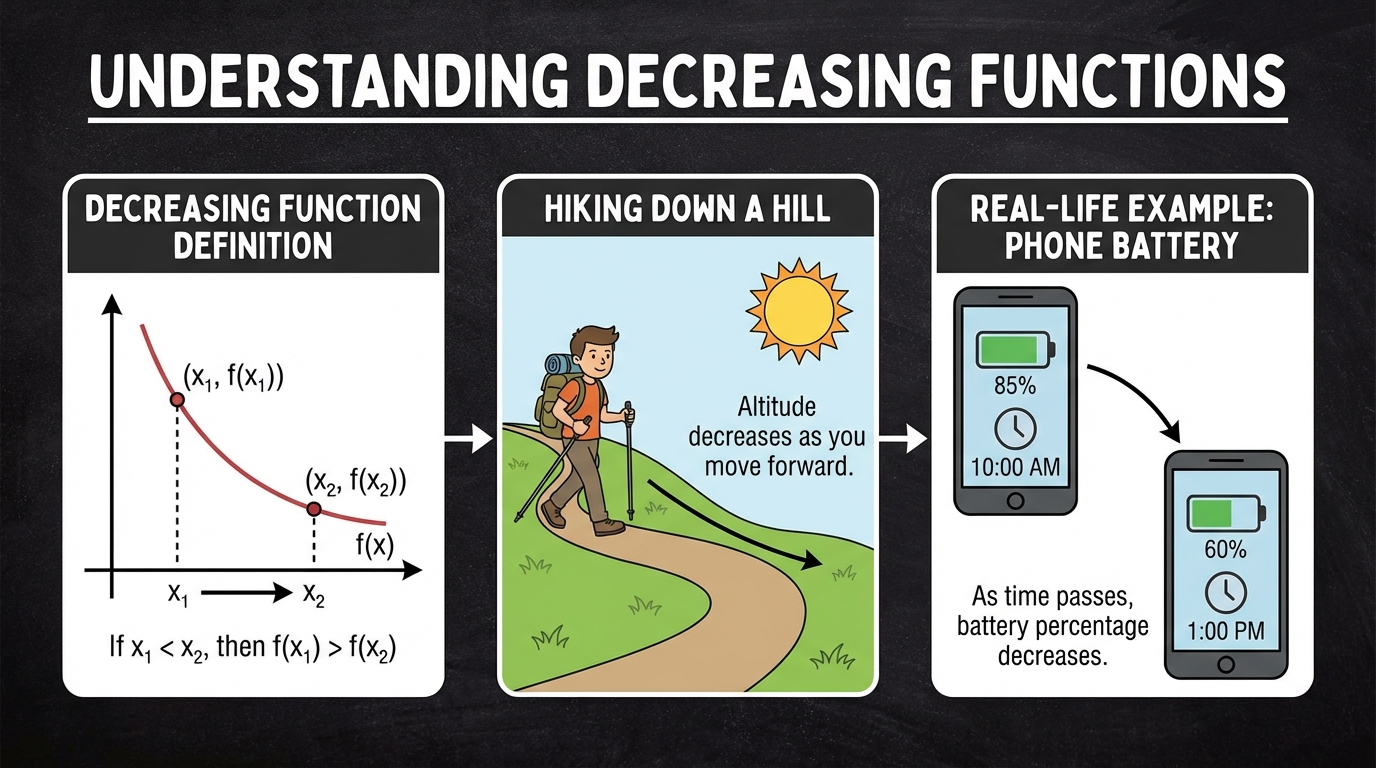
  • 2.1.c. Increasing and Decreasing Intervals of a Function

Detaylı Değerlendirme

Öğrenci Performans Analizi

Öğrenci, dersin başında konunun detaylı anlatılmasını isteyerek derse ilgili bir başlangıç yapmıştır. Ancak, ders boyunca teorik açıklamaları anladığını belirtmesine ("I got it") rağmen, bu anlama seviyesini pratik uygulamaya dökememiştir.

Öğrencinin temel zorluğu, bir fonksiyonun grafiğini analiz ederek artan ve azalan aralıkları doğru bir şekilde tespit etmekte yatmaktadır.

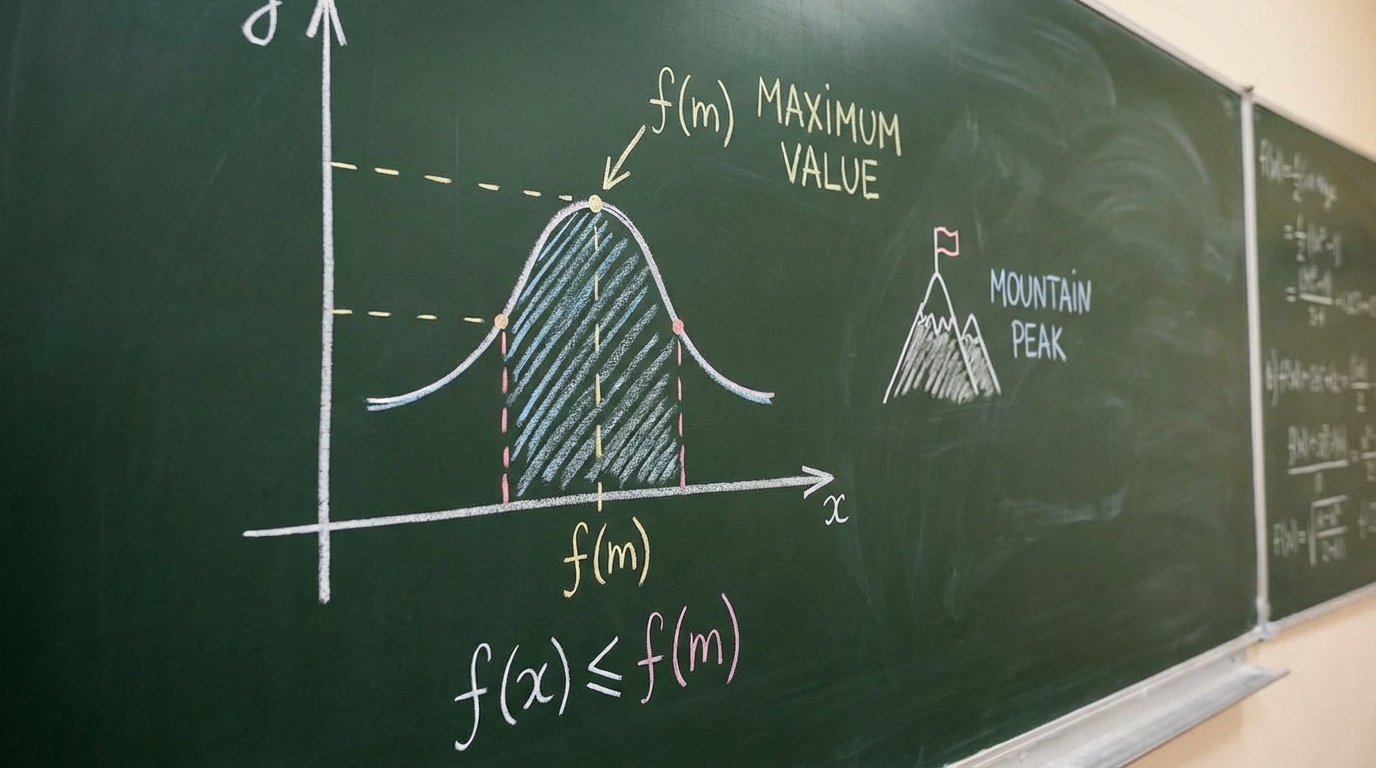
- Artan Aralık Sorusu: Öğrenciden grafiğin arttığı aralıkları bulması istendiğinde, hem artan hem de azalan kısımları içeren tek bir birleşik aralık (`(-5, 2)`) cevabını vermiştir. Bu, fonksiyonun davranışının değiştiği kritik noktaları (örneğin, yerel maksimum ve minimum) gözden kaçırdığını ve birden fazla artan aralık olabileceği konseptini anlamadığını göstermektedir.
- Azalan Aralık Sorusu: Benzer şekilde, fonksiyonun azalan olduğu aralığı bulması istendiğinde, yine hem azalan hem de artan bir bölümü içeren yanlış bir aralık (`[-2, 2]`) belirtmiştir. Bu durum, artan ve azalan fonksiyon davranışını grafikte ayırt etme konusunda tutarlı bir sorun yaşadığını teyit etmektedir.

Sonuç olarak, öğrenci fonksiyonun grafiğini soldan sağa okuma ve y-değerlerindeki değişime göre fonksiyonun davranışını (artıyor mu, azalıyor mu) yorumlama konusunda temel eksikliklere sahiptir. Açıklamaları anladığını düşünse de, bu bilgiyi problem çözümünde kullanamamaktadır.

📜 Oturum Detayları

06:51:22
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:51:22
💭 AI Öğretmen
Let us begin shortly
06:51:22
Görsel
Görsel
06:51:25
AI Öğretmen
Graphs in mathematics are read from the left side to the right side, much like how you read words in an English sentence.
06:51:26
AI Öğretmen
This left-to-right way of looking at graphs helps us understand what is happening with a function as we move along the x-axis.
06:51:27
AI Öğretmen
If we want to compare two different x-values on a graph, we always move from the left one to the right one.
06:51:28
AI Öğretmen
By doing this, we can see if the values of the function are going up or down as we move from one x-value to another.
06:51:29
AI Öğretmen
Knowing this direction makes it easier to talk about where the function is increasing or decreasing.
06:51:32
AI Öğretmen
We use this left-to-right view to describe when a graph goes up (increasing) or down (decreasing) between two x-values.
06:51:34
AI Öğretmen
Keeping this in mind helps us better find and talk about the parts of the graph where the function is increasing or decreasing.
06:51:35
AI Öğretmen
Did you understand how reading the graph from left to right helps us find increasing and decreasing intervals?
06:52:14
Öğrenci
I got it
06:52:15
💭 AI Öğretmen
Great, moving forward now
06:52:16
🎥 Video
06:52:17
AI Öğretmen
Did you understand how an increasing interval works in a function?
06:52:56
Öğrenci
I got it
06:53:01
💭 AI Öğretmen
Let us proceed carefully
06:53:02
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_33e16c0c-dc3a-47bd-91c9-e1d47eecd95c.png) Example: The graph of f is shown on the below. Find the intervals of x for which f(x) is **increasing**.
06:54:24
Öğrenci
My answer is: (-5,2)
06:54:25
💭 AI Öğretmen
Noted your answer
06:54:29
AI Öğretmen
Your answer was not correct, let me explain why the intervals where the function is increasing are different.
06:54:31
AI Öğretmen
To find where a function is increasing, we look at the parts of the graph where the curve goes up as we move from left to right. This means the y-values get bigger when x increases.
06:54:34
AI Öğretmen
In the graph, from x = -5 to x = -2, the function goes up, so it is increasing there. Then, from x = -2 to x = 0, the function goes down, so it is not increasing. After that, from x = 0 to x = 3, the function goes up again, so it is increasing there too.
06:54:36
AI Öğretmen
Your answer (-5, 2) is incorrect because it combines parts where the function actually decreases (between -2 and 0) and misses the second increasing interval from 0 to 3. Also, the correct intervals include the endpoints, so they are written with square brackets.
06:54:38
AI Öğretmen
For example, if a function goes up from 1 to 4, then down from 4 to 6, and up again from 6 to 8, the increasing intervals are [1, 4] and [6, 8], not one continuous interval.
06:54:40
AI Öğretmen
Therefore, the correct answer should be the union of two intervals: [-5, -2] and [0, 3].
06:54:40
AI Öğretmen
Should we continue with the lecture?
06:55:46
Öğrenci
Alright, let's continue
06:55:47
💭 AI Öğretmen
Let us proceed then
06:55:52
Görsel
Görsel
06:55:57
AI Öğretmen
A function is called decreasing on an interval when, if you pick any two numbers where $x_1$ is less than $x_2$, the value of the function at $x_1$ is greater than its value at $x_2$.
06:55:58
AI Öğretmen
Think of it like walking down a hill: as you move forward, your height gets lower.
06:55:59
AI Öğretmen
Another example is your phone's battery during the day, which usually drops as time goes on—this is just like a decreasing function.
06:55:59
AI Öğretmen
Did that explanation about decreasing functions make sense to you?
06:56:26
Öğrenci
I got it
06:56:29
💭 AI Öğretmen
Let us review this concept
06:56:30
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_fb69fa74-e294-4d91-a021-e549025bd3c4.png) Example: The graph of $f$ is shown on the above. Find the intervals of $x$ for which $f(x)$ is **decreasing**.
06:57:32
Öğrenci
My answer is: [-2,2]
06:57:33
💭 AI Öğretmen
Let me review that answer
06:57:37
AI Öğretmen
Your answer was not correct, let me explain why the interval [-2, 2] is not the right one for the decreasing part of the function.
06:57:39
AI Öğretmen
A function is decreasing where its graph goes down as you move from left to right, meaning the y-values get smaller. Looking at the graph, from -2 to 0 the graph goes down, but from 0 to 2 it actually goes up again.
06:57:42
AI Öğretmen
So, the function decreases only on the interval [-2, 0], not beyond 0 because after that the function is increasing. The mistake might be thinking the function keeps going down past 0, but it actually rises.
06:57:45
AI Öğretmen
For example, at x = -1, the y-value is less than at x = -2 (decreasing), but at x = 1, the y-value is greater than at x = 0 (increasing). Therefore, the correct answer should be [-2, 0].
06:57:45
AI Öğretmen
Should we continue with the lecture?
06:58:30
Öğrenci
Alright, let's continue
06:58:31
💭 AI Öğretmen
Moving to next step
06:58:34
Görsel
Görsel
06:58:39
AI Öğretmen
The maximum value of a function means the largest number you can get as an answer when you put values into the function, but only considering a certain interval or part of the function.
06:58:40
AI Öğretmen
Mathematically, $f(m)$ is called a maximum if, for every $x$ value in our interval, $f(x)$ is always less than or equal to $f(m)$.
06:58:43
AI Öğretmen
This means $f(m)$ is the biggest output you will get on that specific interval, and it is sometimes called the absolute maximum on the interval.
06:58:44
AI Öğretmen
If you draw the graph of a function, the maximum looks like the very top point or the "peak", similar to the highest part of a mountain.
06:58:46
AI Öğretmen
At the maximum point, the function stops getting higher and starts to go down.
06:58:48
AI Öğretmen
Not every function will have a maximum in each interval, but if it does, you can spot it because it is the highest point, just like standing at the top of a hill or mountain and seeing that you cannot go any higher.
06:58:48
AI Öğretmen
Do you feel clear about how to identify the maximum value of a function on an interval?
06:59:40
Öğrenci
I got it
06:59:43
💭 AI Öğretmen
Let's review this concept
06:59:43
❓ Soru basic
**Example:** The graph of $g$ is shown below. Find the intervals of $x$ for which $g(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?** ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_11a805a3-b66d-431d-99b4-450c738ea61d.png)

Voltran Okul Analiz Sistemi