← Ana Rapor / Alara Hira AKYAZICI / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:27
Bitiş
02 December 2025, 06:43
Süre
15 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Detaylı Değerlendirme

Genel Değerlendirme
Öğrenci, "Fonksiyonların Tanımı" konusunda mükemmel bir performans sergilemiştir. Dersin başında konuyu detaylı bir şekilde açıklanmasını istemesine rağmen, sonraki tüm açıklamalara "Anladım" şeklinde olumlu yanıt vermiş ve sorulan tüm soruları doğru ve eksiksiz bir şekilde çözmüştür.

Detaylı Analiz
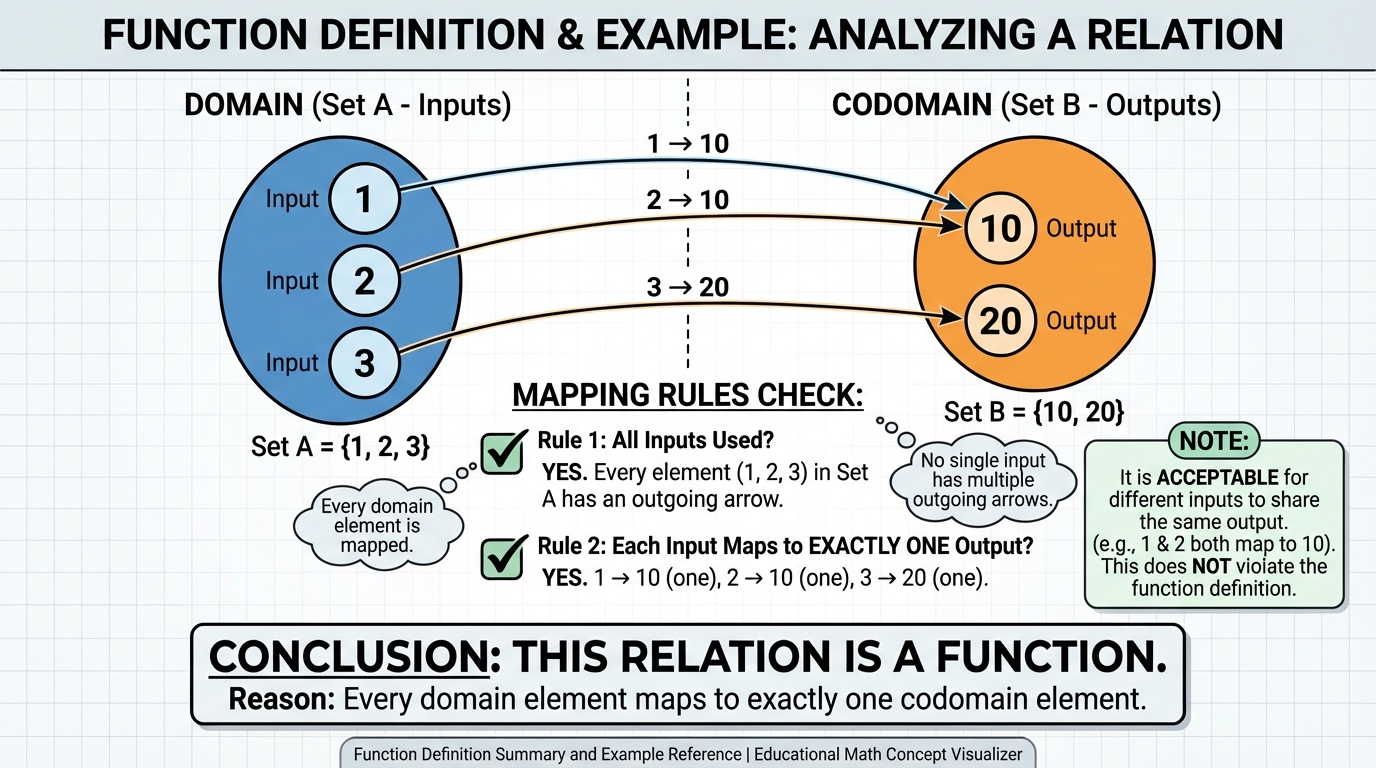
- Kavramsal Anlama: Öğrenci; tanım kümesi, değer kümesi ve görüntü kümesi gibi temel kavramları doğru bir şekilde tanımlayabilmektedir. Şema ile verilen bir fonksiyonda bu kümeleri hatasız bir şekilde tespit etmiştir.
- Uygulama Becerisi: Öğrenci, bir bağıntının fonksiyon olup olmadığını belirleme konusunda yetkindir. Özellikle tanım ve değer kümelerinin (Doğal sayılardan doğal sayılara) fonksiyon olma şartını nasıl etkilediğini kendi verdiği doğru bir örnekle açıklamıştır. Rasyonel bir ifadenin en geniş tanım kümesini ve bir fonksiyonun belirli bir değer için görüntüsünü bulma gibi farklı soru tiplerini de başarıyla çözmüştür.
- Öğrenme Davranışı: Öğrenci, ders boyunca konuya odaklanmış ve olumlu bir tutum sergilemiştir. Anlamadığı bir nokta olmamış, ek bir açıklamaya veya ipucuna ihtiyaç duymamıştır.

Sonuç
Öğrencinin bu derste işlenen "Fonksiyonların Tanımı" alt konusuyla ilgili herhangi bir eksiği bulunmamaktadır. Konuyu tam olarak anladığı ve farklı problem türlerine uygulayabildiği görülmektedir.

📜 Oturum Detayları

06:27:57
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:27:58
💭 AI Öğretmen
Great, preparing explanation now
06:27:58
🎥 Video
06:27:59
AI Öğretmen
Did you understand how a function relates elements from Set A to Set B?
06:28:49
Öğrenci
I got it
06:28:51
💭 AI Öğretmen
Let's continue then
06:28:52
🎥 Video
06:28:52
AI Öğretmen
Do you feel clear about the differences between domain, codomain, and range?
06:29:29
Öğrenci
I got it
06:29:33
💭 AI Öğretmen
Let us continue shortly
06:29:33
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:30:31
Öğrenci
My answer is: Domain:-1,0,1,2 Codomain:0,1,2,3,4,5 Range:0,1,4
06:30:31
💭 AI Öğretmen
Good, checking now
06:30:37
AI Öğretmen
That's absolutely fantastic! You've correctly identified all three parts of the function.
06:30:39
AI Öğretmen
You nailed it by recognizing that the **domain** is all the input values in set A, the **codomain** is the entire target set B, and the **range** is just the specific values in B that actually get mapped to by the function.
06:30:40
AI Öğretmen
This shows you have a great understanding of how to interpret function diagrams!
06:30:41
AI Öğretmen
Should we continue with the lecture?
06:31:02
Öğrenci
Alright, let's continue
06:31:03
💭 AI Öğretmen
Let's proceed shortly
06:31:12
Görsel
Görsel
06:31:15
AI Öğretmen
A relation is considered a function if it follows a specific rule.
06:31:17
AI Öğretmen
Every input, which means each element in the Domain or Set A, must be paired with one output in the Codomain, also known as Set B.
06:31:20
AI Öğretmen
It's important to remember that not every element in the Codomain needs to have a match; there can be outputs that are not connected to any input.
06:31:22
AI Öğretmen
More than one input can share the same output, which is called a many-to-one mapping.
06:31:25
AI Öğretmen
However, one-to-many mapping is not allowed, so a single input can't be matched with multiple outputs.
06:31:28
AI Öğretmen
This means that a function will always assign exactly one output from the codomain to each input in the domain.
06:31:28
AI Öğretmen
Did this explanation make the concept of a function clear to you?
06:31:58
Öğrenci
I got it
06:32:00
💭 AI Öğretmen
Let us review this carefully
06:32:00
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:33:40
Öğrenci
My answer is: This is not a function if we give 2 to x 2=x Then it would be: 2-3=-1 -1 is not element of natural numbers
06:33:41
💭 AI Öğretmen
Let me review that closely
06:33:47
AI Öğretmen
Fantastic job! You've hit the nail on the head!
06:33:48
AI Öğretmen
You're absolutely right that for a relation to be a function from natural numbers to natural numbers, every input from the natural numbers must result in an output that is also a natural number.
06:33:49
AI Öğretmen
Your example with $x=2$ perfectly illustrates how $f(x) = x-3$ produces $-1$, which isn't in the set of natural numbers (the codomain).
06:33:50
AI Öğretmen
This shows a great understanding of how the domain and codomain define whether a relation is a true function!
06:33:52
AI Öğretmen
Therefore, the correct answer is No, it is not a function.
06:33:52
AI Öğretmen
Should we continue with the lecture?
06:34:24
Öğrenci
Alright, let's continue
06:34:25
💭 AI Öğretmen
Moving forward now
06:34:33
Görsel
Görsel
06:34:35
AI Öğretmen
A relation between two sets can be analyzed to see if it is a function by following certain rules.
06:34:37
AI Öğretmen
Suppose we have two sets, Set A (Inputs), which has the numbers 1, 2, and 3, and Set B (Outputs), which has the numbers 10 and 20.
06:34:38
AI Öğretmen
The relationships or mappings are: 1 maps to 10, 2 maps to 10, and 3 maps to 20.
06:34:39
AI Öğretmen
Notice that each input from Set A, which are 1, 2, and 3, is matched with some output in Set B.
06:34:40
AI Öğretmen
In these mappings, it is fine to have different inputs, like 1 and 2, both connect to the same output, which is 10.
06:34:41
AI Öğretmen
The important thing is that each input is matched with only one output.
06:34:42
AI Öğretmen
So, the conclusion is that this relation is a function because every domain element, or input, connects to exactly one codomain element, or output.
06:34:44
AI Öğretmen
Did you understand why this relation qualifies as a function?
06:36:03
Öğrenci
I got it
06:36:06
💭 AI Öğretmen
Let us review this carefully
06:36:07
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:37:29
Öğrenci
My answer is: x+2=0 x=-2 All the real numbers except -2
06:37:30
💭 AI Öğretmen
Let me review that answer
06:37:34
AI Öğretmen
That's absolutely spot on! You did a fantastic job of identifying the critical point for this function.
06:37:35
AI Öğretmen
You correctly understood that the denominator of a fraction can never be zero, as that would make the function undefined.
06:37:36
AI Öğretmen
This shows you really grasp how to find the domain of rational functions by looking for these important restrictions!
06:37:37
AI Öğretmen
Keep up the amazing work!
06:37:38
AI Öğretmen
Therefore, the correct answer is $\{x \in \mathbb{R} \mid x \neq -2\}$.
06:37:38
AI Öğretmen
Should we continue with the lecture?
06:38:11
Öğrenci
Alright, let's continue
06:38:12
💭 AI Öğretmen
Continuing with the lesson now
06:38:20
AI Öğretmen
A relation is a function only when each input from the domain is linked to one and only one output in the codomain.
06:38:21
AI Öğretmen
This means for every value you use as an input, you can't have two different outputs connected to it.
06:38:22
AI Öğretmen
However, it's okay if different inputs have the same output; outputs can be shared among multiple inputs in a function.
06:38:23
AI Öğretmen
So, the main requirement for a function is the uniqueness of the output for each input in the domain.
06:38:24
AI Öğretmen
Did you understand how to tell if a relation is a function?
06:39:14
Öğrenci
I got it
06:39:16
💭 AI Öğretmen
Let us review this briefly
06:39:16
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:41:21
Öğrenci
My answer is: x-1=3 x=4 =4x4+2 =16+2 =18
06:41:21
💭 AI Öğretmen
Let me review your steps
06:41:26
AI Öğretmen
Fantastic job! You absolutely nailed it!
06:41:28
AI Öğretmen
You correctly understood that to find $f(3)$, you need to set the expression inside the parentheses, $x-1$, equal to 3.
06:41:30
AI Öğretmen
This allowed you to find the correct value for $x$ and then substitute it back into the function's rule to get the right answer. Great work with function evaluation!
06:41:31
AI Öğretmen
Therefore the correct answer is 18.
06:41:31
AI Öğretmen
Should we continue with the lecture?
06:41:49
Öğrenci
Alright, let's continue
06:41:50
💭 AI Öğretmen
Moving ahead now
06:41:59
AI Öğretmen
In this lesson, we covered the definition of a function as a relation where each input from the domain has exactly one output in the codomain. We also discussed the roles of domain, codomain, and range, and how to determine if a relation is a function by checking if every input maps to one output. Additionally, we looked at examples showing that multiple inputs can share the same output, but one input cannot have multiple outputs. Do you have any questions about these concepts? If not, I’ll end the lesson here.
06:43:10
Öğrenci
Hocam.
06:43:16
AI Öğretmen
See you in the next lesson!

Voltran Okul Analiz Sistemi