AI Etüt Oturumu
Oturum Bilgileri
AI Öğretmen Değerlendirmesi
Detaylı Değerlendirme
Genel Değerlendirme
Öğrenci derse ilgili ve öğrenmeye istekli bir başlangıç yaptı. Konunun temel tanımını dinledikten sonra, bir fonksiyonun bire bir olup olmadığını nasıl test edeceğine dair proaktif ve yerinde bir soru sordu. Bu, öğrencinin konuyu sadece dinlemekle kalmayıp, aynı zamanda pratik uygulamasını da anlamaya çalıştığını göstermektedir.
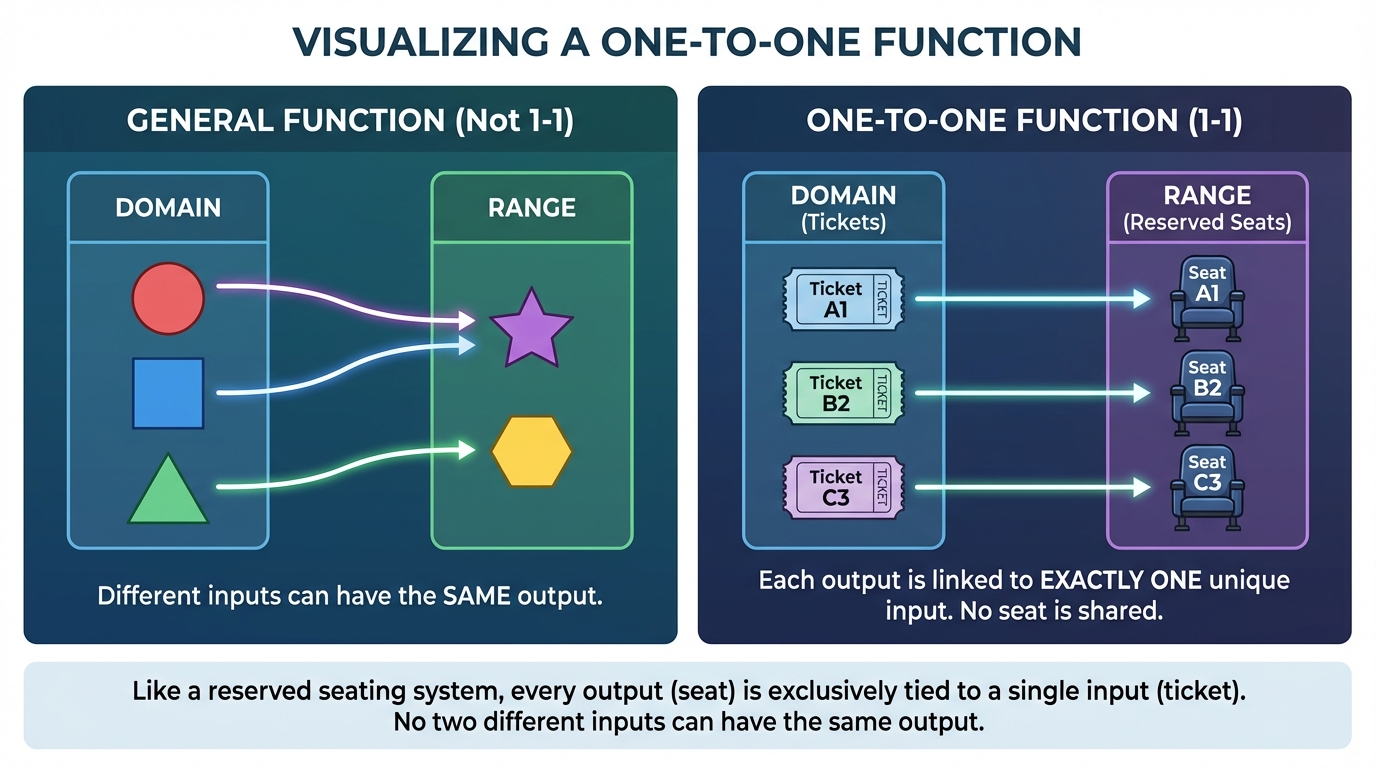
AI öğretmenin "yatay doğru testi" gibi yöntemleri açıklamasının ardından, öğrenciye sunulan örnek soruyu (girdiler ve çıktıları verilen bir fonksiyonun bire bir olup olmadığını belirleme) doğru bir şekilde cevapladı. Bu, öğrencinin bir fonksiyonun bire bir olması için "her farklı girdinin farklı bir çıktıya sahip olması gerektiği" temel kuralını anladığını ve uygulayabildiğini kanıtlamaktadır.
Öğrencinin İyi Olduğu Konular
Öğrenci, bire bir fonksiyonun tanımını anlama ve bu tanımı verilen bir örnek üzerinde uygulama konusunda başarılı bir performans sergiledi.
* İyi Olduğu Konular:
* Introduction to Functions and Linear Functions
* İyi Olduğu Alt Konular:
* 2.1.d. One to One Function
Öğrencinin Zorlandığı Konular
Bu derste öğrencinin herhangi bir konuda belirgin bir eksikliği veya zorluk yaşadığı gözlemlenmemiştir. Sorduğu soru, konuyu daha derinlemesine anlama çabasının bir parçası olarak değerlendirilmiştir.
* Eksiklik Saptanan Konular:
* *Bu derste öğrencinin eksikliği olan bir konu saptanmadı.*
* Eksiklik Saptanan Alt Konular:
* *Bu derste öğrencinin eksikliği olan bir alt konu saptanmadı.*
* Eksiklik Saptanan Kazanımlar:
* *Bu derste öğrencinin eksikliği olan bir kazanım saptanmadı.*
Ders Dışı Yorumlar
Öğrencinin ders dışı herhangi bir sorusu veya yorumu olmamıştır.