← Ana Rapor / Mert KILIÇ / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:35
Bitiş
Devam ediyor
Süre
13 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Detaylı Değerlendirme

Genel Değerlendirme
Öğrenci derse konunun detaylı bir şekilde anlatılmasını isteyerek başladı. Bu, öğrenme konusunda istekli olduğunu gösteriyor. Ders boyunca, öğrenci öğretmenin açıklamalarından sonra sorulan tüm soruları doğru ve kendinden emin bir şekilde yanıtladı. Performansı oldukça başarılıydı.

Öğrencinin İyi Olduğu Konular
Öğrenci, fonksiyonların temel tanımları konusunda sağlam bir anlayış sergiledi.
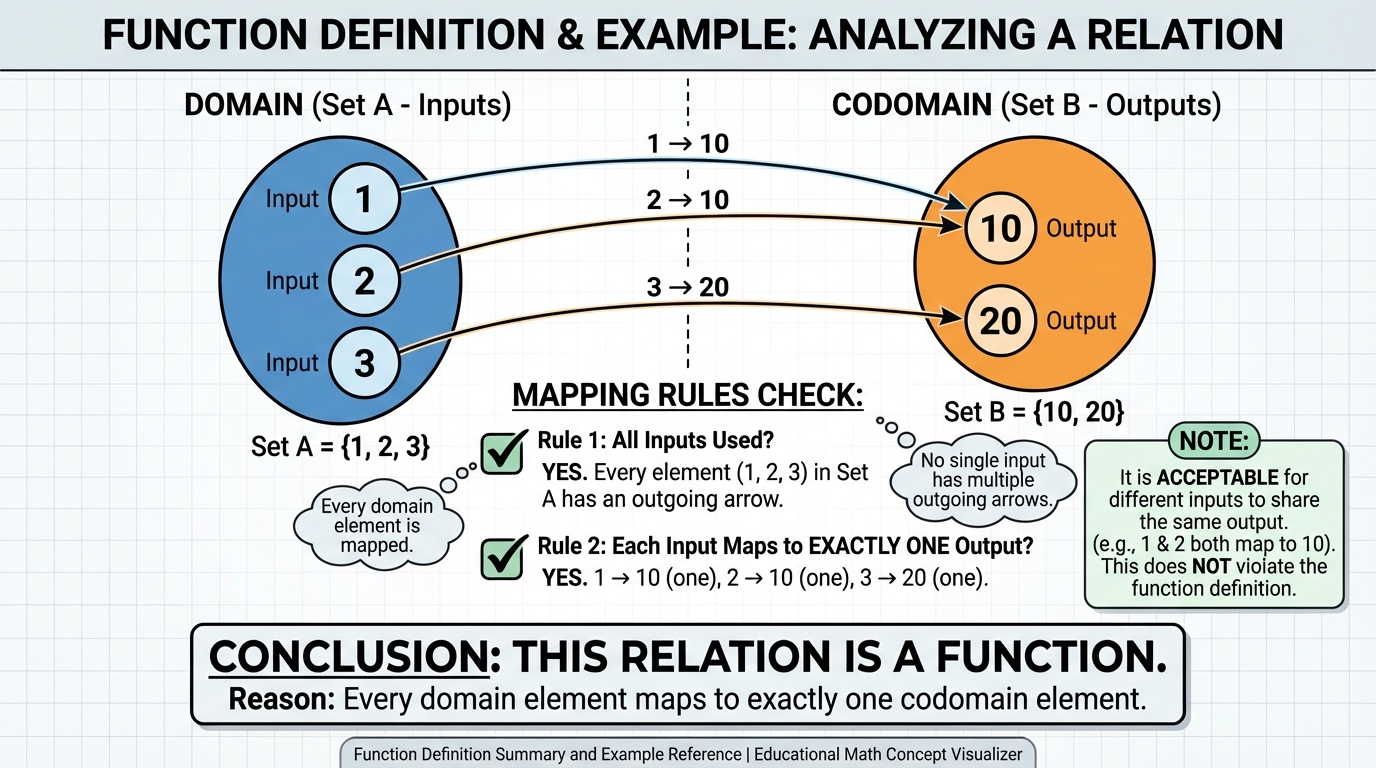
* Domain, Codomain ve Range: Verilen bir fonksiyon için tanım kümesi (domain), değer kümesi (codomain) ve görüntü kümesini (range) doğru bir şekilde tespit etti.
* Fonksiyon Olma Şartları: Bir bağıntının fonksiyon olup olmadığını belirlemede başarılıydı. Özellikle, bir bağıntının çıktısının belirtilen değer kümesi (codomain) içinde olması gerektiği kuralını doğru bir şekilde uyguladı.
* Tanım Kümesi Bulma: Rasyonel bir ifadede paydayı sıfır yapan değeri bularak fonksiyonun en geniş tanım kümesini doğru bir şekilde belirledi.

Öğrencinin Zorlandığı Konular
Bu ders seansında öğrencinin herhangi bir konuda zorlandığı veya eksiklik gösterdiği gözlemlenmemiştir. Sorulan tüm sorulara doğru ve açıklayıcı yanıtlar vermiştir.

Ders Dışı Konuşmalar
Ders sırasında konu dışı herhangi bir yorum veya soru kaydedilmemiştir.

📜 Oturum Detayları

06:35:11
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:35:12
💭 AI Öğretmen
Great, preparing details now
06:35:12
🎥 Video
06:35:14
AI Öğretmen
Did you understand how a function assigns each element in Set A to exactly one element in Set B?
06:35:52
Öğrenci
I got it
06:35:53
💭 AI Öğretmen
Very well noted
06:35:54
🎥 Video
06:35:55
AI Öğretmen
Did the explanation about domain, codomain, and range make sense to you?
06:36:36
Öğrenci
I got it
06:36:38
💭 AI Öğretmen
Let us proceed soon
06:36:38
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:38:37
Öğrenci
My answer is: Domain: {-1, 0, 1, 2} Codomain: {0, 1, 2, 3, 4, 5} Range: {0, 1, 4}
06:38:38
💭 AI Öğretmen
Reviewing your response
06:38:43
AI Öğretmen
Fantastic job! You've perfectly identified the domain, codomain, and range of the function!
06:38:44
AI Öğretmen
You correctly understood that the domain is all the input values in set A, the codomain is all the possible output values in set B, and the range is the specific output values that are actually mapped to.
06:38:45
AI Öğretmen
It's great that you can distinguish between all possible outputs (codomain) and the actual outputs (range)! Keep up the excellent work!
06:38:46
AI Öğretmen
Therefore, the correct answer is Domain: $\\{-1, 0, 1, 2\\}$, Codomain: $\\{0, 1, 2, 3, 4, 5\\}$, Range: $\\{0, 1, 4\\}$.
06:38:46
AI Öğretmen
Should we continue with the lecture?
06:39:19
Öğrenci
Alright, let's continue
06:39:20
💭 AI Öğretmen
Preparing next segment
06:39:26
Görsel
Görsel
06:39:28
AI Öğretmen
A relation is considered a function if it follows a certain rule.
06:39:31
AI Öğretmen
This rule states that every input, which is an element from the Domain or Set A, must be matched to some output in the Codomain, known as Set B.
06:39:33
AI Öğretmen
It's important to know that not every element in the Codomain needs to have an input matched to it, so it's okay if there are elements in Set B that aren't paired with anything from Set A.
06:39:35
AI Öğretmen
Multiple different inputs from the domain can be assigned to the same output in the codomain, which means many-to-one mappings are allowed for functions.
06:39:37
AI Öğretmen
However, a single input cannot be assigned to more than one output; one-to-many mappings are not allowed.
06:39:39
AI Öğretmen
This means a function gives exactly one value in the codomain for each element in the domain.
06:39:40
AI Öğretmen
Does this definition of a function make sense to you so far?
06:40:16
Öğrenci
I got it
06:40:18
💭 AI Öğretmen
Good, let's proceed.
06:40:19
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:43:25
Öğrenci
My answer is: No, because if we let the domain be 1, then the codomain would be -2, which is not a Natural number that makes it not a function.
06:43:26
💭 AI Öğretmen
Let me review that answer
06:43:31
AI Öğretmen
That's absolutely right!
06:43:32
AI Öğretmen
You've hit the nail on the head by pointing out that for $x=1$, the output $f(1) = -2$ is not a natural number.
06:43:33
AI Öğretmen
For a relation to be a function, every element in the domain must map to an element *within* the specified codomain. Great job understanding this key concept!
06:43:34
AI Öğretmen
Therefore, the correct answer is No.
06:43:34
AI Öğretmen
Should we continue with the lecture?
06:44:07
Öğrenci
Alright, let's continue
06:44:08
💭 AI Öğretmen
Continuing now
06:44:14
Görsel
Görsel
06:44:17
AI Öğretmen
A relation between two sets can be analyzed to determine if it is a function by checking specific rules.
06:44:19
AI Öğretmen
Consider two sets: Set A, which we will use as Inputs, is $\{1, 2, 3\}$, and Set B, which we will use as Outputs, is $\{10, 20\}$.
06:44:21
AI Öğretmen
The mappings between these sets are as follows: $1$ maps to $10$, $2$ maps to $10$, and $3$ maps to $20$.
06:44:23
AI Öğretmen
We see that each element in Set A, which are $1$, $2$, and $3$, is used in the mapping, so no input is left out.
06:44:24
AI Öğretmen
Each input is matched to only one output, meaning no input goes to two different outputs.
06:44:26
AI Öğretmen
It is acceptable for different inputs to share the same output; in this example, both $1$ and $2$ are mapped to $10$.
06:44:27
AI Öğretmen
In conclusion, this relation is a function because every element in the domain (Set A) is paired with exactly one element in the codomain (Set B).
06:44:28
AI Öğretmen
Did you understand why this relation qualifies as a function?
06:46:02
Öğrenci
I got it
06:46:05
💭 AI Öğretmen
Let us proceed carefully
06:46:05
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:47:33
Öğrenci
My answer is: Domain: R / {-2}
06:47:34
💭 AI Öğretmen
Noted your answer
06:47:38
AI Öğretmen
That's absolutely spot on! Fantastic job!
06:47:39
AI Öğretmen
You correctly identified that the denominator of a fraction cannot be zero, which is the key restriction for rational functions like this one.
06:47:40
AI Öğretmen
Understanding how to find these restrictions is crucial for determining the domain of a function, showing you really grasp this concept!
06:47:42
AI Öğretmen
Therefore, the correct answer is R / {-2}.
06:47:42
AI Öğretmen
Should we continue with the lecture?

Voltran Okul Analiz Sistemi