← Ana Rapor / Alya Deniz USTA / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:29
Bitiş
Devam ediyor
Süre
7 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
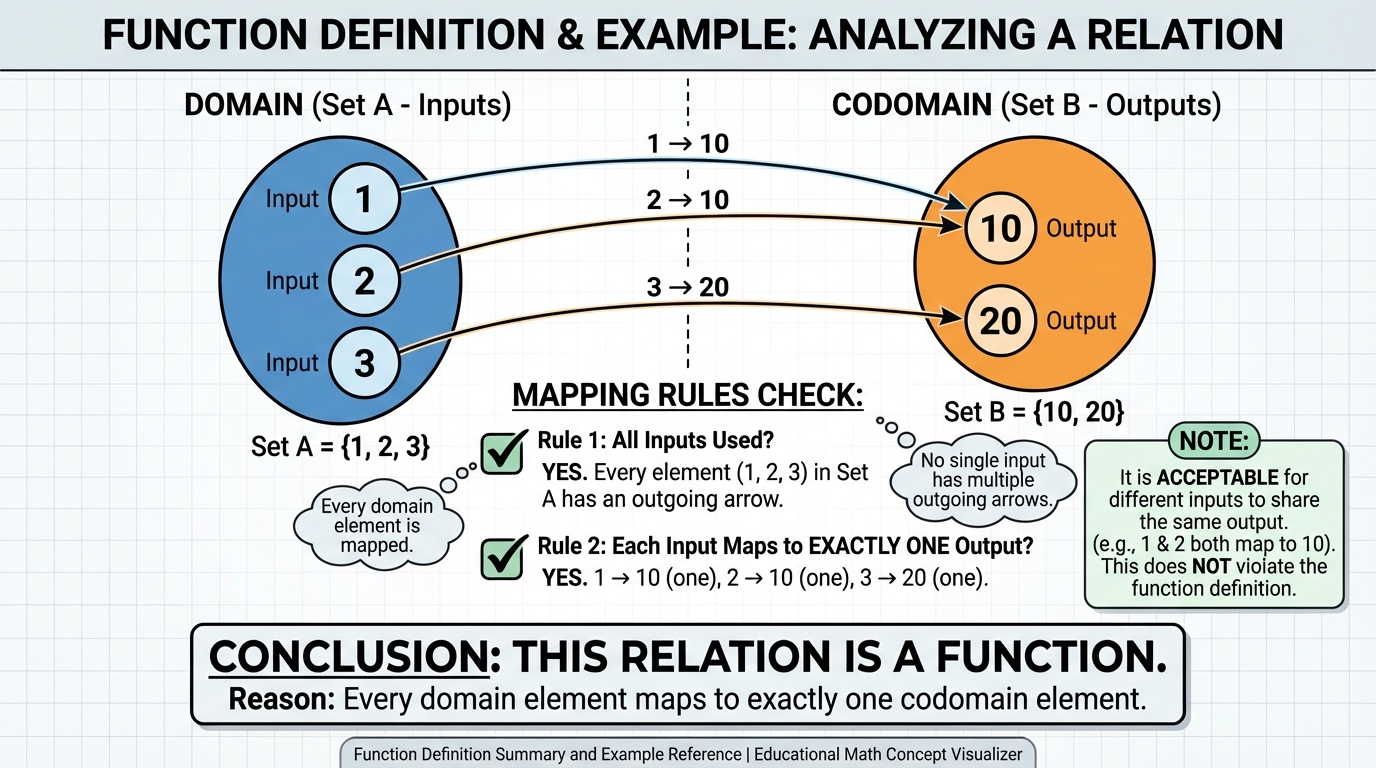
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci derse ilgili ve öğrenmeye istekli bir başlangıç yaptı. Dersin başında, bir fonksiyonun temel tanımına ilişkin ("Bir girdinin iki farklı çıktısı olursa ne olur?") kritik ve yerinde bir soru sordu. Bu durum, fonksiyon olmanın temel şartlarından biri olan "her girdinin yalnızca bir çıktısı olması" kuralını tam olarak anlamak için ek bir açıklamaya ihtiyaç duyduğunu göstermiştir.

Ancak, bu konsept kendisine açıklandıktan sonra öğrencinin performansı önemli ölçüde arttı.
- Tanım kümesi (domain), değer kümesi (codomain) ve görüntü kümesi (range) kavramlarını anladığını, sorulan soruda bu kümeleri hatasız bir şekilde bularak gösterdi.
- Verilen bir ifadenin, tanım ve değer kümeleri (doğal sayılardan doğal sayılara) göz önünde bulundurulduğunda neden bir fonksiyon olmadığını mantıklı bir gerekçe ile doğru bir şekilde açıkladı.

Sonuç olarak, öğrencinin fonksiyon tanımının temel mantığı konusunda başlangıçta küçük bir boşluğu olsa da, ders ilerledikçe konuyu anlama ve uygulama becerisi gösterdiği görülmektedir.

Hangi Konularda Eksiklikleri Var?

- topics_with_gaps:
- Introduction to Functions and Linear Functions
- subtopics_with_gaps:
- 2.1.a. Formal Definitions of Functions

Hangi Konularda İyi?

Öğrenci, tanım, değer ve görüntü kümesini belirleme gibi alt kazanımlarda başarılı olsa da, fonksiyonun temel tanımıyla ilgili başlangıçta yaşadığı kafa karışıklığı nedeniyle, konunun bütünü "eksiklikler" listesine eklenmiştir. Bu, konunun temelinde pekiştirme yapılması gerektiğini göstermektedir.

Tamamen Ders Dışı Sorular/Yorumlar

- Bu derste tamamen ders dışı bir soru veya yorum kaydedilmemiştir.

📜 Oturum Detayları

06:29:39
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:29:39
💭 AI Öğretmen
Great enthusiasm noted
06:29:39
🎥 Video
06:29:40
AI Öğretmen
Did you understand how a function maps each element of Set A to exactly one element of Set B?
06:31:21
Öğrenci
What happens if an element in Set A maps to two different elements in Set B?
06:31:23
💭 AI Öğretmen
Let me consider that carefully
06:31:27
AI Öğretmen
If an element in Set A maps to two different elements in Set B, then the relation is not a function. This is because a function requires each input to have exactly one output. So, having two outputs for one input breaks the rule of a function.
06:31:29
AI Öğretmen
This is why functions are special types of relations—they ensure a unique output for every input. Do you understand this concept?
06:31:40
Öğrenci
I got it
06:31:43
💭 AI Öğretmen
Let us continue then
06:31:43
🎥 Video
06:31:44
AI Öğretmen
Did you understand how the domain, codomain, and range relate to each other in a function?
06:32:15
Öğrenci
I got it
06:32:18
💭 AI Öğretmen
Let us proceed shortly
06:32:18
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:33:39
Öğrenci
My answer is: domain: -1,0,1,2 Codomain: 0,1,2,3,4,5 Range: 0,1,4
06:33:40
💭 AI Öğretmen
Noted your answer
06:33:43
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range of the function.
06:33:46
AI Öğretmen
You clearly understand that the domain is all possible inputs, the codomain is all possible outputs, and the range is the set of actual outputs that the function produces.
06:33:47
AI Öğretmen
It's great to see you distinguishing between the entire set B (codomain) and the specific values that are actually mapped to (range)! Keep up the excellent work!
06:33:48
AI Öğretmen
Therefore, the correct answer is Domain: $\{-1, 0, 1, 2\}$, Codomain: $\{0, 1, 2, 3, 4, 5\}$, Range: $\{0, 1, 4\}$.
06:33:48
AI Öğretmen
Should we continue with the lecture?
06:34:00
Öğrenci
Alright, let's continue
06:34:00
💭 AI Öğretmen
Proceeding with the lecture
06:34:13
Görsel
Görsel
06:34:15
AI Öğretmen
A relation is called a function if it follows an important rule.
06:34:17
AI Öğretmen
Every input, which means every element from the Domain or Set A, must be connected to some output in the Codomain, which is Set B.
06:34:19
AI Öğretmen
It is also important to know that not every element in Set B, the Codomain, needs to have an input mapped to it. This means it is okay to have some leftovers in the output.
06:34:21
AI Öğretmen
Multiple inputs, or elements from the Domain, can point to the same output in the Codomain. This is called many-to-one mapping, and it is allowed in functions.
06:34:23
AI Öğretmen
However, one-to-many mapping is not allowed. This means that an input from the Domain cannot be connected to more than one output in the Codomain.
06:34:24
AI Öğretmen
So, a function connects each input from the Domain to exactly one output in the Codomain, and not more than one.
06:34:25
AI Öğretmen
Did the explanation about what makes a relation a function make sense to you?
06:34:43
Öğrenci
I got it
06:34:45
💭 AI Öğretmen
Let us move forward
06:34:46
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:35:17
Öğrenci
My answer is: no,-3 is not on given domain of natural numbers
06:35:18
💭 AI Öğretmen
Let me review that answer
06:35:22
AI Öğretmen
That's absolutely right! Fantastic job!
06:35:25
AI Öğretmen
You correctly identified that for $f(x) = x - 3$ to be a function from natural numbers to natural numbers, every input $x$ from the domain ($\mathbb{N}$) must produce an output $f(x)$ that is also in the codomain ($\mathbb{N}$).
06:35:27
AI Öğretmen
Your point about -3 not being in the natural numbers is spot on, as inputs like 1 or 2 would result in negative numbers, which aren't natural numbers.
06:35:28
AI Öğretmen
This shows you really understand the importance of both the domain and codomain when defining a function! Keep up the great work!
06:35:29
AI Öğretmen
Therefore, the correct answer is No, it is not a function.
06:35:29
AI Öğretmen
Should we continue with the lecture?
06:35:43
Öğrenci
Alright, let's continue
06:35:44
💭 AI Öğretmen
Continuing with the lecture
06:35:49
Görsel
Görsel
06:35:51
AI Öğretmen
A relation between two sets can be checked to see if it is a function by using specific rules.
06:35:52
AI Öğretmen
Take Set A, which has the values 1, 2, and 3 as inputs, and Set B, which has 10 and 20 as possible outputs.
06:35:54
AI Öğretmen
The given mappings are 1 goes to 10, 2 goes to 10, and 3 goes to 20.
06:35:56
AI Öğretmen
Each input in Set A (which are 1, 2, and 3) is assigned to an output in Set B, so all inputs are used.
06:35:58
AI Öğretmen
Also, every input is connected to only one output, which means we do not have any input pointing to more than one output.
06:35:59
AI Öğretmen
It is fine for different inputs to have the same output, like 1 and 2 both going to 10.
06:36:01
AI Öğretmen
In conclusion, this relation is a function because each element from the input set is paired with exactly one output.
06:36:02
AI Öğretmen
Did you understand why this relation qualifies as a function?
06:36:47
Öğrenci
I got it
06:36:49
💭 AI Öğretmen
Let us review this carefully
06:36:49
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$

Voltran Okul Analiz Sistemi