← Ana Rapor / Yaman Arhan KOCA / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:48
Bitiş
Devam ediyor
Süre
17 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
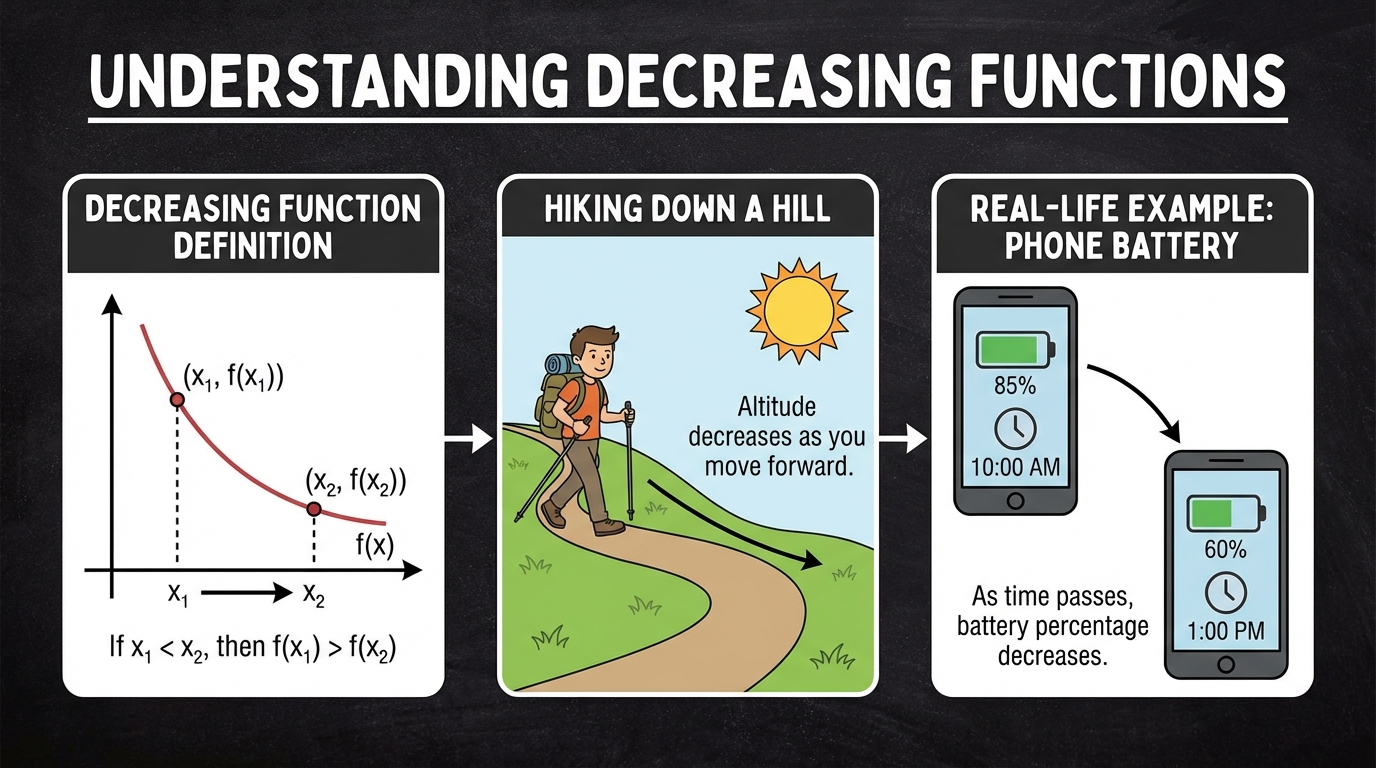
  • 2.1.c. Increasing and Decreasing Intervals of a Function

Detaylı Değerlendirme

Genel Değerlendirme
Öğrenci, "Bir Fonksiyonun Artan ve Azalan Aralıkları" konusuna genel olarak hakim ancak aralık gösterimi ve uç noktaların dahil edilmesi gibi temel bir noktada eksikliği bulunmaktadır. Dersin başında konunun detaylı anlatılmasını istemesi, öğrenme konusunda istekli olduğunu göstermektedir. İlk soruda yaptığı hatayı, öğretmenin açıklamasından sonraki sorularda tekrar etmemesi, konuyu anladığını ve geri bildirimlerden faydalandığını göstermektedir.

Güçlü Yönler
- Azalan Aralıkları Belirleme: Öğrenci, bir fonksiyonun grafiğine bakarak azalan olduğu aralığı doğru bir şekilde `[-2,0]` olarak tespit etmiştir. Bu, grafiği soldan sağa doğru okuyabildiğini ve fonksiyonun davranışını doğru yorumladığını gösterir.
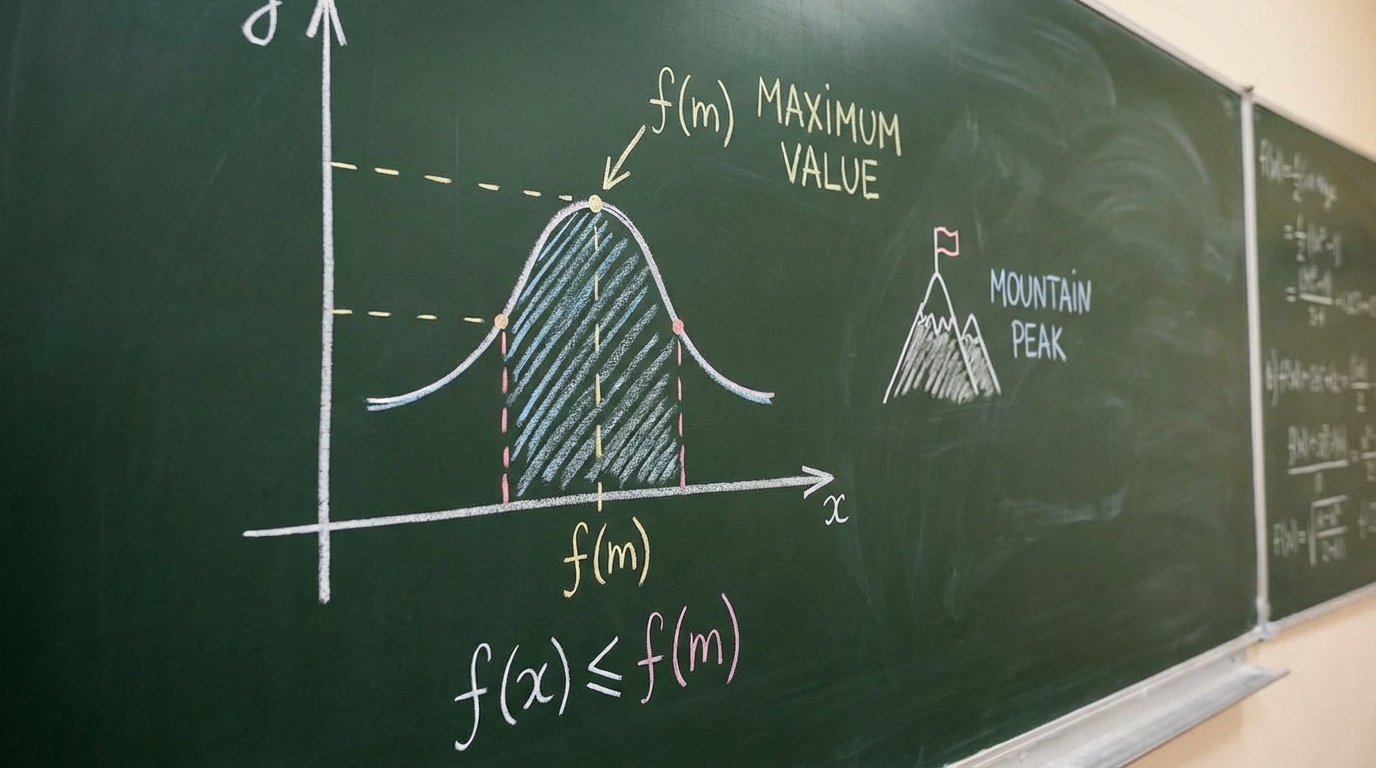
- Maksimum Değeri Bulma: Fonksiyonun maksimum değerini `+3` olarak doğru bir şekilde belirlemiştir. Bu, grafikteki tepe noktasını (maksimum değer) başarıyla tanımlayabildiğini göstermektedir.

Geliştirilmesi Gereken Yönler
- Artan Aralıkları Belirleme ve Aralık Gösterimi: Öğrencinin en belirgin eksiği, artan aralıkları belirlerken uç noktaların aralığa dahil edilip edilmeyeceği konusundadır. İlk soruda artan aralıkları `(-5,-2) U (0,3)` olarak açık aralık (parantez) ile göstermiştir. Doğru cevap `[-5, -2] ∪ [0, 3]` şeklinde kapalı aralık (köşeli parantez) olmalıydı. Bu durum, aralık gösteriminin temellerinde veya bir fonksiyonun uç noktalarda da artan/azalan olabileceği bilgisinde bir eksiklik olduğuna işaret etmektedir.

Ders Dışı Yorumlar
- Ders dışı herhangi bir soru veya yorum kaydedilmemiştir.

📜 Oturum Detayları

06:48:39
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:48:41
💭 AI Öğretmen
Preparing detailed explanation
06:48:41
Görsel
Görsel
06:48:43
AI Öğretmen
Graphs in mathematics are always read from left to right, just like reading a sentence in English.
06:48:45
AI Öğretmen
This way of looking at graphs helps us understand what a function is doing as we move along the x-axis.
06:48:46
AI Öğretmen
When we compare two x-values, we start at the smaller value on the left and go to the bigger value on the right.
06:48:47
AI Öğretmen
Moving from left to right helps us see if the function goes up or down between those two points.
06:48:48
AI Öğretmen
Remembering to read graphs from left to right makes it easier to find and describe when a function is increasing or decreasing.
06:48:49
AI Öğretmen
Did you understand how reading graphs from left to right helps determine if a function is increasing or decreasing?
06:49:17
Öğrenci
I got it
06:49:20
💭 AI Öğretmen
Let us continue now
06:49:21
🎥 Video
06:49:22
AI Öğretmen
Did you understand how to identify an increasing interval of a function?
06:50:00
Öğrenci
I got it
06:50:02
💭 AI Öğretmen
Let us proceed now
06:50:02
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_33e16c0c-dc3a-47bd-91c9-e1d47eecd95c.png) Example: The graph of f is shown on the below. Find the intervals of x for which f(x) is **increasing**.
06:51:43
Öğrenci
My answer is: (-5,-2) U (0,3)
06:51:43
💭 AI Öğretmen
Let me review that answer
06:51:49
AI Öğretmen
Your answer was not correct, let me explain why.
06:51:51
AI Öğretmen
When we talk about where a function is increasing, we look at the parts of the graph where the y-values go up as x increases, and we also check if the endpoints are included by seeing if the function is increasing right at those points.
06:51:52
AI Öğretmen
In this problem, the graph starts increasing at x = -5 and continues up to x = -2, including both endpoints because the function is rising at those exact points. Similarly, it increases again from x = 0 to x = 3, including those points as well.
06:51:55
AI Öğretmen
You used open intervals (-5, -2) and (0, 3), which means you excluded the endpoints, but here the function is increasing at those endpoints, so we use closed intervals [-5, -2] and [0, 3].
06:51:57
AI Öğretmen
For example, if a function rises from x = 1 to x = 4 and also at x = 1 and x = 4 the function is increasing, we write the interval as [1, 4], not (1, 4).
06:51:59
AI Öğretmen
Therefore, the correct answer should be the closed intervals: [-5, -2] ∪ [0, 3].
06:51:59
AI Öğretmen
Should we continue with the lecture?
06:53:08
Öğrenci
Alright, let's continue
06:53:09
💭 AI Öğretmen
Moving forward now
06:53:18
Görsel
Görsel
06:53:21
AI Öğretmen
A function is called decreasing on an interval if, whenever you pick two numbers $x_1$ and $x_2$ in that interval with $x_1$ smaller than $x_2$, the value of the function at $x_1$ is bigger than at $x_2$.
06:53:22
AI Öğretmen
You can picture this like walking down a hill: as you go forward, your height gets lower.
06:53:24
AI Öğretmen
Think about your phone's battery during the day—as more time passes, the amount of battery left goes down, which is an example of a decreasing function.
06:53:25
AI Öğretmen
Does this explanation about decreasing functions make sense to you?
06:53:59
Öğrenci
I got it
06:54:01
💭 AI Öğretmen
Let's review this carefully
06:54:01
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_fb69fa74-e294-4d91-a021-e549025bd3c4.png) Example: The graph of $f$ is shown on the above. Find the intervals of $x$ for which $f(x)$ is **decreasing**.
06:56:58
Öğrenci
My answer is: [-2,0]
06:57:00
💭 AI Öğretmen
Let me review that answer
06:57:04
AI Öğretmen
That's absolutely correct! Fantastic job identifying the interval where the function is decreasing.
06:57:05
AI Öğretmen
You correctly observed that the graph moves downwards from left to right within the interval of x from -2 to 0.
06:57:06
AI Öğretmen
This shows you understand how to interpret a function's behavior directly from its graph, which is a super important skill!
06:57:07
AI Öğretmen
Keep up the great work!
06:57:08
AI Öğretmen
Therefore, the correct answer is [-2, 0].
06:57:08
AI Öğretmen
Should we continue with the lecture?
06:57:37
Öğrenci
Alright, let's continue
06:57:37
💭 AI Öğretmen
Moving forward now
06:57:42
Görsel
Görsel
06:57:44
AI Öğretmen
The maximum value of a function means the biggest output the function has within a certain range or interval.
06:57:47
AI Öğretmen
We write this using math symbols: $f(m)$ is the maximum if, no matter which $x$ you pick in the interval, $f(x)$ is always less than or equal to $f(m)$.
06:57:48
AI Öğretmen
This is called the absolute maximum for that interval, which just means the highest value in that specific part of the function.
06:57:49
AI Öğretmen
If you look at the graph of the function, the maximum is shown at the very top point, like the peak of a mountain.
06:57:49
AI Öğretmen
At this top point, the function does not keep increasing; instead, it stops going up and starts to go down.
06:57:51
AI Öğretmen
There are some functions that do not have a maximum value in every interval, but when it does exist, it looks like the top of a mountain on the graph.
06:57:52
AI Öğretmen
Did this explanation help you understand what a maximum value of a function is?
06:58:35
Öğrenci
I got it
06:58:37
💭 AI Öğretmen
Let us proceed thoughtfully
06:58:37
❓ Soru basic
**Example:** The graph of $g$ is shown below. Find the intervals of $x$ for which $g(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?** ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_11a805a3-b66d-431d-99b4-450c738ea61d.png)
07:05:57
Öğrenci
My answer is: constant: [-2,1] increasing:[-∞,-2] U [1,3] decreasing: [3,∞] the maximum value of this function is +3
07:05:59
💭 AI Öğretmen
Noted your answer
07:06:04
AI Öğretmen
Fantastic job! You've correctly identified the maximum value of the function.
07:06:05
AI Öğretmen
You're absolutely right that the maximum value is +3 because that's the highest point the graph reaches on the y-axis.
07:06:07
AI Öğretmen
It's great that you understand how to find the maximum value by looking for the highest y-coordinate on the graph!
07:06:09
AI Öğretmen
Therefore, the maximum value of this function is 3.
07:06:09
AI Öğretmen
Should we continue with the lecture?

Voltran Okul Analiz Sistemi