← Ana Rapor / Christopher Bora BLAKE / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:28
Bitiş
02 December 2025, 06:47
Süre
19 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
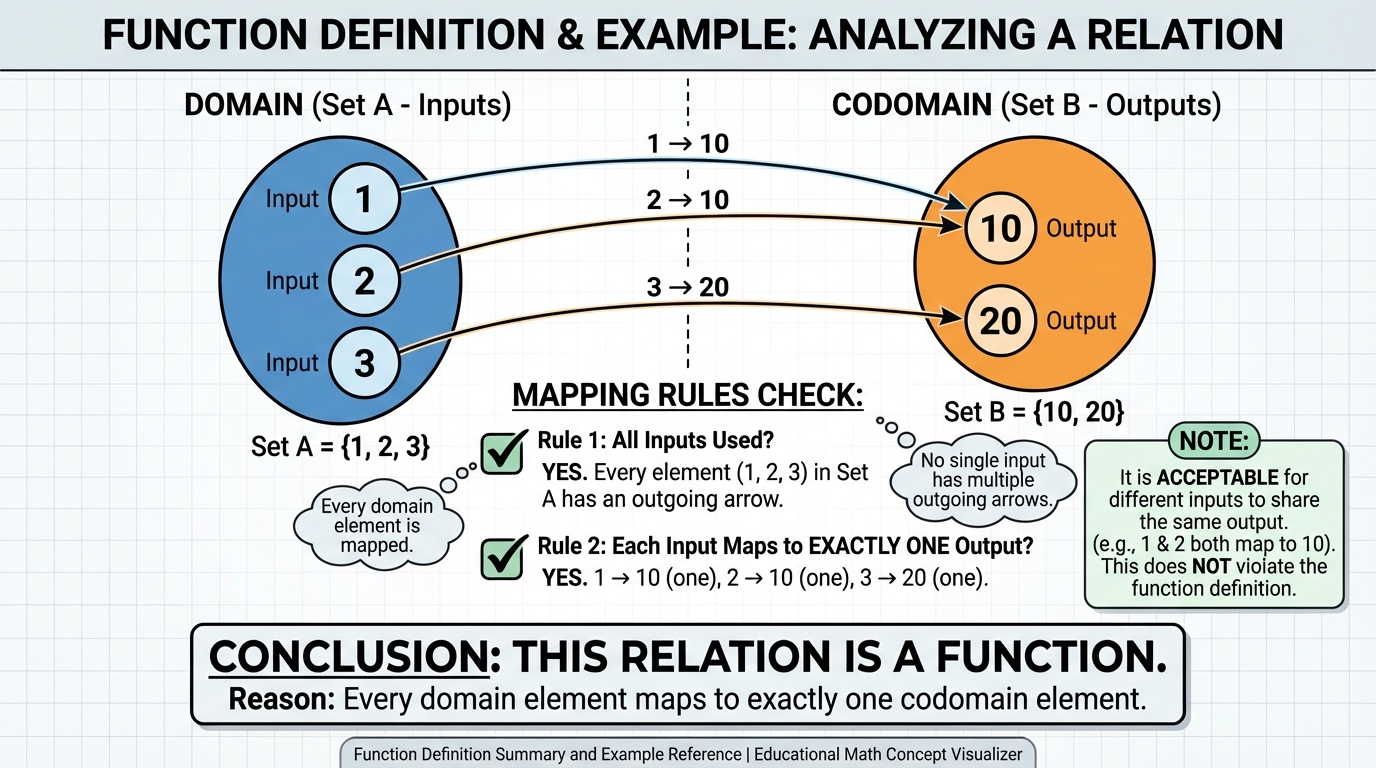
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Öğrenci Performans Analizi

Bu derste öğrencinin "Fonksiyonlar ve Doğrusal Fonksiyonlara Giriş" konusundaki temel kavramları anlama düzeyi değerlendirilmiştir. Öğrenci, dersin genelinde konuya ilgili ve katılımcı bir tutum sergilemiştir. Bazı temel kavramları doğru anlarken, spesifik bir alanda belirgin bir kavram yanılgısı göstermiştir.

# Başarılı Olduğu Konular
Öğrenci, fonksiyon tanımının temel mantığını, tanım ve değer kümelerinin fonksiyon olup olmama durumunu nasıl etkilediğini ve fonksiyonlarda değer bulmayı başarılı bir şekilde kavramıştır.
* Fonksiyon Tanımı: Bir ifadenin fonksiyon olabilmesi için tanım kümesindeki her elemanın değer kümesinde yalnızca bir karşılığı olması gerektiğini doğru bir şekilde anlamıştır. Özellikle, doğal sayılardan doğal sayılara tanımlı olmayan `f(x) = x - 3` fonksiyonu hakkındaki soruyu doğru bir mantıkla açıklamıştır.
* Tanım Kümesi Bulma: Rasyonel bir fonksiyonun en geniş tanım kümesini bulma sorusunda, paydayı sıfır yapan değeri bularak doğru cevaba ulaşmıştır. Bu, fonksiyonların tanım aralıkları üzerindeki kısıtlamaları anladığını göstermektedir.
* Fonksiyonda Değer Bulma: `f(x-1)` şeklinde verilen bir fonksiyonda `f(3)` değerini bulma sorusunu doğru çözmüştür. Bu, fonksiyonel ifadelerle işlem yapma becerisinin yerinde olduğunu göstermektedir.

# Geliştirilmesi Gereken Konular
Öğrencinin en belirgin eksikliği, bir fonksiyonun temel bileşenlerinden biri olan "Görüntü Kümesi" (Range) kavramını anlamada ortaya çıkmıştır.
* Tanım, Değer ve Görüntü Kümesi Ayrımı: Dersteki ilk soruda, şema ile verilen bir fonksiyonun tanım ve değer kümelerini doğru bir şekilde belirlemesine rağmen, görüntü kümesini yanlış tespit etmiştir. Görüntü kümesine, tanım kümesinden elemanlar ve değer kümesinde eşleşmemiş elemanlar dahil etmiştir. Bu durum, görüntü kümesinin "tanım kümesindeki elemanların eşleştiği gerçek çıktılar" olduğu bilgisinin tam olarak oturmadığını göstermektedir. Bu konunun tekrar edilmesi ve pekiştirilmesi gerekmektedir.

# Ders Dışı Yorumlar
Öğrencinin ders dışı herhangi bir yorumu veya sorusu olmamıştır.

📜 Oturum Detayları

06:28:19
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:28:19
💭 AI Öğretmen
Let me prepare that for you
06:28:19
🎥 Video
06:28:21
AI Öğretmen
Did you understand how a function relates elements from Set A to Set B?
06:29:14
Öğrenci
I got it
06:29:17
💭 AI Öğretmen
Let's continue then
06:29:17
🎥 Video
06:29:18
AI Öğretmen
Did the explanation about domain, codomain, and range make sense to you?
06:29:55
Öğrenci
I got it
06:29:57
💭 AI Öğretmen
Let us proceed further
06:29:57
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:31:50
Öğrenci
My answer is: domain:-1,0,1,2 codomain:0,1,2,3,4,5 range:-1,0,1,2,4
06:31:50
💭 AI Öğretmen
Reviewing your response now
06:31:55
AI Öğretmen
Your answer was not correct, let me explain why the range you gave is incorrect.
06:31:58
AI Öğretmen
The domain is the set of all inputs, which you identified correctly as \{-1, 0, 1, 2\}. The codomain is all possible outputs, which you also got right as \{0, 1, 2, 3, 4, 5\}.
06:32:01
AI Öğretmen
The range, however, is the set of actual outputs that the function maps to, not all inputs or unrelated numbers. From the arrows, the outputs are 1 (from -1), 0 (from 0), and 4 (from 1 and 2). So the range is \{0, 1, 4\}.
06:32:04
AI Öğretmen
A common mistake is including elements from the domain or the codomain that are not actual outputs of the function; the range only includes values that the function actually hits. For example, 2 is in the codomain but no input maps to it, so it’s not in the range.
06:32:07
AI Öğretmen
Therefore, the correct answer should be: Domain: \{-1, 0, 1, 2\}, Codomain: \{0, 1, 2, 3, 4, 5\}, Range: \{0, 1, 4\}.
06:32:07
AI Öğretmen
Should we continue with the lecture?
06:33:15
Öğrenci
Alright, let's continue
06:33:15
💭 AI Öğretmen
Moving forward now
06:33:23
Görsel
Görsel
06:33:26
AI Öğretmen
A relation is called a function if it follows a special rule.
06:33:27
AI Öğretmen
This rule says that every input, which is each element from the Domain (also called Set A), must be paired with one output in the Codomain (Set B).
06:33:29
AI Öğretmen
It is important to remember that not every element in the Codomain has to be used, so some elements in Set B can be left without a match.
06:33:31
AI Öğretmen
Also, it is allowed for different inputs (from Set A) to have the same output (in Set B); this is called many-to-one mapping.
06:33:32
AI Öğretmen
However, it is not allowed for one input to be linked to more than one output; in other words, one-to-many mappings are not allowed.
06:33:33
AI Öğretmen
So, a function connects every input from the Domain to exactly one output in the Codomain.
06:33:34
AI Öğretmen
Does this explanation make the concept of a function clear to you?
06:34:14
Öğrenci
I got it
06:34:17
💭 AI Öğretmen
Let us proceed carefully
06:34:17
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:36:39
Öğrenci
My answer is: it isnt a function because the number needs to be zero or above to be natural.
06:36:40
💭 AI Öğretmen
Let me review that carefully
06:36:45
AI Öğretmen
That's absolutely right! Fantastic job!
06:36:48
AI Öğretmen
You correctly identified that for $f(x) = x - 3$ to be a function from $\mathbb{N}$ to $\mathbb{N}$, every input from the natural numbers must result in an output that is also a natural number.
06:36:50
AI Öğretmen
When you pick natural numbers like 1 or 2, $f(1) = -2$ and $f(2) = -1$, which are not natural numbers.
06:36:51
AI Öğretmen
This shows you understand the importance of the domain and codomain in defining a function!
06:36:51
AI Öğretmen
Should we continue with the lecture?
06:37:21
Öğrenci
Alright, let's continue
06:37:22
💭 AI Öğretmen
Moving forward now
06:37:32
Görsel
Görsel
06:37:35
AI Öğretmen
A relation connects each item in one set to items in another set, and we can check if it’s a function by following certain rules.
06:37:36
AI Öğretmen
Let's look at two sets: Set A is our input set, it has the numbers 1, 2, and 3. Set B is the output set, which contains 10 and 20.
06:37:39
AI Öğretmen
Here is how the mapping works: 1 is paired with 10, 2 is paired with 10, and 3 is paired with 20.
06:37:42
AI Öğretmen
When we check the mappings, we see that every input—1, 2, and 3—has been matched. None are left out, and none is matched with more than one output.
06:37:43
AI Öğretmen
It’s also okay if two inputs go to the same output. For example, both 1 and 2 go to 10, and this still follows the rule for functions.
06:37:44
AI Öğretmen
Therefore, this relation is a function, because every input from Set A goes to exactly one output in Set B.
06:37:45
AI Öğretmen
Did you understand why this relation is considered a function?
06:38:29
Öğrenci
I got it
06:38:31
💭 AI Öğretmen
Let us review this closely
06:38:31
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:41:07
Öğrenci
My answer is: all real numbers -2
06:41:09
💭 AI Öğretmen
Let me review that answer
06:41:12
AI Öğretmen
That's absolutely correct! Fantastic job!
06:41:14
AI Öğretmen
You correctly identified that the denominator of a fraction cannot be zero, which is the key restriction for rational functions like this one.
06:41:16
AI Öğretmen
By setting $x+2 \neq 0$, you found the exact value that needs to be excluded from the domain.
06:41:18
AI Öğretmen
This shows a great understanding of how to find the domain of functions with denominators!
06:41:20
AI Öğretmen
Therefore, the correct answer is all real numbers except -2.
06:41:20
AI Öğretmen
Should we continue with the lecture?
06:41:40
Öğrenci
Alright, let's continue
06:41:42
💭 AI Öğretmen
Moving on now
06:41:52
AI Öğretmen
A relation is called a function if every input value in the domain is paired with only one output value in the codomain.
06:41:52
AI Öğretmen
This means, each input matches with just one output, but it is okay if two or more different inputs have the same output.
06:41:53
AI Öğretmen
Does the idea of a function having exactly one output for each input make sense to you?
06:42:16
Öğrenci
I got it
06:42:18
💭 AI Öğretmen
Let us review this.
06:42:19
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:44:30
Öğrenci
My answer is: 18
06:44:31
💭 AI Öğretmen
Noted your answer
06:44:36
AI Öğretmen
Fantastic job! You've correctly identified that $f(3) = 18$.
06:44:38
AI Öğretmen
You brilliantly set the expression inside the function, $(x - 1)$, equal to 3 to find the correct $x$-value.
06:44:40
AI Öğretmen
Then, you substituted that $x$-value back into the function's rule to get the final answer.
06:44:41
AI Öğretmen
This shows a great understanding of function evaluation!
06:44:42
AI Öğretmen
Therefore the correct answer is 18.
06:44:42
AI Öğretmen
Should we continue with the lecture?
06:45:05
Öğrenci
Alright, let's continue
06:45:06
💭 AI Öğretmen
Moving forward now
06:45:15
AI Öğretmen
In this lesson, we covered the definition of a function as a special type of relation where each input from the domain maps to exactly one output in the codomain. We also discussed the concepts of domain, codomain, and range, and how to determine if a relation is a function by checking these mappings. Additionally, we looked at examples to identify domain, codomain, and range, and understood that multiple inputs can share the same output, but one input cannot have multiple outputs. Do you have any questions about these topics? If not, I’ll end the lesson here.
06:47:02
Öğrenci
wrap upb
06:47:07
AI Öğretmen
See you in the next lesson!

Voltran Okul Analiz Sistemi