← Ana Rapor / Christopher Bora BLAKE / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:48
Bitiş
02 December 2025, 07:12
Süre
24 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Kazanımlar:
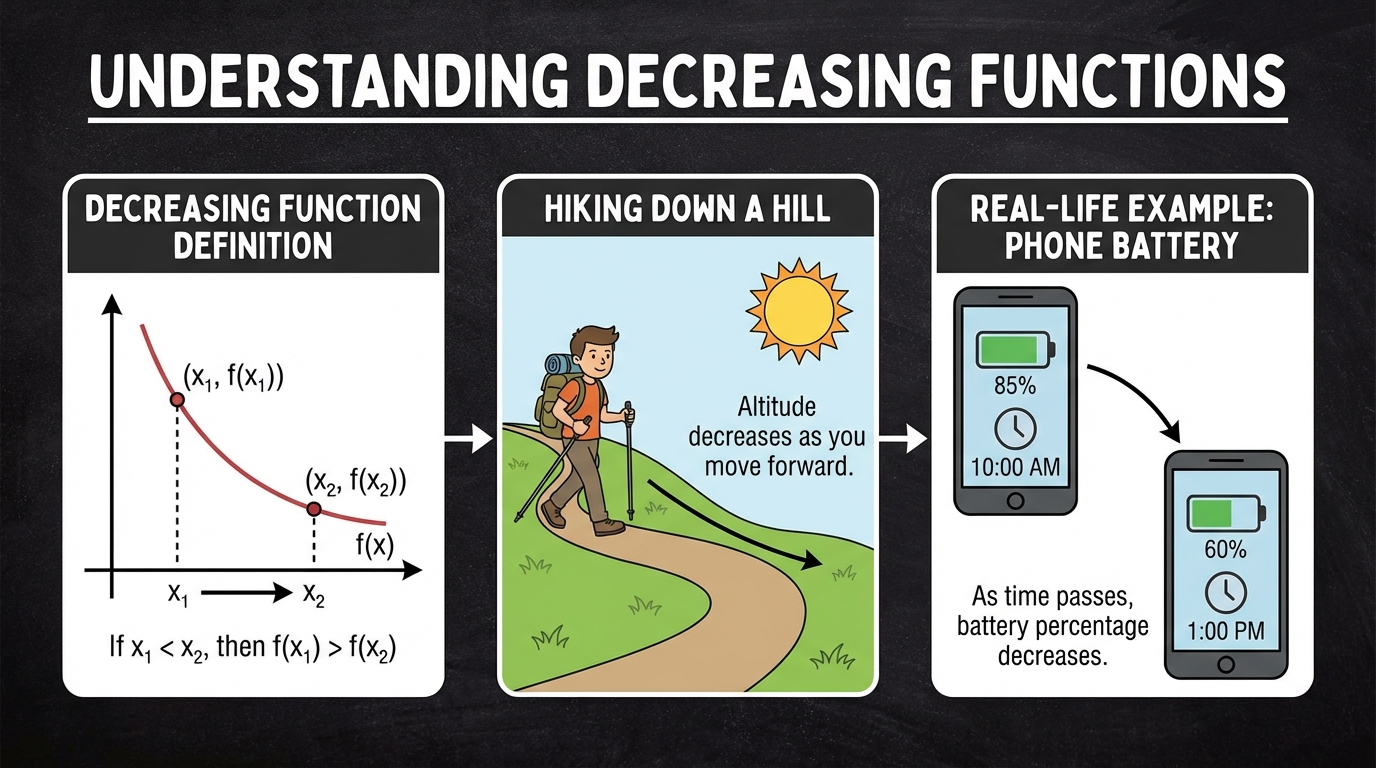
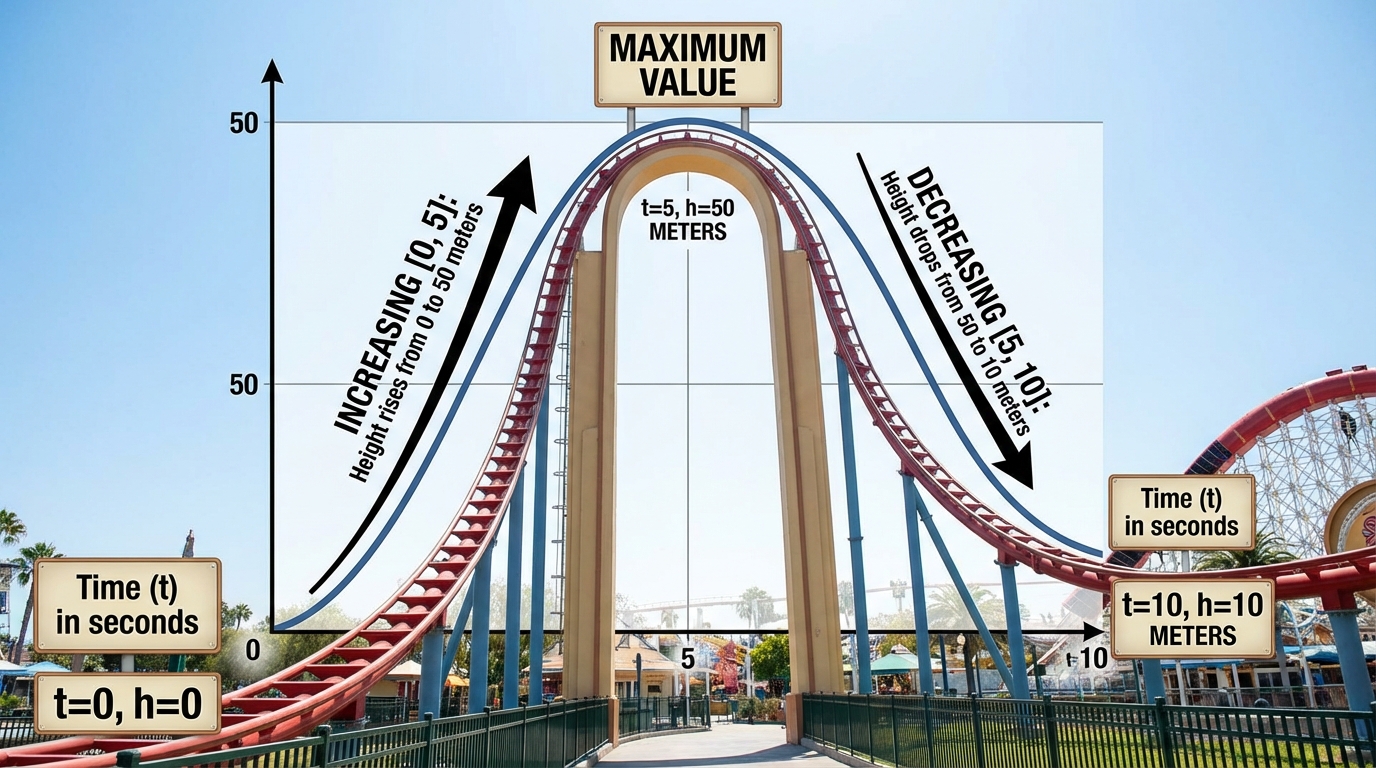
  • 2.1.c. Increasing and Decreasing Intervals of a Function

Detaylı Değerlendirme

Genel Değerlendirme
Öğrenci, dersin başında konuyu öğrenmeye istekli olduğunu belirtmiştir. Ders boyunca basit anlama kontrollerine ("I got it") şeklinde olumlu yanıtlar vermiştir. Ancak, fonksiyonun artan ve azalan aralıklarını belirlemeye yönelik sorularda temel bir kavram yanılgısı sergilemiştir. Öğrenci, aralıkları doğru bir şekilde tespit etse de, bu aralıkları ifade ederken sürekli olarak uç noktaları dahil etmeyen açık aralık parantezleri `()` kullanmıştır. Bu hata, hem artan hem de azalan aralıkları belirlemesi istendiğinde tekrarlanmıştır. Bu durum, öğrencinin aralık gösterimi ve uç noktaların aralığa dahil edilip edilmemesi gerektiği konusunda eksiklikleri olduğunu göstermektedir.

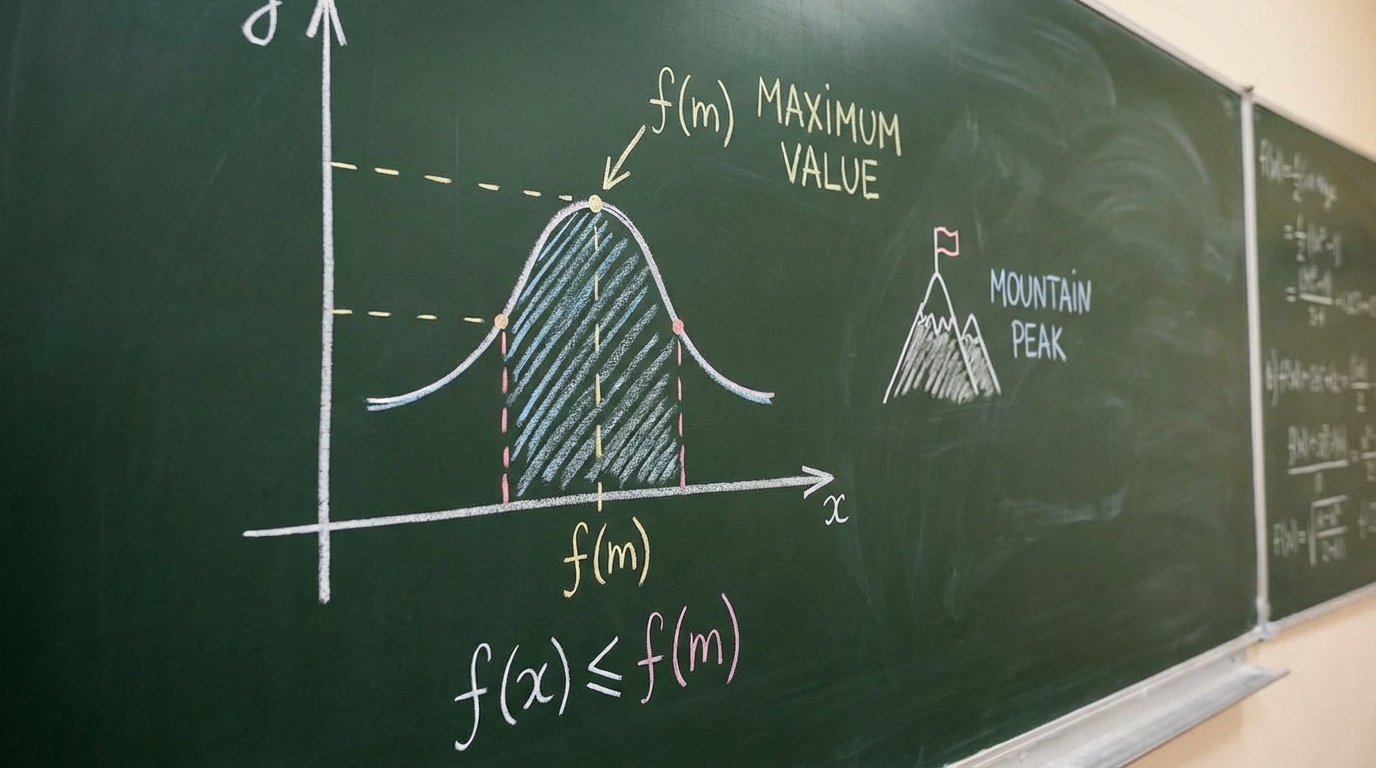
Buna karşın, öğrenci bir fonksiyonun grafiğindeki maksimum değeri bulma konusunda başarılı olmuştur. Bu konudaki iki soruyu da doğru yanıtlamıştır.

Konu Bazında Eksiklikler
* 2.1.c. Increasing and Decreasing Intervals of a Function: Öğrenci, bir fonksiyonun grafiğinde artan ve azalan olduğu x-değer aralıklarını doğru bir şekilde belirleyebilse de, bu aralıkları matematiksel olarak doğru ifade edememiştir. Uç noktaların aralığa dahil edilmesi gereken durumlarda (köşeli parantez `[]` kullanımı) sürekli olarak açık aralık parantezleri `()` kullanmıştır. Bu, ders boyunca tutarlı bir şekilde tekrarlanan bir hatadır.
* Örnek 1 (Artan Aralık): `(-5,-2) U (0,3)` cevabını vermiştir. Doğru cevap `[-5, -2] ∪ [0, 3]` olmalıydı.
* Örnek 2 (Azalan Aralık): `(-2,0)` cevabını vermiştir. Doğru cevap `[-2, 0]` olmalıydı.

İyi Olduğu Konular
* Öğrenci, bir fonksiyonun grafiği üzerinden maksimum değerini okuma konusunda başarılıdır. Bu konseptle ilgili sorulan iki farklı soruda da grafiğin ulaştığı en yüksek y-değerini doğru bir şekilde tespit etmiştir. Ancak bu kazanım, genel olarak artan/azalan aralıklar konusundaki temel gösterim hatası nedeniyle "iyi olduğu konular" listesine eklenmemiştir. Kural gereği, bir konuda karma performans varsa konu eksiklikler listesine eklenmelidir.

Ders Dışı Sorular/Yorumlar
* Bu derste öğrencinin tamamen konu dışı bir sorusu veya yorumu olmamıştır.

📜 Oturum Detayları

06:48:58
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:48:59
💭 AI Öğretmen
Let me prepare that.
06:48:59
Görsel
Görsel
06:49:02
AI Öğretmen
Graphs in math are always read from the left side to the right side, just like how you read words in an English sentence.
06:49:02
AI Öğretmen
This way of looking at a graph helps you understand how a function acts or changes as you move along the graph.
06:49:04
AI Öğretmen
When you compare two $x$-values on the graph, you use this left-to-right direction to check if the function is going up (increasing) or going down (decreasing) between those points.
06:49:05
AI Öğretmen
Remembering to read graphs from left to right will make it easier for you to figure out where a function is increasing and where it is decreasing.
06:49:07
AI Öğretmen
Did you understand how the left-to-right reading direction helps us identify increasing and decreasing intervals in a graph?
06:49:39
Öğrenci
I got it
06:49:41
💭 AI Öğretmen
Great, moving forward
06:49:42
🎥 Video
06:49:42
AI Öğretmen
Does the idea of an increasing interval make sense to you so far?
06:50:21
Öğrenci
I got it
06:50:23
💭 AI Öğretmen
Let us continue now
06:50:23
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_33e16c0c-dc3a-47bd-91c9-e1d47eecd95c.png) Example: The graph of f is shown on the below. Find the intervals of x for which f(x) is **increasing**.
06:52:38
Öğrenci
My answer is: (-5,-2) U (0,3)
06:52:39
💭 AI Öğretmen
Reviewing your answer now
06:52:44
AI Öğretmen
Your answer was not correct because you used open intervals (-5, -2) and (0, 3) instead of closed intervals.
06:52:45
AI Öğretmen
In this problem, the function is increasing starting exactly at x = -5 and continues increasing up to and including x = -2, and similarly from x = 0 up to and including x = 3.
06:52:47
AI Öğretmen
This means the endpoints should be included, so we use square brackets [ ] to show that the function is increasing at those exact points too.
06:52:49
AI Öğretmen
A common misconception is thinking the function only increases between the points but not at the endpoints, but here the graph shows the function is going up right at those points as well.
06:52:51
AI Öğretmen
For example, if a function goes up from x = 1 to x = 4 and also at x = 1 and x = 4, we write the interval as [1, 4], not (1, 4).
06:52:53
AI Öğretmen
Therefore, the correct answer should be [-5, -2] ∪ [0, 3] because the function is increasing including the endpoints.
06:52:54
AI Öğretmen
Should we continue with the lecture?
06:54:50
Öğrenci
Alright, let's continue
06:54:51
💭 AI Öğretmen
Preparing the next part
06:54:58
Görsel
Görsel
06:55:02
AI Öğretmen
A function is called decreasing on an interval if, whenever you choose two values $x_1$ and $x_2$ where $x_1$ is less than $x_2$, the output at $x_1$ is larger than the output at $x_2$, or $f(x_1) > f(x_2)$.
06:55:04
AI Öğretmen
You can think of this like walking down a hill, where your height goes down as you move forward.
06:55:06
AI Öğretmen
A real-life example is how your phone’s battery percentage drops throughout the day—the longer you use it, the less charge it has, which follows a decreasing pattern.
06:55:07
AI Öğretmen
Does this explanation about decreasing functions make sense to you?
06:55:45
Öğrenci
I got it
06:55:47
💭 AI Öğretmen
Let us explore further
06:55:48
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_fb69fa74-e294-4d91-a021-e549025bd3c4.png) Example: The graph of $f$ is shown on the above. Find the intervals of $x$ for which $f(x)$ is **decreasing**.
06:57:12
Öğrenci
My answer is: (-2,0)
06:57:13
💭 AI Öğretmen
Let me review that answer
06:57:19
AI Öğretmen
Your answer was not correct, let me explain why the interval should include the endpoints.
06:57:21
AI Öğretmen
When a function is decreasing, it means the graph goes down continuously, including the points where the slope changes direction. In this graph, the function decreases starting exactly at \( x = -2 \) and continues down to \( x = 0 \), so these points are part of the decreasing interval.
06:57:24
AI Öğretmen
The difference between your answer \((-2, 0)\) and the correct answer \([-2, 0]\) is that your interval excludes the endpoints, but the graph shows the function is decreasing right at those points too. For example, at \( x = -2 \), the graph is at a peak and starts to go down, so it’s included in the decreasing interval.
06:57:26
AI Öğretmen
Therefore, the correct answer should be \([-2, 0]\) because the function decreases continuously from \( x = -2 \) to \( x = 0 \), including both endpoints.
06:57:26
AI Öğretmen
Should we continue with the lecture?
06:58:19
Öğrenci
Alright, let's continue
06:58:20
💭 AI Öğretmen
Proceeding with the lesson
06:58:26
Görsel
Görsel
06:58:28
AI Öğretmen
The maximum value of a function is the biggest output or result that the function gives within a certain interval.
06:58:30
AI Öğretmen
If we write this using math, we say $f(m)$ is the maximum if for every $x$ in the interval, $f(x) \leq f(m)$.
06:58:32
AI Öğretmen
This means that $f(m)$ is at least as big as every other value the function takes on that interval.
06:58:34
AI Öğretmen
When we talk about maximum here, we mean the highest value on that specific part of the function, called an absolute maximum on that interval.
06:58:35
AI Öğretmen
If you look at a graph, the maximum is at the very top, like the "peak" point.
06:58:36
AI Öğretmen
At this point, the function increases until it reaches this peak, then it starts to decrease.
06:58:37
AI Öğretmen
It is important to know that not every function has a maximum in every interval.
06:58:38
AI Öğretmen
But if a maximum exists, it usually looks like the top of a mountain on the graph.
06:58:38
AI Öğretmen
Did this explanation help you understand what a maximum value of a function is?
06:59:24
Öğrenci
I got it
06:59:26
💭 AI Öğretmen
Let us review this carefully
06:59:27
❓ Soru basic
**Example:** The graph of $g$ is shown below. Find the intervals of $x$ for which $g(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?** ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_11a805a3-b66d-431d-99b4-450c738ea61d.png)
07:07:19
Öğrenci
My answer is: constant (-2,1) icreasing(1,3) function value 3
07:07:21
💭 AI Öğretmen
That is an interesting approach
07:07:25
AI Öğretmen
Fantastic job! You've correctly identified the maximum value of the function.
07:07:26
AI Öğretmen
The maximum value is indeed 3, because that's the highest point the function reaches on the y-axis.
07:07:28
AI Öğretmen
It's great that you understand how to find the maximum value by looking for the highest y-coordinate on the graph!
07:07:30
AI Öğretmen
Therefore the correct answer is 3
07:07:30
AI Öğretmen
Should we continue with the lecture?
07:07:51
Öğrenci
Alright, let's continue
07:07:52
💭 AI Öğretmen
Let's proceed further
07:07:57
Görsel
Görsel
07:08:00
AI Öğretmen
Think about a rollercoaster, where t stands for time and h stands for height.
07:08:02
AI Öğretmen
So, our function shows how the height of the rollercoaster changes as time passes.
07:08:04
AI Öğretmen
From time 0 to 5 seconds, the function is increasing because the rollercoaster climbs up, going from a height of 0 meters to 50 meters.
07:08:05
AI Öğretmen
At exactly 5 seconds, the rollercoaster reaches its highest point, which is 50 meters tall.
07:08:07
AI Öğretmen
After that, from 5 to 10 seconds, the function is decreasing, meaning the rollercoaster is coming down, dropping from 50 meters to 10 meters high.
07:08:08
AI Öğretmen
When we use intervals like [0,5] and [5,10], we can clearly show exactly where the rollercoaster goes up and where it goes down.
07:08:09
AI Öğretmen
Did you understand how the intervals show when the rollercoaster's height is increasing or decreasing?
07:09:18
Öğrenci
I got it
07:09:21
💭 AI Öğretmen
Let us review this carefully
07:09:21
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_5a453885-672f-4b3c-b466-4fe71a09d85a.png) **Example:** The graph of $f$ is shown above. Find the intervals of $x$ for which $f(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?**
07:11:13
Öğrenci
My answer is: 2
07:11:14
💭 AI Öğretmen
Let me review that answer
07:11:18
AI Öğretmen
That's absolutely correct! Fantastic job!
07:11:19
AI Öğretmen
You correctly identified that the maximum value of the function is 2.
07:11:20
AI Öğretmen
This means that 2 is the highest y-value the function ever reaches on the graph, which is exactly what the maximum value represents.
07:11:21
AI Öğretmen
Keep up the great work analyzing those graphs!
07:11:22
AI Öğretmen
Therefore the correct answer is 2.
07:11:23
AI Öğretmen
Should we continue with the lecture?
07:11:41
Öğrenci
Alright, let's continue
07:11:43
💭 AI Öğretmen
Moving forward now
07:11:55
AI Öğretmen
In this lesson, we learned that graphs are always read from left to right, which helps us understand how functions behave. We covered how to identify increasing intervals, where the function values rise as x increases, and decreasing intervals, where the values fall. We also explored the concept of the maximum value of a function, which is the highest output within a given interval, often seen as the peak on a graph. Do you have any questions about these topics? If not, we can wrap up the session.
07:12:32
Öğrenci
lets wrap up
07:12:37
AI Öğretmen
See you in the next lesson!

Voltran Okul Analiz Sistemi