← Ana Rapor / Özge Irmak REKA / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:28
Bitiş
Devam ediyor
Süre
13 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, dersin başında konunun detaylı bir şekilde anlatılmasını istese de, ders boyunca sorulan tüm sorulara doğru ve eksiksiz cevaplar vermiştir. Bu durum, öğrencinin konuyu hızlı bir şekilde kavradığını ve temel kavramları başarıyla uygulayabildiğini göstermektedir. Performansı oldukça başarılıdır.

Detaylı Analiz

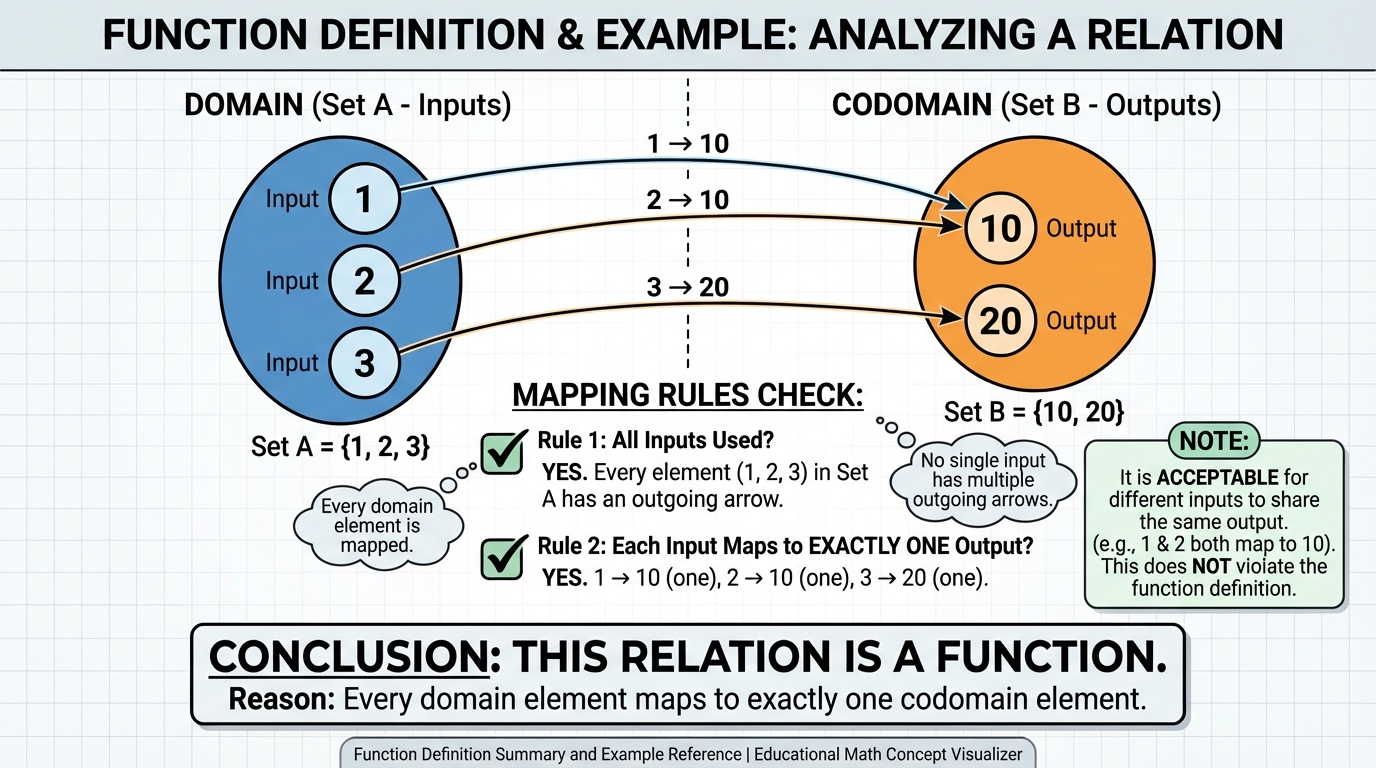
- Fonksiyon Tanımı ve Temel Kavramlar: Öğrenci, bir fonksiyonun tanım kümesi, değer kümesi ve görüntü kümesi arasındaki ilişkiyi doğru bir şekilde belirleyebilmiştir. Verilen bir fonksiyonda bu kümeleri hatasız bir şekilde bulmuştur.
- Bir Bağıntının Fonksiyon Olma Şartı: Öğrenci, bir bağıntının hangi koşullarda fonksiyon olarak tanımlanabileceğini anlamıştır. Özellikle, tanım kümesindeki bir elemanın değer kümesi dışında bir elemanla eşleşmesi durumunda bunun bir fonksiyon olmayacağını doğru bir şekilde açıklamıştır.
- Fonksiyon Değeri Bulma: Tanım kümesinde yapılan değişikliklere (örneğin, f(x-1) gibi) rağmen, istenen fonksiyon değerini (f(3) gibi) bulmak için doğru adımları izlemiş ve işlemi hatasız tamamlamıştır.
- En Geniş Tanım Kümesi: Rasyonel bir fonksiyonun paydasını sıfır yapan değeri bularak en geniş tanım kümesini doğru bir şekilde ifade etmiştir.

Sonuç

Öğrenci, "Formal Definitions of Functions" alt konusuyla ilgili tüm temel kazanımlara hakim görünüyor. Ders boyunca herhangi bir kavram yanılgısı veya eksiklik gözlemlenmemiştir. Öğrencinin konuya olan hakimiyeti yüksektir.

📜 Oturum Detayları

06:28:57
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:28:58
💭 AI Öğretmen
Preparing detailed explanation
06:28:58
🎥 Video
06:28:59
AI Öğretmen
Did you understand how a function relates elements from one set to another?
06:30:43
Öğrenci
I got it
06:30:45
💭 AI Öğretmen
Let's continue forward
06:30:46
🎥 Video
06:30:46
AI Öğretmen
Did you understand how the domain, codomain, and range relate to each other in a function?
06:31:57
Öğrenci
I got it
06:31:59
💭 AI Öğretmen
Let us proceed shortly
06:31:59
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:33:13
Öğrenci
My answer is: Domain: -1,0,1,2 Codomain: 0,1,2,3,4,5 Range: 0,1,4
06:33:14
💭 AI Öğretmen
Reviewing your answer now
06:33:18
AI Öğretmen
Fantastic job! You've absolutely nailed it!
06:33:19
AI Öğretmen
You correctly identified the domain as all the input values in set A, the codomain as all possible output values in set B, and the range as only the values in B that are actually mapped to.
06:33:20
AI Öğretmen
This shows you have a great understanding of these fundamental function concepts! Keep up the amazing work!
06:33:22
AI Öğretmen
Therefore the correct answer is Domain: $\{-1, 0, 1, 2\}$, Codomain: $\{0, 1, 2, 3, 4, 5\}$, Range: $\{0, 1, 4\}$
06:33:22
AI Öğretmen
Should we continue with the lecture?
06:34:25
Öğrenci
Alright, let's continue
06:34:26
💭 AI Öğretmen
Preparing the next part
06:34:35
Görsel
Görsel
06:34:37
AI Öğretmen
A relation is called a function if it follows an important rule.
06:34:38
AI Öğretmen
This rule says: Every input from the domain (also called Set A) must be matched to one output in the codomain (Set B).
06:34:39
AI Öğretmen
It is important to remember, not every output in the codomain (Set B) has to be used. Some outputs might be left over and that is allowed.
06:34:40
AI Öğretmen
More than one input can share the same output. This means different inputs can be matched to the same output.
06:34:41
AI Öğretmen
However, one input cannot be connected to two or more different outputs.
06:34:43
AI Öğretmen
Each input is matched to only one output. That is what makes a relation a function.
06:34:44
AI Öğretmen
A function always assigns exactly one value from the codomain to each element in the domain.
06:34:44
AI Öğretmen
Did the explanation of what makes a relation a function make sense to you?
06:35:39
Öğrenci
I got it
06:35:42
💭 AI Öğretmen
Now let's review this question
06:35:43
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:36:21
Öğrenci
My answer is: This is not a funting on if f(2) them f(2)=-1 which is not a natural number
06:36:21
💭 AI Öğretmen
Let me review that
06:36:27
AI Öğretmen
That's absolutely right! Fantastic job explaining why this relation isn't a function.
06:36:29
AI Öğretmen
You correctly pointed out that for values like $x=2$, the output $f(2)=-1$ is not a natural number, even though the domain is natural numbers.
06:36:32
AI Öğretmen
This shows you understand that for a relation to be a function, every input from the domain must have an output that belongs to the specified codomain. Keep up the great work!
06:36:32
AI Öğretmen
Therefore, the correct answer is No, it is not a function.
06:36:33
AI Öğretmen
Should we continue with the lecture?
06:36:58
Öğrenci
Alright, let's continue
06:36:59
💭 AI Öğretmen
Continuing shortly
06:37:04
Görsel
Görsel
06:37:06
AI Öğretmen
A relation between two sets can be checked to see if it is a function by following certain rules.
06:37:07
AI Öğretmen
Let's look at Set A, which we call the inputs, containing the numbers 1, 2, and 3.
06:37:08
AI Öğretmen
Set B, called the outputs, contains the numbers 10 and 20.
06:37:09
AI Öğretmen
The mappings in this example are 1 maps to 10, 2 maps to 10, and 3 maps to 20.
06:37:10
AI Öğretmen
This means that every input from Set A—1, 2, and 3—has a matching output in Set B.
06:37:13
AI Öğretmen
Also, each input is connected to only one output; 1 goes to 10, 2 goes to 10, and 3 goes to 20.
06:37:15
AI Öğretmen
It's perfectly fine if different inputs share the same output, like 1 and 2 both mapping to 10.
06:37:16
AI Öğretmen
In conclusion, this relationship qualifies as a function because every input in the domain points to exactly one output in the codomain.
06:37:17
AI Öğretmen
Did you understand how to determine if a relation is a function based on the example?
06:38:05
Öğrenci
I got it
06:38:08
💭 AI Öğretmen
Let us proceed now
06:38:08
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:38:26
Öğrenci
My answer is: Domf=R-(-2)
06:38:27
💭 AI Öğretmen
Let me review that answer
06:38:31
AI Öğretmen
That's absolutely correct! Fantastic job!
06:38:32
AI Öğretmen
You correctly identified that the denominator of a fraction cannot be zero, which is the key restriction for rational functions.
06:38:32
AI Öğretmen
This shows you understand how to find the domain by excluding values that would make the expression undefined.
06:38:34
AI Öğretmen
Keep up the great work!
06:38:35
AI Öğretmen
Therefore the correct answer is Domf=R-(-2).
06:38:36
AI Öğretmen
Should we continue with the lecture?
06:39:07
Öğrenci
Alright, let's continue
06:39:08
💭 AI Öğretmen
Preparing the next part
06:39:16
AI Öğretmen
A relation is considered a function when each input value from the domain pairs with only one output value from the codomain.
06:39:17
AI Öğretmen
This means that no single input can link to more than one output, though different inputs can still have the same output.
06:39:19
AI Öğretmen
It is allowed for multiple inputs to share the same output within a function.
06:39:20
AI Öğretmen
As long as each input has exactly one output, the relation qualifies as a function.
06:39:21
AI Öğretmen
Does this explanation about what makes a relation a function make sense to you?
06:39:49
Öğrenci
I got it
06:39:52
💭 AI Öğretmen
Let's reinforce this concept.
06:39:52
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:40:55
Öğrenci
My answer is: x=4 for f(3) so 4x+2=16+2=18 so f(18)
06:40:56
💭 AI Öğretmen
Let me review that
06:41:01
AI Öğretmen
Fantastic job! You correctly figured out that to find $f(3)$, you need to set the expression inside the parentheses, $x-1$, equal to 3.
06:41:03
AI Öğretmen
This led you to the correct value of $x=4$. Then, by substituting $x=4$ into $4x+2$, you accurately calculated the output!
06:41:04
AI Öğretmen
You've shown a great understanding of how to evaluate functions by finding the correct input value first. Keep up the excellent work!
06:41:06
AI Öğretmen
Therefore, the correct answer is 18.
06:41:06
AI Öğretmen
Should we continue with the lecture?
06:41:38
Öğrenci
Alright, let's continue
06:41:39
💭 AI Öğretmen
Moving forward now
06:41:50
AI Öğretmen
In this lesson, we covered what defines a function as a special type of relation where each input in the domain maps to exactly one output in the codomain. We discussed the roles of domain, codomain, and range, and looked at examples to determine whether a relation qualifies as a function. We also practiced finding the domain of a function and evaluating function values. Do you have any questions about these topics? If not, we can wrap up the session.

Voltran Okul Analiz Sistemi