← Ana Rapor / Eren ABUDARAM / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:47
Bitiş
Devam ediyor
Süre
12 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
  • 2.1.c. Increasing and Decreasing Intervals of a Function

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, dersin başında konunun detaylı bir şekilde anlatılmasını isteyerek derse ilgili bir başlangıç yapmıştır. Ancak, ders boyunca AI öğretmenin açıklamalarından sonra sık sık "I got it" (Anladım) demesine rağmen, takip eden sorularda bu konuları tam olarak anlamadığı görülmüştür.

# Analiz

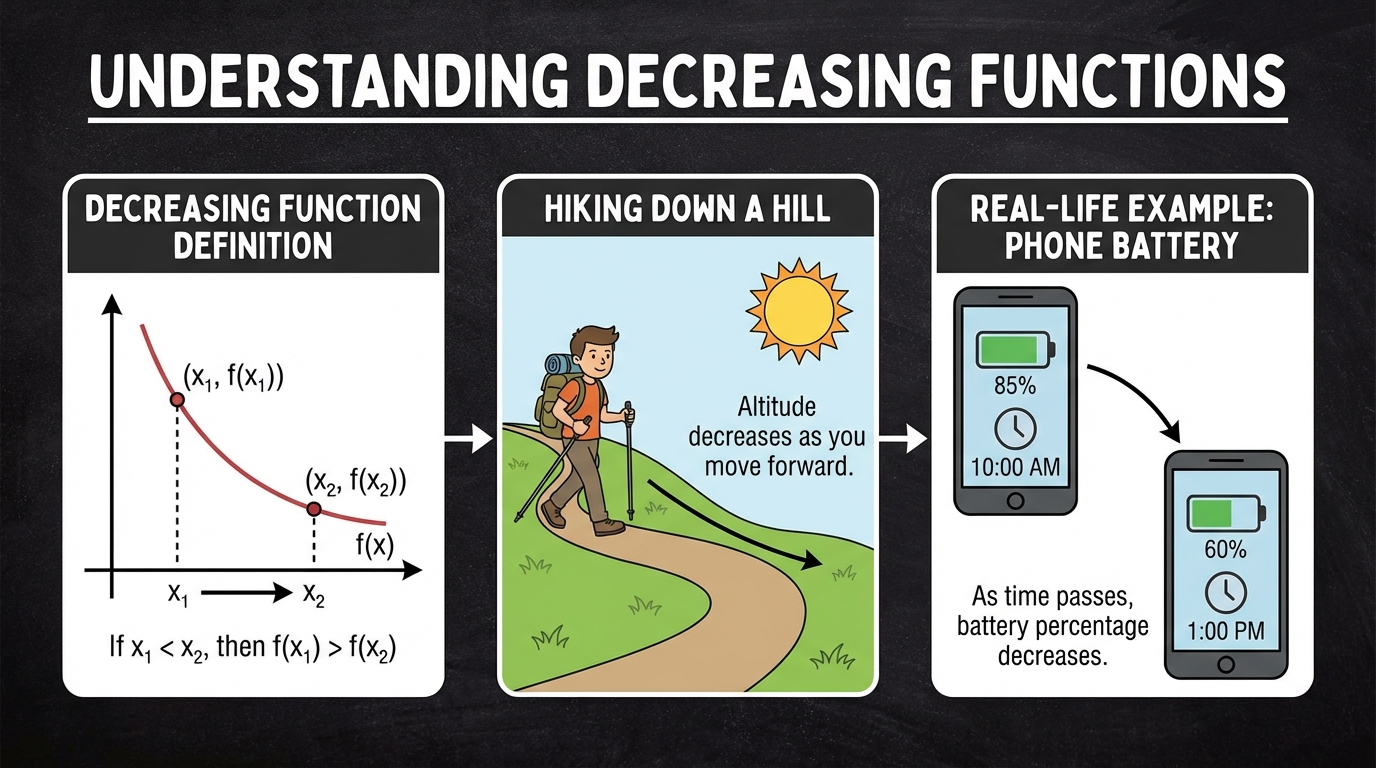
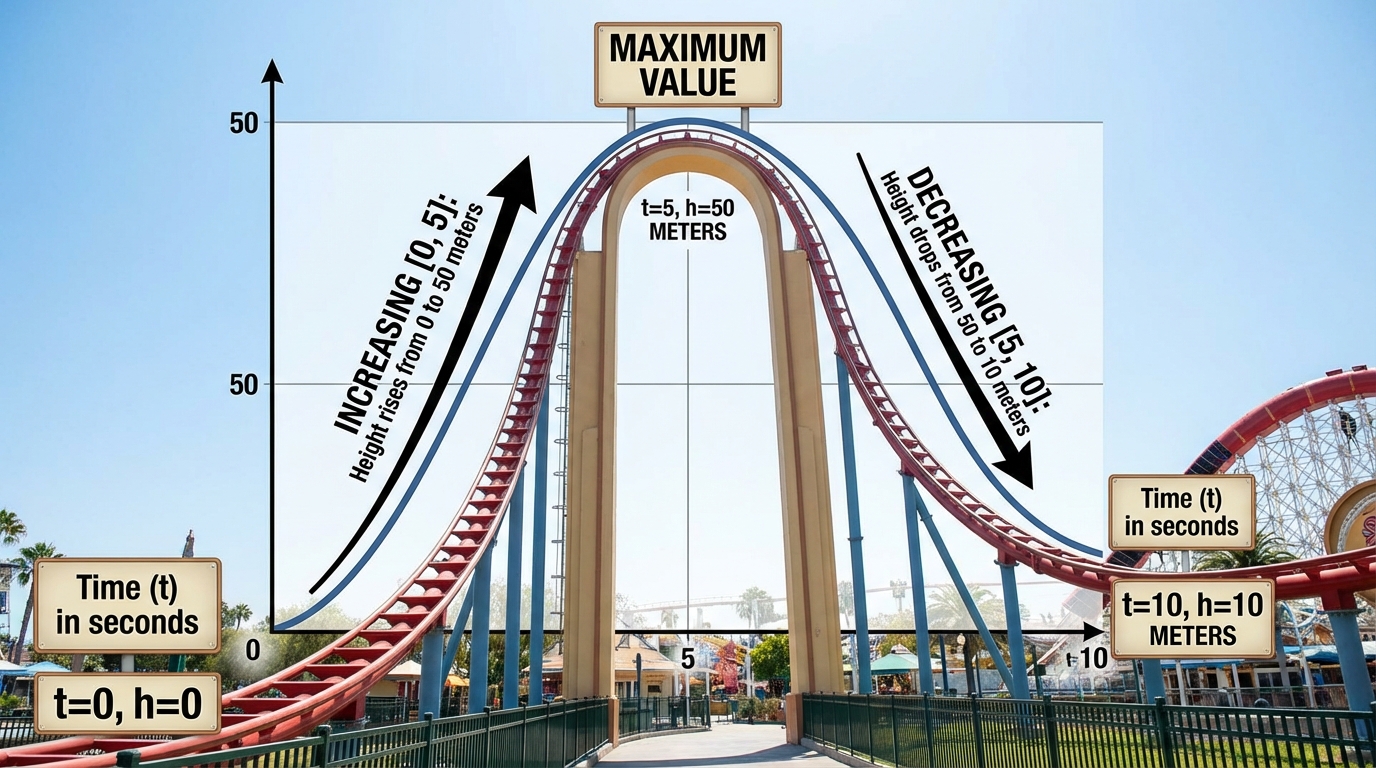
* Artan ve Azalan Aralıklar: Öğrencinin bu konudaki en temel eksiği, aralıkların matematiksel gösterimindedir.
* Artan Aralık Sorusu: Öğrenci, artan aralıkları `(-5 -2)` ve `(0,3)` olarak belirtmiştir. Doğru x-değerlerini bulmasına rağmen, aralıkların kapalı olduğunu belirten köşeli parantez `[]` yerine, açık olduğunu belirten normal parantez `()` kullanmıştır. Bu, fonksiyonun aralığın başlangıç ve bitiş noktalarında da arttığı gerçeğini anlamadığını veya aralık gösterimi kuralını bilmediğini göstermektedir.
* Azalan Aralık Sorusu: Öğrenci, azalan aralığı `(0,-2)` olarak cevaplamıştır. Burada iki temel hata yapmıştır: Birincisi, yine açık aralık parantezi kullanmıştır. İkincisi ve daha önemlisi, bir aralık yazılırken küçük sayının sola, büyük sayının sağa yazılması kuralını ihlal etmiştir. Bu, hem aralık yazım kurallarında hem de grafiği soldan sağa okuma becerisinde eksiklik olduğunu düşündürmektedir.
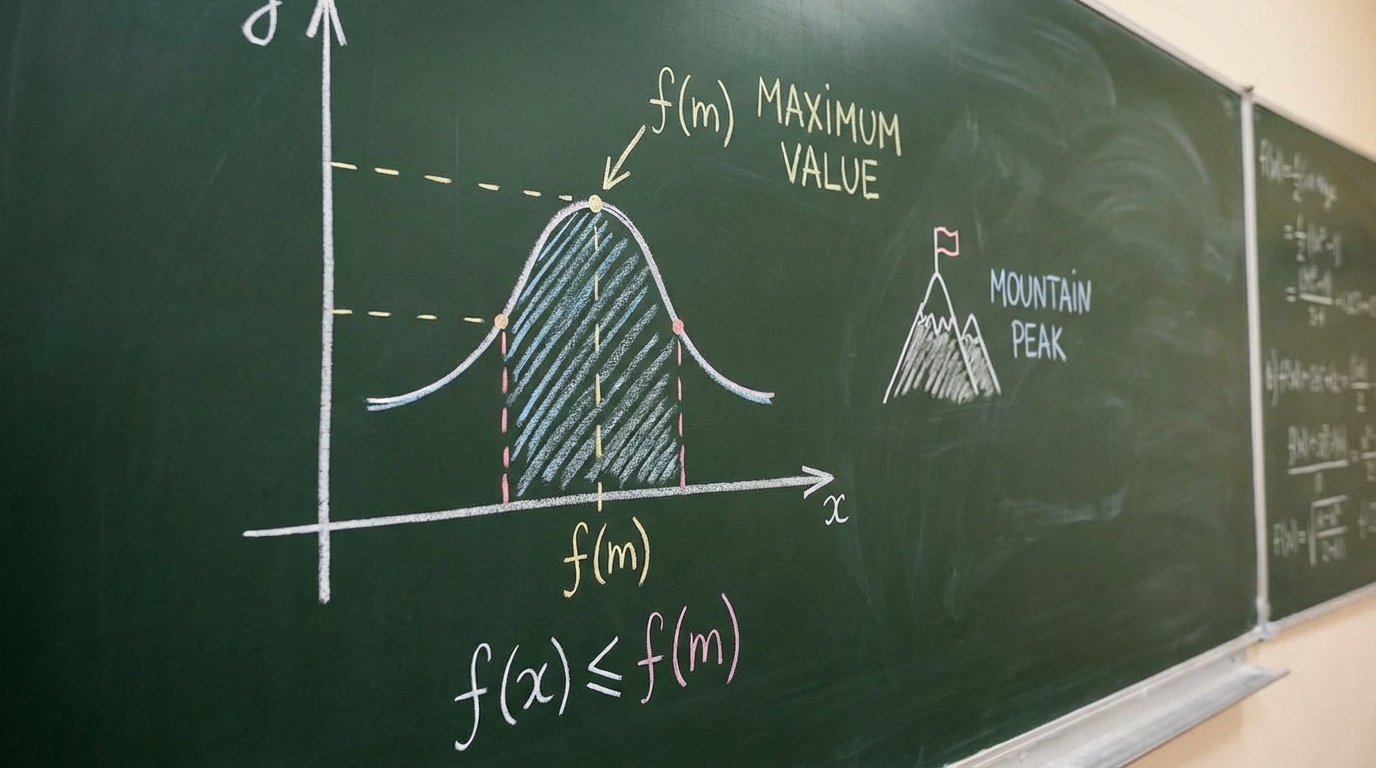
* Maksimum Değer Tespiti: Öğrenci, dersin ilerleyen kısımlarında sorulan ve bir fonksiyonun grafiğindeki maksimum değeri bulmayı gerektiren iki soruyu da (`3` ve `2` cevaplarıyla) doğru yanıtlamıştır. Bu, öğrencinin bir grafiğin en yüksek noktasını (tepe noktasını) görsel olarak tespit etme ve bu noktanın y-eksenindeki değerini okuma becerisine sahip olduğunu göstermektedir.

# Sonuç

Öğrenci, bir fonksiyonun tepe noktası gibi belirgin görsel özelliklerini tanımlayabilmektedir. Ancak, fonksiyonun davranışını (artma/azalma) tanımlayan aralıkları doğru bir şekilde yazma konusunda ciddi eksiklikleri bulunmaktadır. Özellikle aralıkların açık mı kapalı mı olduğu (parantez seçimi) ve aralık yazım sıralaması konularında temel bilgi eksikliği vardır. Bu nedenle, konunun temelini oluşturan aralık gösterimi üzerinde daha fazla durulması gerekmektedir.

📜 Oturum Detayları

06:47:52
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:47:53
💭 AI Öğretmen
Getting the details ready
06:47:53
Görsel
Görsel
06:47:56
AI Öğretmen
Graphs in mathematics are always read from left to right, just like reading a sentence in English.
06:47:57
AI Öğretmen
This is important because it helps us understand how a function changes as the x-values move from smaller to bigger numbers.
06:48:00
AI Öğretmen
When we compare two x-values, we use this left-to-right direction to see if the function is getting higher or lower between those points.
06:48:01
AI Öğretmen
Remembering to look at graphs from left to right makes it easier to find and describe where a function is increasing or decreasing.
06:48:01
AI Öğretmen
Did you understand how reading graphs from left to right helps us identify increasing and decreasing intervals?
06:48:38
Öğrenci
I got it
06:48:41
💭 AI Öğretmen
Very well understood
06:48:42
🎥 Video
06:48:42
AI Öğretmen
Did you understand how an increasing interval is defined and what it represents on a graph?
06:49:26
Öğrenci
I got it
06:49:29
💭 AI Öğretmen
Let us review this part
06:49:29
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_33e16c0c-dc3a-47bd-91c9-e1d47eecd95c.png) Example: The graph of f is shown on the below. Find the intervals of x for which f(x) is **increasing**.
06:50:14
Öğrenci
My answer is: (-5 -2) (0,3)
06:50:15
💭 AI Öğretmen
Let me review that answer
06:50:22
AI Öğretmen
Your answer was not correct, let me explain why the correct intervals include the endpoints.
06:50:24
AI Öğretmen
When a function is increasing on an interval, it means the y-values go up as x moves from left to right, and this includes the points where the increase starts or stops, which are the endpoints.
06:50:26
AI Öğretmen
In this graph, the function starts increasing exactly at x = -5 and continues up to x = -2, including both points because the y-values at these points show the function rising. The same applies to the interval from x = 0 to x = 3.
06:50:27
AI Öğretmen
A common misconception is thinking increasing intervals always use open parentheses, but if the function is increasing right at those endpoints, we use square brackets to include them.
06:50:30
AI Öğretmen
For example, if a graph rises steadily from x = 1 to x = 4, including the points at 1 and 4 where the rise starts and ends, the interval is written as [1, 4], not (1, 4).
06:50:31
AI Öğretmen
Therefore, the correct answer should be the union of the intervals including endpoints: [-5, -2] ∪ [0, 3].
06:50:32
AI Öğretmen
Should we continue with the lecture?
06:51:28
Öğrenci
Alright, let's continue
06:51:29
💭 AI Öğretmen
Proceeding with the lecture
06:51:36
Görsel
Görsel
06:51:40
AI Öğretmen
A function is called decreasing on an interval when, every time you choose two numbers from that interval, where the first one is smaller than the second one, the function’s value at the first number is bigger than its value at the second number.
06:51:43
AI Öğretmen
In other words, if you pick $x_1$ and $x_2$ from the interval and $x_1$ is less than $x_2$, then $f(x_1)$ will be greater than $f(x_2)$.
06:51:45
AI Öğretmen
You can picture this like walking down a hill—each step you take forward, your height goes down.
06:51:46
AI Öğretmen
A simple real-life example is your phone’s battery level: as time moves forward during the day, the percentage of battery usually goes down, just like a decreasing function.
06:51:47
AI Öğretmen
Does the idea of a function decreasing on an interval make sense to you so far?
06:52:38
Öğrenci
I got it
06:52:40
💭 AI Öğretmen
Let's reinforce this idea
06:52:41
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_fb69fa74-e294-4d91-a021-e549025bd3c4.png) Example: The graph of $f$ is shown on the above. Find the intervals of $x$ for which $f(x)$ is **decreasing**.
06:53:00
Öğrenci
My answer is: (0,-2)
06:53:01
💭 AI Öğretmen
Thank you for sharing
06:53:08
AI Öğretmen
Your answer was not correct, let me explain why. The interval you gave, (0, -2), is written in reverse order, and intervals should be written with the smaller number first.
06:53:09
AI Öğretmen
Also, the function is decreasing where the graph goes down as you move from left to right. Looking at the graph, the function decreases from \( x = -2 \) to \( x = 0 \), not from 0 to -2.
06:53:10
AI Öğretmen
Remember, when writing intervals, the left endpoint should be less than the right endpoint, and use square brackets if the endpoints are included. So, the correct interval where \( f(x) \) is decreasing is \([-2, 0]\).
06:53:12
AI Öğretmen
Therefore, the correct answer should be \([-2, 0]\).
06:53:12
AI Öğretmen
Should we continue with the lecture?
06:54:00
Öğrenci
Alright, let's continue
06:54:02
💭 AI Öğretmen
Proceeding to next section
06:54:08
Görsel
Görsel
06:54:11
AI Öğretmen
The maximum value of a function is the biggest output a function gives within a certain part of its graph, which we call an interval.
06:54:12
AI Öğretmen
We say $f(m)$ is the maximum if for every $x$ in that interval, the function’s value at $x$ is less than or equal to $f(m)$.
06:54:14
AI Öğretmen
This is the exact definition for the highest value that a function reaches in that specific part of its domain, also called the absolute maximum on the interval.
06:54:16
AI Öğretmen
If you look at the graph of a function, the maximum is seen at the very highest point or "peak", which is where the graph stops going up and starts going down.
06:54:17
AI Öğretmen
Some functions may not have a maximum in every interval, but when they do, the highest point looks just like the top of a mountain.
06:54:17
AI Öğretmen
Do you feel clear about what a maximum value of a function means within an interval?
06:55:01
Öğrenci
I got it
06:55:04
💭 AI Öğretmen
Now let's check understanding
06:55:04
❓ Soru basic
**Example:** The graph of $g$ is shown below. Find the intervals of $x$ for which $g(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?** ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_11a805a3-b66d-431d-99b4-450c738ea61d.png)
06:56:08
Öğrenci
My answer is: 3
06:56:08
💭 AI Öğretmen
Good, noting your answer
06:56:13
AI Öğretmen
That's absolutely correct! Fantastic job!
06:56:14
AI Öğretmen
You correctly identified that the maximum value of the function is 3.
06:56:15
AI Öğretmen
This is because the maximum value is the highest y-coordinate the function reaches on the entire graph.
06:56:16
AI Öğretmen
You clearly understand how to find the peak of a function from its graph! Keep up the great work!
06:56:17
AI Öğretmen
Therefore the correct answer is 3.
06:56:17
AI Öğretmen
Should we continue with the lecture?
06:56:53
Öğrenci
Alright, let's continue
06:56:54
💭 AI Öğretmen
Moving to new concept
06:57:00
Görsel
Görsel
06:57:01
AI Öğretmen
Imagine a rollercoaster where t stands for time and h stands for height.
06:57:02
AI Öğretmen
The function we are looking at tells us how the height of the rollercoaster changes as time passes.
06:57:04
AI Öğretmen
From time t equals 0 to t equals 5, the height goes up from 0 meters to 50 meters.
06:57:06
AI Öğretmen
This means the function is increasing on the interval from 0 to 5 seconds, or $[0,5]$.
06:57:08
AI Öğretmen
At t equals 5 seconds, the rollercoaster reaches its highest point, which is 50 meters.
06:57:09
AI Öğretmen
From t equals 5 to t equals 10 seconds, the height goes down from 50 meters to 10 meters.
06:57:11
AI Öğretmen
So, the function is decreasing on the interval from 5 to 10 seconds, or $[5,10]$.
06:57:13
AI Öğretmen
When we use intervals like $[0,5]$ and $[5,10]$, it helps us clearly show when the rollercoaster is going up or down.
06:57:13
AI Öğretmen
Do you understand how the intervals show when the rollercoaster's height is increasing or decreasing?
06:57:51
Öğrenci
I got it
06:57:54
💭 AI Öğretmen
Let us review this carefully
06:57:54
❓ Soru basic
![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_5a453885-672f-4b3c-b466-4fe71a09d85a.png) **Example:** The graph of $f$ is shown above. Find the intervals of $x$ for which $f(x)$ is **a)** constant **b)** increasing **c)** decreasing **What is the maximum value of the function?**
06:58:59
Öğrenci
My answer is: 2
06:59:00
💭 AI Öğretmen
Let me review that answer
06:59:04
AI Öğretmen
Fantastic job! You are absolutely correct!
06:59:05
AI Öğretmen
The maximum value of a function is the highest y-value it reaches on its graph.
06:59:07
AI Öğretmen
You correctly identified that the highest point on this graph corresponds to a y-value of 2.
06:59:08
AI Öğretmen
Keep up the great work analyzing graphs!
06:59:09
AI Öğretmen
Therefore the correct answer is 2.
06:59:09
AI Öğretmen
Should we continue with the lecture?
06:59:39
Öğrenci
Alright, let's continue
06:59:40
💭 AI Öğretmen
Moving forward now
06:59:49
AI Öğretmen
In this lesson, we learned how to read graphs from left to right to understand a function's behavior, identified increasing and decreasing intervals by comparing function values at different x-values, and explored the concept of maximum values as the highest points on a graph. Do you have any questions about these topics? If not, we can wrap up the lesson here.

Voltran Okul Analiz Sistemi