← Ana Rapor / Eren ABUDARAM / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:31
Bitiş
Devam ediyor
Süre
14 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
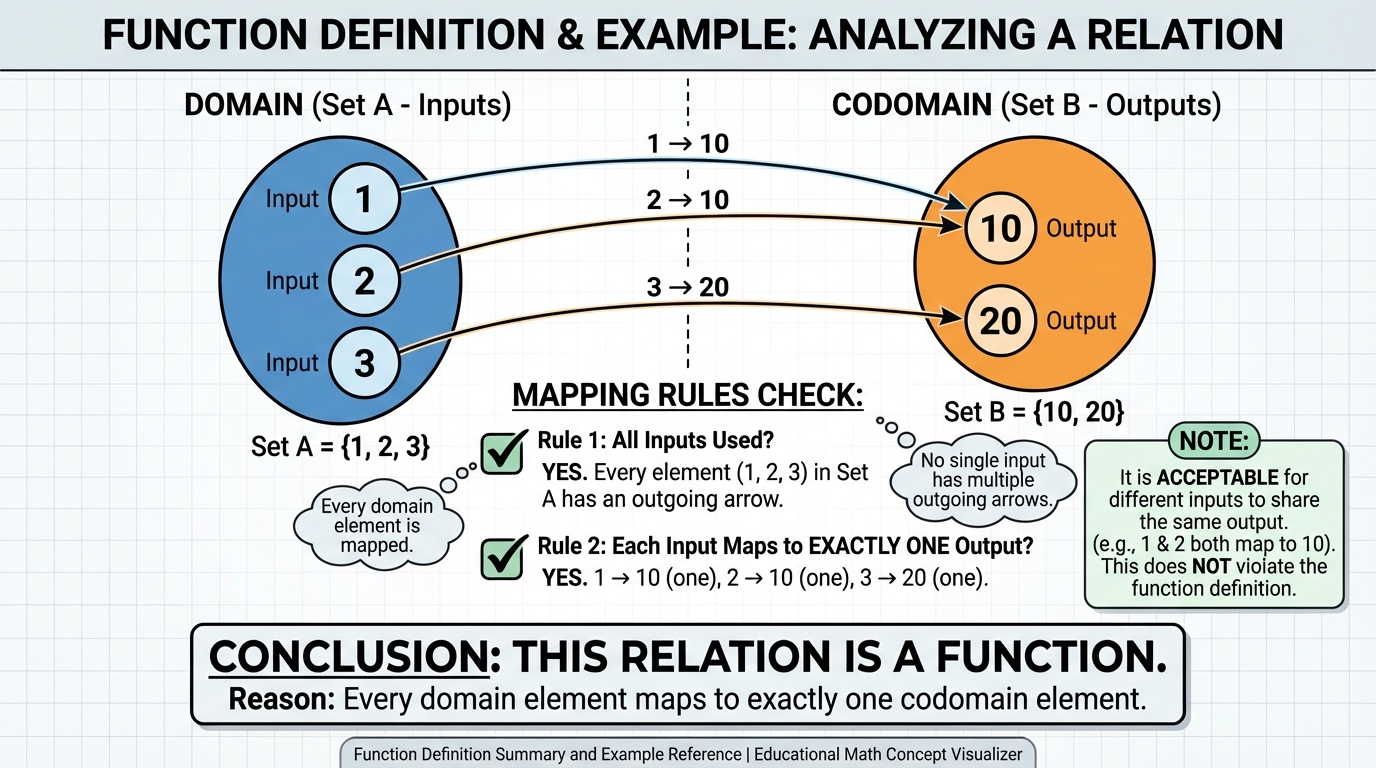
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Öğrenci Performans Analizi

Bu derste öğrencinin fonksiyonların temel tanımları konusundaki performansı analiz edilmiştir. Öğrencinin konuya ilgisi olsa da temel kavramlarda önemli eksiklikleri olduğu gözlemlenmiştir.

# Genel Değerlendirme
Öğrenci, bazı işlemsel adımları doğru bir şekilde uygulayabilmektedir. Örneğin, bir rasyonel fonksiyonun tanım kümesini bulma (paydayı sıfır yapan değeri çıkarma) ve verilen bir değer için fonksiyonu hesaplama (değer yerine koyma) gibi konularda başarılı olmuştur.

Ancak, fonksiyonun temel tanımı ve ilgili kavramlar (görüntü kümesi, tanım kümesi, değer kümesi ilişkisi) konusunda ciddi kafa karışıklığı yaşamaktadır. Özellikle bir bağıntının fonksiyon olup olmadığını belirleme ve görüntü kümesini doğru tespit etme gibi temel konularda yanlış cevaplar vermiştir. Bu durum, öğrencinin konunun mantığını tam olarak kavramadığını, daha çok ezbere dayalı veya işlemsel adımları takip ettiğini göstermektedir.

# Gözlemlenen Eksiklikler
* Görüntü Kümesi (Range) Kavramı: Öğrenci, kendisine sorulan ilk soruda tanım kümesi (domain) ve değer kümesini (codomain) doğru bir şekilde belirlemiş, ancak görüntü kümesini (range) tanım kümesi ile karıştırmıştır. Görüntü kümesinin, tanım kümesindeki elemanların fonksiyon altındaki "gerçek" çıktıları olduğu bilgisini kavrayamamıştır.
* Fonksiyon Olma Şartı: Öğrenci, bir bağıntının fonksiyon olup olmadığını belirleme konusunda zorlanmıştır. Özellikle, bir fonksiyonun çıktılarının (görüntü kümesi) mutlaka değer kümesinin (codomain) bir alt kümesi olması gerektiği kuralını gözden kaçırmıştır. Doğal sayılardan doğal sayılara tanımlı `f(x) = x - 3` bağıntısının bir fonksiyon olduğunu düşünmesi, bu konudaki en belirgin eksiğidir. Çünkü `x=1` için `f(1)=-2` olur ve `-2` bir doğal sayı değildir, yani değer kümesinde yer almaz.

# İyi Olduğu Konular
* Rasyonel Fonksiyonların Tanım Kümesi: Öğrenci, paydalı bir fonksiyonun tanım kümesini bulurken paydayı sıfır yapan değeri tanım kümesinden çıkarması gerektiğini doğru bir şekilde tespit etmiştir.
* Fonksiyonda Değer Bulma: `f(x-1) = 4x + 2` verildiğinde `f(3)` değerini bulma sorusunu doğru yanıtlamıştır. Bu, fonksiyonel denklemlerde doğru `x` değerini bularak yerine koyma becerisine sahip olduğunu göstermektedir.

Sonuç olarak öğrencinin, fonksiyonların işlemsel kısımlarında daha başarılı olduğu ancak temel tanım ve kavramsal anlayışta desteğe ihtiyacı olduğu görülmektedir.

📜 Oturum Detayları

06:31:51
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:31:52
💭 AI Öğretmen
Preparing detailed explanation
06:31:52
🎥 Video
06:31:53
AI Öğretmen
Did you understand how a function relates elements from Set A to Set B?
06:32:55
Öğrenci
I got it
06:32:57
💭 AI Öğretmen
Let us continue then
06:32:58
🎥 Video
06:32:59
AI Öğretmen
Did you understand how the domain, codomain, and range relate to each other in a function?
06:33:37
Öğrenci
I got it
06:33:39
💭 AI Öğretmen
Let us proceed now
06:33:39
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:35:29
Öğrenci
My answer is: domain:-1,0,1,2 codomain:0,1,2,3,4,5 range:-1,0,1,2
06:35:30
💭 AI Öğretmen
Let me review that answer
06:35:35
AI Öğretmen
Your answer was not correct, let me explain why the range you gave is wrong.
06:35:37
AI Öğretmen
The range is the set of actual output values that the function maps to from the domain, not the domain elements themselves. You listed domain values (-1, 0, 1, 2) as the range, which is a common mix-up.
06:35:39
AI Öğretmen
To find the range, look at the arrows from each domain element and note where they point in the codomain: - -1 maps to 1 - 0 maps to 0 - 1 maps to 4 - 2 maps to 4 So the range is {0, 1, 4}, the actual outputs of the function.
06:35:42
AI Öğretmen
For example, if a function maps inputs {a, b, c} to outputs {2, 3, 3}, the range would be {2, 3}, not the input set.
06:35:43
AI Öğretmen
Therefore, the correct answers should be: Domain: {-1, 0, 1, 2} Codomain: {0, 1, 2, 3, 4, 5} Range: {0, 1, 4}
06:35:44
AI Öğretmen
Should we continue with the lecture?
06:36:36
Öğrenci
Alright, let's continue
06:36:37
💭 AI Öğretmen
Proceeding to next section
06:36:43
Görsel
Görsel
06:36:46
AI Öğretmen
A relation is called a function if it follows one important rule.
06:36:48
AI Öğretmen
Every input, which is each element from the Domain (this is also called Set A), should be connected to some output in the Codomain (this is Set B).
06:36:50
AI Öğretmen
Not every element in the Codomain has to be matched to an input, so it is okay if there are extra elements in Set B that do not get chosen.
06:36:52
AI Öğretmen
It is also allowed for different inputs from Set A to have the same output in Set B, so it is fine if two or more inputs point to one output.
06:36:53
AI Öğretmen
However, it is not allowed for one input in the Domain to be matched to more than one output in the Codomain at the same time.
06:36:55
AI Öğretmen
This means a function always assigns exactly one output from the Codomain to each input from the Domain.
06:36:56
AI Öğretmen
Did you understand how a relation qualifies as a function based on the input-output rules?
06:37:50
Öğrenci
I got it
06:37:52
💭 AI Öğretmen
Let us proceed now
06:37:53
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:39:22
Öğrenci
My answer is: function
06:39:23
💭 AI Öğretmen
Let me review that answer
06:39:27
AI Öğretmen
Your answer was not correct, let me explain why.
06:39:29
AI Öğretmen
The relation \( f : \mathbb{N} \to \mathbb{N} \) defined by \( f(x) = x - 3 \) is supposed to assign a natural number to every natural number input.
06:39:31
AI Öğretmen
However, if you try \( x = 1 \), then \( f(1) = 1 - 3 = -2 \), which is not a natural number because natural numbers are positive integers starting from 1.
06:39:32
AI Öğretmen
Since the output is not in the codomain \( \mathbb{N} \) for some inputs, this relation does not meet the definition of a function from \( \mathbb{N} \) to \( \mathbb{N} \).
06:39:33
AI Öğretmen
A common misconception is thinking any rule that assigns one output per input is a function, but the output must also belong to the codomain specified.
06:39:35
AI Öğretmen
For example, if \( f: \mathbb{N} \to \mathbb{Z} \) (integers) and \( f(x) = x - 3 \), then it would be a function because integers include negative numbers.
06:39:36
AI Öğretmen
Therefore, the correct answer should be: No, it is not a function.
06:39:36
AI Öğretmen
Should we continue with the lecture?
06:41:05
Öğrenci
Alright, let's continue
06:41:06
💭 AI Öğretmen
Proceeding with lecture
06:41:13
Görsel
Görsel
06:41:15
AI Öğretmen
A relation is a way of connecting elements from one set to elements in another set.
06:41:16
AI Öğretmen
To see if a relation is a function, we need to follow some special rules.
06:41:17
AI Öğretmen
Imagine we have two sets called Set A and Set B.
06:41:18
AI Öğretmen
Set A is our group of inputs, and it has the numbers 1, 2, and 3.
06:41:19
AI Öğretmen
Set B is our group of possible outputs, and it has the numbers 10 and 20.
06:41:21
AI Öğretmen
We have three connections: 1 is linked to 10, 2 is linked to 10, and 3 is linked to 20.
06:41:23
AI Öğretmen
That means for every number in Set A, there is a matching number in Set B.
06:41:24
AI Öğretmen
It is okay if more than one input matches to the same output, like 1 and 2 both matching with 10.
06:41:25
AI Öğretmen
What matters is that each input goes to only one output, not two different ones.
06:41:26
AI Öğretmen
Since every input from Set A is used, and each one connects to just one output in Set B, this is a function.
06:41:28
AI Öğretmen
So, the rule for being a function is: every input matches with only one output, and it is okay if different inputs share the same output.
06:41:29
AI Öğretmen
Do you understand why this relation qualifies as a function?
06:42:27
Öğrenci
I got it
06:42:30
💭 AI Öğretmen
Let's reinforce this concept
06:42:30
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:42:46
Öğrenci
My answer is: r-(-2=
06:42:47
💭 AI Öğretmen
Let me review that answer
06:42:51
AI Öğretmen
That's absolutely right! You've correctly identified that the value of x that makes the denominator zero must be excluded from the domain.
06:42:53
AI Öğretmen
Great job remembering that division by zero is undefined, which is a crucial concept for finding the domain of rational functions.
06:42:55
AI Öğretmen
This means the function is defined for all real numbers except when x equals -2.
06:42:57
AI Öğretmen
Therefore, the correct answer is $\{x \in \mathbb{R} \mid x \neq -2\}$.
06:42:57
AI Öğretmen
Should we continue with the lecture?
06:43:32
Öğrenci
Alright, let's continue
06:43:33
💭 AI Öğretmen
Moving forward now
06:43:40
AI Öğretmen
A relation is a function if every input value from the domain connects to one and only one output value in the codomain.
06:43:42
AI Öğretmen
This means that for any number you pick from the domain set, you should find only one result in the codomain, not more than one.
06:43:43
AI Öğretmen
Different inputs from the domain can still lead to the same output in the codomain, and this is allowed in functions.
06:43:45
AI Öğretmen
But each input must not have two or more different outputs.
06:43:46
AI Öğretmen
Only one output is connected to each input in a function.
06:43:47
AI Öğretmen
Did you understand how a relation qualifies as a function?
06:44:15
Öğrenci
I got it
06:44:17
💭 AI Öğretmen
Let us review the question next
06:44:17
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:44:41
Öğrenci
My answer is: 18
06:44:42
💭 AI Öğretmen
Noted your answer.
06:44:47
AI Öğretmen
Fantastic job! You've correctly found the value of $f(3)$!
06:44:48
AI Öğretmen
You understood that to find $f(3)$, you needed to set $x - 1 = 3$, which means $x$ must be $4$.
06:44:51
AI Öğretmen
Then, by substituting $x=4$ into the expression $4x + 2$, you correctly calculated $4(4) + 2 = 16 + 2 = 18$.
06:44:52
AI Öğretmen
This shows a great understanding of function evaluation and substitution!
06:44:52
AI Öğretmen
Therefore, the correct answer is 18.
06:44:52
AI Öğretmen
Should we continue with the lecture?
06:45:30
Öğrenci
Alright, let's continue
06:45:31
💭 AI Öğretmen
Let us proceed further
06:45:41
AI Öğretmen
In this lesson, we covered the definition of a function as a relation where every input from the domain maps to exactly one output in the codomain. We also discussed the concepts of domain, codomain, and range, and explored how to determine if a relation is a function by checking that each input has a unique output. Additionally, we looked at examples illustrating these ideas. Do you have any questions about these topics? If not, we can wrap up the lesson.

Voltran Okul Analiz Sistemi