Oturum Detayları - 30140ac9-babb-4194-a17f-ed7f03dcb669

Oturum Bilgileri

Başlangıç

02 December 2025, 05:15

Bitiş

Devam ediyor

Süre

10 dakika

Durum

Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:

Introduction to Functions and Linear Functions

Alt Konular:

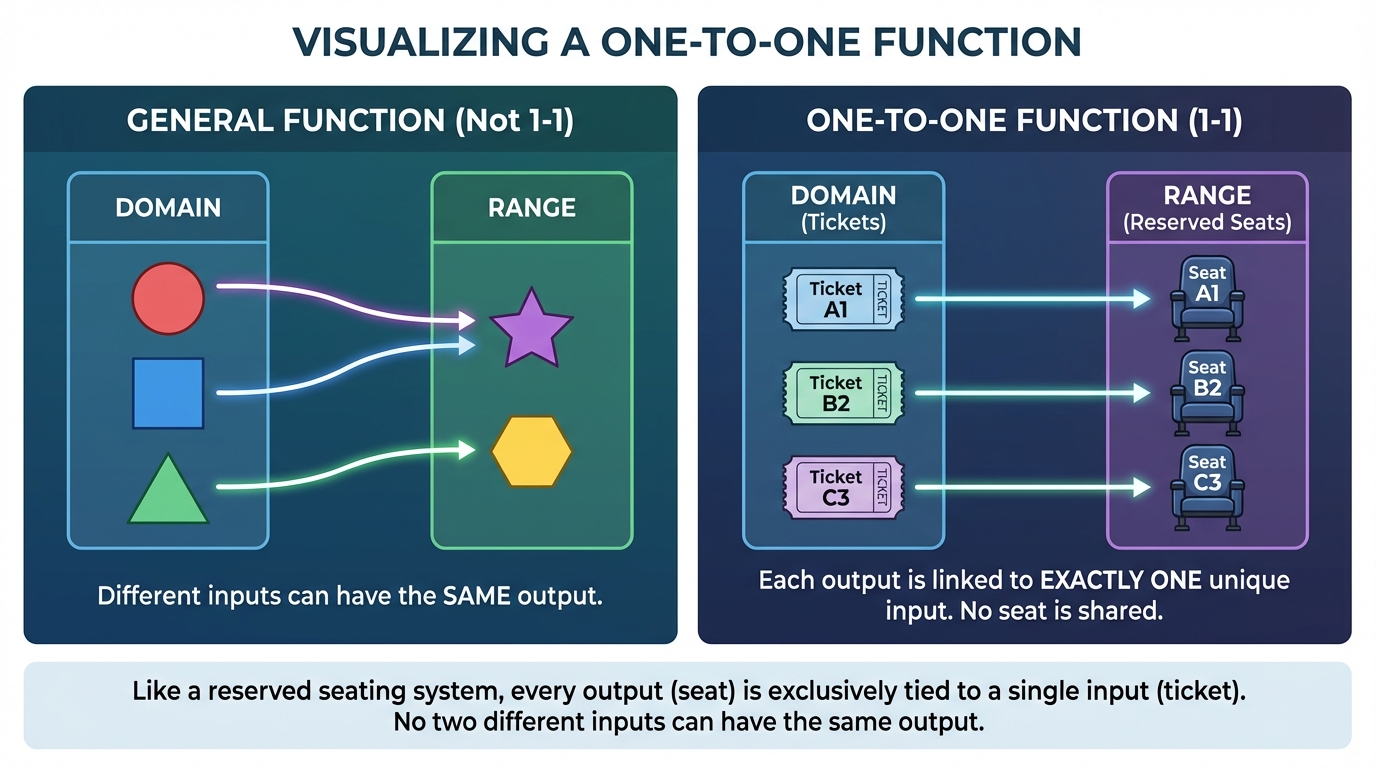
2.1.d. One to One Function

Detaylı Değerlendirme

Öğrenci Performans Analizi

Öğrenci, "Bire Bir Fonksiyon" (One to One Function) konusuna bir açıklama isteyerek başladı. İlk teorik açıklamadan sonra konuyu anladığını belirtse de, kendisine yöneltilen ilk soruda (bir şema üzerinden fonksiyonun bire bir olup olmadığını belirleme) yanlış cevap verdi. Bu durum, öğrencinin konunun tanımını görsel veya şematik temelde yorumlamakta zorlandığını göstermektedir.

AI öğretmenin detaylı açıklamasının ardından, öğrenci ikinci soruda (doğrusal bir fonksiyon olan f(x) = 5x - 9'un bire bir olup olmadığını belirleme) doğru cevap verdi. Bu, öğrencinin konuyu cebirsel olarak anladığını ancak kavramsal ve görsel yorumlamada eksiklikleri olabileceğini düşündürmektedir.

Özetle:
- Öğrencinin konunun temel tanımını ve görsel temsilini anlamasında boşluklar bulunmaktadır.
- İlk yanlış cevabından sonra verilen ek açıklamalarla konuyu daha iyi kavramış ve ikinci soruyu doğru yanıtlamıştır.
- Performansı karmaşık olduğu için, konunun tam olarak pekiştirildiği söylenemez ve eksiklikler listesine eklenmesi daha uygundur.

📜 Oturum Detayları

05:15:14

Öğrenci

Yes, I am ready! Can you explain this topic in detail?

05:15:15

💭 AI Öğretmen

Certainly, preparing explanation now

05:15:15

Görsel

Görsel

05:15:18

AI Öğretmen

A one-to-one function, also called a 1-1 function, is a special type of function where each output value comes from exactly one unique input value.

05:15:20

AI Öğretmen

This means that if you pick two different input values, you will always get two different output values.

05:15:23

AI Öğretmen

In a general function, it is possible for different inputs to give the same output, but in a one-to-one function, this is not allowed.

05:15:25

AI Öğretmen

You can imagine this like a reserved seating system at a movie theater, where each ticket matches one specific seat, and no two tickets are for the same seat.

05:15:27

AI Öğretmen

In terms of functions, every output is linked to only one input, so each output is the result of at most one input from the domain.

05:15:28

AI Öğretmen

Did you understand how a one-to-one function works?

05:16:38

Öğrenci

I got it

05:16:41

💭 AI Öğretmen

Let us review this first

05:16:41

❓ Soru basic

Determine whether the following function is one-to-one: ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_185ba90c-a01e-449e-9b2f-98a502915e79.png)

05:19:33

Öğrenci

My answer is: yes

05:19:34

💭 AI Öğretmen

Let me review your answer

05:19:37

AI Öğretmen

Your answer was not correct, let me explain why the function is not one-to-one.

05:19:39

AI Öğretmen

A function is one-to-one if every element in the domain maps to a unique element in the codomain, meaning no two different inputs share the same output.

05:19:41

AI Öğretmen

In the diagram, both inputs \(b\) and \(c\) map to the same output \(y\), which means two different inputs have the same output. This breaks the rule for one-to-one functions.

05:19:42

AI Öğretmen

A common mistake is thinking that as long as each input has an output, the function is one-to-one, but the key is that outputs must be unique for each input.

05:19:44

AI Öğretmen

For example, if \(f(a) = x\), \(f(b) = y\), and \(f(c) = y\), then \(f\) is not one-to-one because \(b \neq c\) but \(f(b) = f(c)\).

05:19:45

AI Öğretmen

Therefore, the correct answer should be that the function is not one-to-one.

05:19:45

AI Öğretmen

Should we continue with the lecture?

05:22:41

Öğrenci

Alright, let's continue

05:22:42

💭 AI Öğretmen

Moving forward now

05:22:46

🎥 Video

05:22:47

AI Öğretmen

Did this explanation make the concept of one-to-one functions clear to you?

05:23:16

Öğrenci

I got it

05:23:18

💭 AI Öğretmen

Let us proceed now

05:23:18

❓ Soru basic

**Example:** Determine whether the function $f: \mathbb{R} \to \mathbb{R}, f(x) = 5x - 9$ is one to one or not. Explain your reasoning.

05:23:42

Öğrenci

My answer is: it is

05:23:43

💭 AI Öğretmen

Let me review your answer

05:23:47

AI Öğretmen

That's absolutely right! You've correctly identified that the function is one-to-one.

05:23:48

AI Öğretmen

Great job! A linear function like $f(x) = 5x - 9$ with a non-zero slope will always be one-to-one because each input $x$ maps to a unique output $f(x)$.

05:23:50

AI Öğretmen

This means that if $f(x_1) = f(x_2)$, then $x_1$ must equal $x_2$, which is the key characteristic of a one-to-one function.

05:23:51

AI Öğretmen

Therefore, the correct answer is: The function is one-to-one.

05:23:52

AI Öğretmen

Should we continue with the lecture?

05:24:21

Öğrenci

Alright, let's continue

05:24:22

💭 AI Öğretmen

Moving forward now

05:24:29

🎥 Video

05:24:30

AI Öğretmen

Did you understand the difference between the one-to-one relationship using fingerprints and the example with birth months?

05:25:04

Öğrenci

I got it

05:25:07

💭 AI Öğretmen

Now let's review this question

05:25:07

❓ Soru basic

![image](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_8d6b21fc-51d8-4a5e-a89c-b6f20bfc4400.png) Let $A = \{1,2,3,4\}$ and $B = \{a, b, c, d\}$. Determine whether the function shown in diagram is one-to-one.