← Ana Rapor / Yaman Arhan KOCA / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
02 December 2025, 06:27
Bitiş
02 December 2025, 06:46
Süre
18 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Introduction to Functions and Linear Functions
Alt Konular:
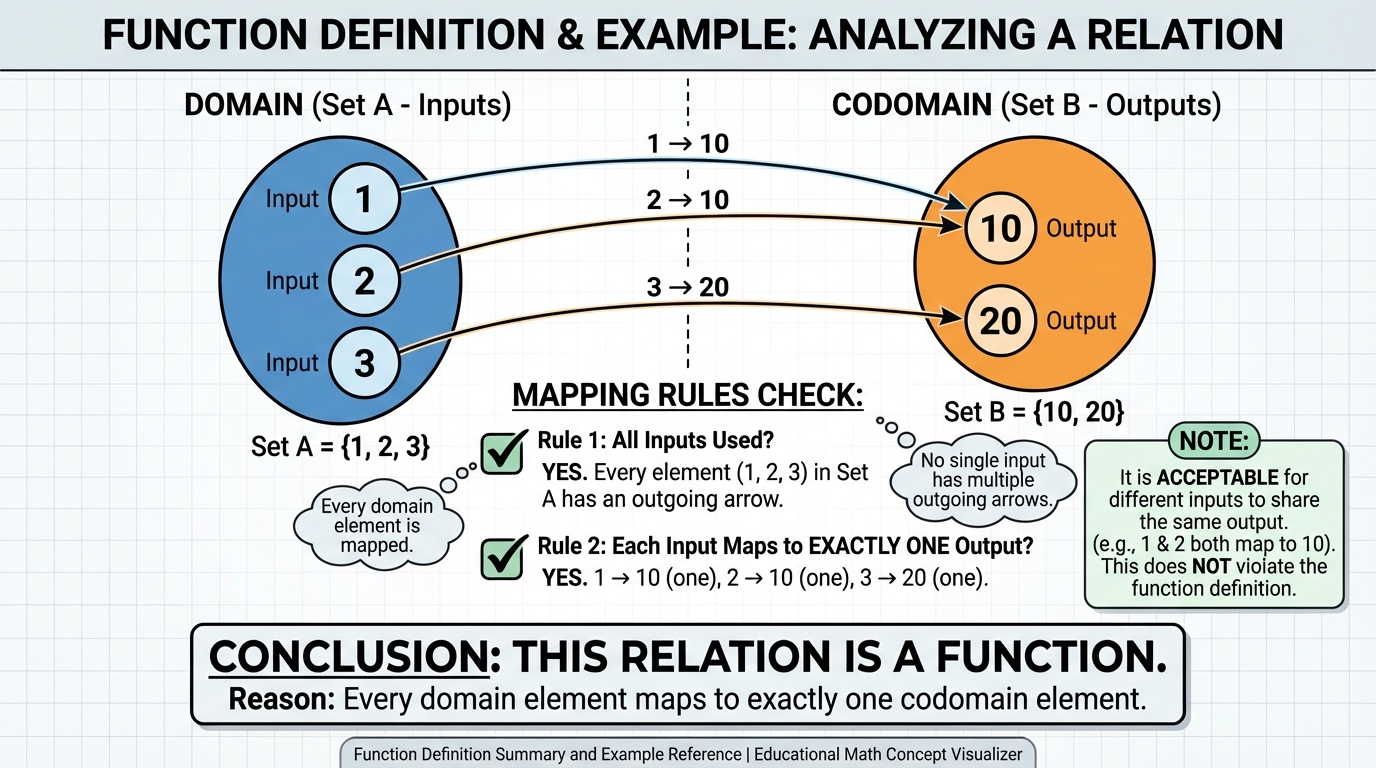
  • 2.1.a. Formal Definitions of Functions

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci, fonksiyonların temel tanımları konusunda genel olarak iyi bir anlama seviyesi göstermiştir. Özellikle bir fonksiyonun tanım kümesi (domain), değer kümesi (codomain) ve görüntü kümesini (range) tanımlama ve verilen bir diyagramdan bunları doğru bir şekilde bulma konusunda başarılıdır. Ayrıca, bir bağıntının fonksiyon olup olmadığını belirleme kriterlerini (örneğin, tanım kümesindeki her elemanın değer kümesinde bir karşılığı olması gerektiği) doğru bir şekilde uygulayabilmektedir. Rasyonel bir fonksiyonun en geniş tanım kümesini bulma konusunda da yetkinlik göstermiştir.

Ancak, dersin sonlarına doğru karşılaşılan ve fonksiyonun argümanının değiştirildiği (örneğin, f(x) yerine f(x-1) verildiğinde f(3)'ü bulma) bir soruda zorlanmış ve ipucu istemiştir. Bu durum, fonksiyonlarda değer bulma ve değişken değiştirme konularında pratik eksiği olduğunu göstermektedir. İpucu verildikten sonra soruyu doğru çözmesi, konunun temelini anladığını ancak daha karmaşık uygulamalarda desteğe ihtiyaç duyduğunu göstermektedir.

Güçlü Yönler
- Temel Kavramlar: Tanım kümesi, değer kümesi ve görüntü kümesi gibi temel fonksiyon kavramlarını doğru bir şekilde tanımlayıp uygulayabilmektedir.
- Fonksiyon Olma Şartları: Bir bağıntının fonksiyon olup olmadığını belirleme konusunda başarılıdır. Özellikle tanım ve değer kümesi arasındaki ilişkiyi doğru yorumlamıştır.
- Tanım Kümesi Bulma: Paydayı sıfır yapan değeri bularak rasyonel bir fonksiyonun en geniş tanım kümesini doğru bir şekilde belirlemiştir.

Geliştirilmesi Gereken Yönler
- Fonksiyonlarda Değer Bulma: Fonksiyonun argümanı üzerinde işlem yapılması gereken (örn: f(x-1) gibi) daha karmaşık fonksiyon değerlendirme sorularında zorlanmaktadır. Bu konuyu pekiştirmek için daha fazla alıştırma yapması faydalı olacaktır.

Ders Dışı Konuşmalar
- Ders sırasında konu dışı herhangi bir yorum veya soru kaydedilmemiştir.

📜 Oturum Detayları

06:28:03
Öğrenci
Yes, I am ready! Can you explain this topic in detail?
06:28:03
💭 AI Öğretmen
Great, preparing explanation now
06:28:03
🎥 Video
06:28:04
AI Öğretmen
Did you understand how a function uniquely pairs elements from one set to another?
06:28:53
Öğrenci
I got it
06:28:54
💭 AI Öğretmen
Let us continue then
06:28:55
🎥 Video
06:28:56
AI Öğretmen
Does the explanation about domain, codomain, and range make sense to you?
06:29:32
Öğrenci
I got it
06:29:35
💭 AI Öğretmen
Let us continue now
06:29:35
❓ Soru basic
Example: Find the domain, codomain and range of the function f given below. ![Figure](https://pajxpzsolirfrzhpksii.supabase.co/storage/v1/object/public/question-images/question_f6a74df9-7314-44bf-a5ac-08e8a317e622.png) $f: A \rightarrow B$ Domain: Codomain: Range:
06:32:40
Öğrenci
My answer is: domain: -1, 0, 1, 2 codomain: 0,1,2,3,4,5 range 0,1,4
06:32:42
💭 AI Öğretmen
Let me review that answer
06:32:46
AI Öğretmen
Fantastic job! You've correctly identified the domain, codomain, and range of the function!
06:32:48
AI Öğretmen
Your understanding of how to interpret these sets from a mapping diagram is spot on.
06:32:50
AI Öğretmen
Remember, the domain is all the inputs, the codomain is all possible outputs, and the range is the actual outputs that are mapped to. Keep up the great work!
06:32:52
AI Öğretmen
Therefore the correct answer is Domain: $\{-1, 0, 1, 2\}$, Codomain: $\{0, 1, 2, 3, 4, 5\}$, Range: $\{0, 1, 4\}$
06:32:52
AI Öğretmen
Should we continue with the lecture?
06:33:24
Öğrenci
Alright, let's continue
06:33:25
💭 AI Öğretmen
Proceeding with continuation
06:33:31
Görsel
Görsel
06:33:32
AI Öğretmen
A relation is called a function when it meets a specific rule.
06:33:33
AI Öğretmen
This rule is that every input, which comes from the domain (Set A), has to be paired with an output from the codomain (Set B).
06:33:34
AI Öğretmen
It's important to know that not every element in the codomain needs to be matched, so having extra elements in the codomain that do not get used is allowed.
06:33:37
AI Öğretmen
More than one input can share the same output, which means many-to-one mappings are allowed in a function.
06:33:38
AI Öğretmen
However, a single input cannot have more than one output, so one-to-many mappings are not allowed.
06:33:39
AI Öğretmen
In summary, a function gives exactly one output in the codomain for each input from the domain.
06:33:39
AI Öğretmen
Did you understand how a function relates elements from the domain to the codomain?
06:34:15
Öğrenci
I got it
06:34:17
💭 AI Öğretmen
Let us reinforce this concept
06:34:18
❓ Soru basic
State whether the relation $f : \mathbb{N} \to \mathbb{N}$, where $f(x) = x - 3$, is a function on the given domain.
06:36:52
Öğrenci
My answer is: İt is not a function because for example if we take 1=x it will be negative which does not take the rules of a function into consideration because of the domain having to be a natural number.
06:36:53
💭 AI Öğretmen
Let me review that carefully
06:36:57
AI Öğretmen
That's absolutely right! You've nailed it!
06:36:59
AI Öğretmen
You correctly identified that for a relation to be a function, every input from the domain must produce an output that is part of the codomain.
06:37:00
AI Öğretmen
Your example with $x=1$ perfectly demonstrates that $f(1) = -2$, which is not a natural number, so it falls outside the specified codomain $\mathbb{N}$.
06:37:01
AI Öğretmen
Great job understanding how domain and codomain define whether a relation is a function!
06:37:02
AI Öğretmen
Therefore, the correct answer is No, it is not a function.
06:37:02
AI Öğretmen
Should we continue with the lecture?
06:37:30
Öğrenci
Alright, let's continue
06:37:31
💭 AI Öğretmen
Proceeding with the lecture
06:37:35
Görsel
Görsel
06:37:37
AI Öğretmen
A relation between two sets can be analyzed to determine if it is a function by checking specific rules.
06:37:39
AI Öğretmen
Consider two sets: Set A (Inputs) is $\{1, 2, 3\}$ and Set B (Outputs) is $\{10, 20\}$.
06:37:41
AI Öğretmen
The mappings are: $1 \to 10$, $2 \to 10$, $3 \to 20$.
06:37:43
AI Öğretmen
Each element 1, 2, and 3 from the input set is mapped (1 to 10, 2 to 10, 3 to 20), so all inputs are used, and each input is matched to only one output.
06:37:44
AI Öğretmen
It is allowed for different inputs to share the same output like 1 and 2 both mapping to 10.
06:37:46
AI Öğretmen
Conclusion: This relation is a function because every domain element maps to exactly one codomain element.
06:37:47
AI Öğretmen
Did you understand why the given relation is considered a function?
06:38:34
Öğrenci
I got it
06:38:36
💭 AI Öğretmen
Let's reinforce this concept
06:38:36
❓ Soru basic
Find the largest domain of the following function. $f(x) = \frac{4}{x+2}$
06:41:16
Öğrenci
My answer is: R - (-2)
06:41:18
💭 AI Öğretmen
Let me review that answer
06:41:23
AI Öğretmen
Fantastic job! You've correctly identified that the domain includes all real numbers except for the value that makes the denominator zero.
06:41:25
AI Öğretmen
This is a crucial concept for rational functions: we must always exclude any x-values that would lead to division by zero, as that makes the function undefined.
06:41:26
AI Öğretmen
Your understanding of how to find restrictions in a function's domain is excellent!
06:41:27
AI Öğretmen
Therefore, the correct answer is R - {-2}.
06:41:27
AI Öğretmen
Should we continue with the lecture?
06:41:56
Öğrenci
Alright, let's continue
06:41:57
💭 AI Öğretmen
Preparing the next part
06:42:07
AI Öğretmen
A relation is called a function when each input from the domain is matched with one and only one output in the codomain.
06:42:08
AI Öğretmen
This means that for every value you pick in the domain, you get a single, specific result in the codomain.
06:42:10
AI Öğretmen
However, it is okay if multiple inputs from the domain map to the same output in the codomain; shared outputs are allowed.
06:42:11
AI Öğretmen
The key point is that no input in the domain can have more than one output in a function.
06:42:13
AI Öğretmen
Does the concept of a function having exactly one output for each input make sense to you?
06:42:44
Öğrenci
I got it
06:42:46
💭 AI Öğretmen
Let's review this carefully
06:42:47
❓ Soru basic
Find the indicated value for the function given below. $f: \mathbb{R} \to \mathbb{R}, f(x - 1) = 4x + 2, f(3)=?$
06:43:36
Öğrenci
Can you give me a hint, teacher?
06:43:37
💭 AI Öğretmen
Let me consider that
06:43:40
AI Öğretmen
What does the expression \( f(x-1) = 4x + 2 \) tell you about how the function \( f \) behaves when its input is \( x-1 \)?
06:43:41
AI Öğretmen
If you want to find \( f(3) \), what value of \( x \) would make the input \( x - 1 \) equal to 3?
06:43:44
AI Öğretmen
Once you find that \( x \), how can you use the expression \( f(x-1) = 4x + 2 \) to calculate \( f(3) \)?
06:44:29
Öğrenci
My answer is: 18
06:44:30
💭 AI Öğretmen
Let me review that
06:44:36
AI Öğretmen
That's absolutely right! Fantastic job!
06:44:38
AI Öğretmen
You correctly set $x - 1$ equal to 3 to find the value of $x$ that makes the argument 3.
06:44:39
AI Öğretmen
Then, by substituting $x=4$ into the expression $4x+2$, you accurately calculated $f(3)$. This shows a great understanding of function evaluation!
06:44:40
AI Öğretmen
Therefore, the correct answer is 18.
06:44:40
AI Öğretmen
Should we continue with the lecture?
06:45:13
Öğrenci
Alright, let's continue
06:45:13
💭 AI Öğretmen
Continuing with the lesson
06:45:25
AI Öğretmen
In this lesson, we covered the definition of a function as a relation where each input from the domain maps to exactly one output in the codomain. We also discussed the concepts of domain, codomain, and range, and how to determine if a relation is a function by checking these mappings. Examples were given to illustrate these ideas, including how multiple inputs can share the same output but no input can have multiple outputs. Do you have any questions about these topics? If not, we can wrap up the lesson.
06:46:20
Öğrenci
we can wrap up the lesson
06:46:25
AI Öğretmen
See you in the next lesson!

Voltran Okul Analiz Sistemi